Типовые статические нагрузки электропривода

Кинематическая схема электропривода

Непосредственное представление о механических связях даёт кинематическая схема электропривода (рис. 2.2):

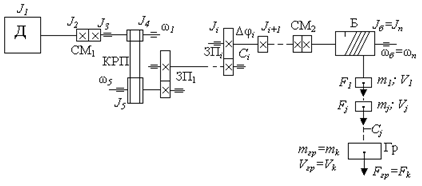
Рис. 2.2. Кинематическая схема электропривода

Здесь двигатель Д через соединительную муфту СМ₁, клиноременную передачу (КРП), ряд зубчатых передач ЗП_i и соединительную муфту СМ₂ приводит во вращение барабан (Б), преобразующий вращательное движение в поступательное движение ряда связанных масс. При нагружении элементы системы (валы, опоры, клиноременные передачи, зубчатые зацепления и т.п.) деформируются, т. к. механические связи не являются абсолютно жёсткими. При изменении нагрузки массы имеют возможность взаимного перемещения, которое определяется жёсткостью связи.

Каждый вращательно движущийся элемент обладает моментом инерции J_i и связан с (i +1) - элементом механической связью, обладающей жёсткостью C _i. Соответственно каждый поступательно движущийся элемент имеет массу m_j и связан со следующим связью с жёсткостью С_j. В пределах механических связей, для которых выполняется закон Гука, жёсткости можно определить с помощью соотношений

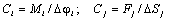(2.1)

где

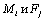- нагрузка упругой механической связи;

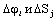- деформация упругого элемента при вращательном и поступательном движении.

В связи с наличием передач различные элементы системы движутся с различными скоростями. Поэтому для составления расчетных схем необходимо приведение всех параметров элементов кинематической цепи к одной расчётной скорости, обычно к скорости вала двигателя.

Условием соответствия расчётной схемы реальной механической системе является выполнение закона сохранения энергии. При приведении необходимо обеспечить сохранение кинетической и потенциальной энергий системы, а также элементарной работы всех действующих в системе сил и моментов на возможных перемещениях. Следовательно,

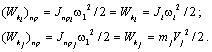(2.2)

Отсюда получаем формулы приведения:

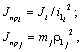(2.3)

где

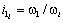- передаточное число от вала приведения до i -го вала;

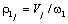- радиус приведения к валу со скоростью ω 1.

При приведении вращательных φ _i и поступательных S_j перемещений необходимо учитывать, что передаточное число и радиус приведения определяются соотношением скоростей. Тогда перемещения связаны зависимостями:

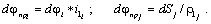
При линейных кинематических связях 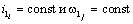. В этом случае формулы приведения перемещений имеют вид:

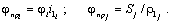
При приведении жёсткостей механических связей должно выполняться условие равенства запаса потенциальной энергии деформации.

Потенциальная энергия W_n равна работе, совершаемой моментом М на участке изменения угла Δφ. Так как величина момента скручивания изменяется от 0 до M_max, то, с учетом (2.1), работа равна:

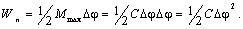
Тогда

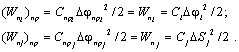
Формулы приведения:

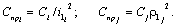(2.4)

Приведение моментов и сил нагрузки элементов кинематической цепи должно осуществляться при условии равенства элементарной работы на возможных перемещениях:

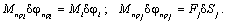
Следовательно,

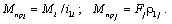(2.5)

Для большей наглядности сопоставления по результатам приведения можно построить исходную приведённую расчётную схему, представив в ней массы в виде прямоугольников, площадь которых пропорциональна приведенным моментам инерции, а жёсткости связей между ними в виде соединений, длина которых обратно пропорциональна жёсткости.

Для рассматриваемой кинематической схемы приведённая расчётная схема имеет вид (рис. 2. 3):

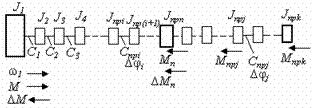
Рис. 2.3. Приведённая расчётная схема кинематической цепи.

В ней выделены три наиболее значительные массы – ротор двигателя с моментом инерции 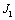, барабан с приведённым моментом инерции 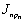и груз 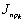. Вследствие относительно малых величин остальных моментов её можно существенно упростить. Для этого следует малые массы добавить к близлежащим большим, а затем определить эквивалентные жёсткости связей между полученными массами по общей формуле:

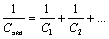(2.6)

К ротору двигателя с моментом инерции приложен электромагнитный момент М и момент потерь Δ М, причём для правильного учёта знаков действующих моментов указано положительное для всей приведённой схемы направление скорости ω 1.

Исследования динамики электропривода показывают, что неразветвлённые расчётные механические схемы в большинстве случаев сводятся к трёхмассовой (рис. 2.4а), двухмассовой (рис. 2.4б) расчётным схемам и к жёсткому приведённому механическому звену (рис. 2.4в):

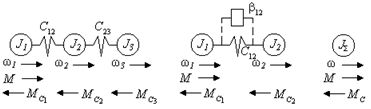
а) б) в)

Рис. 2.4. Расчётные схемы электропривода: трёхмассовая (б) и жёсткое приведённое механическое звено (в).

Трёхмассовая упругая система используется в тех случаях, когда необходимо более детально анализировать движения масс механизма. При этом обычно используется моделирование на аналоговой (ABM) или цифровой (ЦВМ) вычислительных машинах. Для исследования отдельных физических особенностей используется двухмассовая система.

В тех случаях, когда параметры системы таковы, что влияние упругих связей незначительно, или когда этим влиянием можно пренебречь, используется жёсткое приведённое звено. Суммарный приведённый момент инерции может быть выражен:

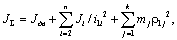(2.7)

где

n и k – число масс установки, совершающих соответственно вращательное и поступательное движение.

Суммарный приведённый к валу двигателя момент статической нагрузки M _C

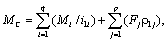(2.8)

где

q и p – число внешних моментов M_i и сил 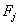, приложенных к системе, кроме электромагнитного момента двигателя.

Характерным примером разветвлённых кинематических схем является кинематическая схема многодвигательного электропривода, в котором двигатели через индивидуальные редукторы действуют на общий рабочий механизм.

Кроме электромагнитного момента на механическую часть электропривода действуют статические нагрузки, которые делятся на силы и моменты механических потерь и силы и моменты полезных нагрузок исполнительных механизмов:

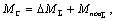(2.9)

где первая составляющая суммы является суммарными потерями в двигателе и в исполнительном механизме, а вторая – суммарным приведённым моментом полезной нагрузки.

По характеру взаимодействия с электроприводом различаются активные и реактивные силы и моменты.

Активными силами и моментами называются силы и моменты, величина и направление которых не зависит от движения электропривода; например, силы и моменты, создаваемые перемещаемым по вертикали грузом. Механическая характеристика такого вида статической активной нагрузки изображена на рис. 2.5.

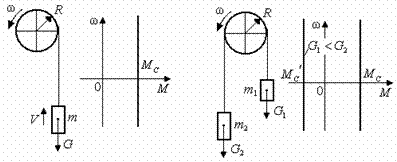
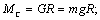
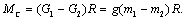
a) б)

Рис. 2.5. Активные нагрузки электропривода неуравновешенного (а) и уравновешенного (б) подъемных механизмов.

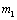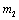В зависимости от соотношения масс и двигатель работает в тормозном () или двигательном (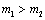) режимах.

Силы и моменты, возникающие как реакции на движение электропривода, называются реактивными. Направление их всегда противоположно направлению движению электропривода. По характеру зависимости от скорости реактивных сил и моментов различают нагрузки типов сухого трения (рис. 2.6):

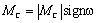
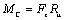
a) б)

Рис. 2.6. Реактивные нагрузки: сухое трение (а) и момент резания (б).

В момент трогания силы сухого трения могут превышать свои значения при движении (рис. 2.6а).

Силы и моменты вязкого трения зависят от скорости линейно (рис. 2.7):

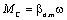(2.10)

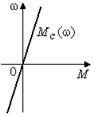
Рис. 2.7. Момент нагрузки типа вязкого трения.

Момент внутреннего вязкого трения:

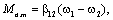(2.11)

где

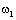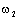и – скорости на входе и выходе деформируемого элемента.

По характеру влияния на механические колебания все силы и моменты делятся на консервативные и диссипативные.

При действии консервативных сил и моментов не происходит поглощение колебаний. Например, сила тяжести является консервативной силой, т. к. работа, осуществляемая этой силой за период колебаний, всегда равна нулю.

При действии диссипативных сил происходит поглощение энергии колебаний. Примером является вязкое трение, т.к. при изменении знака скорости изменяется и знак момента, а механическая мощность 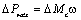сохраняет положительный знак, что соответствует поглощению колебаний.

На практике распространённой является вентиляторная нагрузка (рис. 2.8):

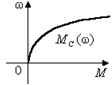
Рис. 2.8. Зависимость момента от скорости при вентиляторной нагрузке

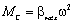(2.12)

Коэффициент полезного действия (КПД) механизма: η _мех =η₁η₂η₃.., где η₁, η₂, η₃ – КПД элементов кинематической цепи.

Если известен полезный момент нагрузки механизма M_мех, то для прямого направления энергии приведённый к валу двигателя момент статической нагрузки можно определить из равенства:

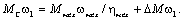
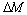( – момент механических потерь в двигателе.)

Следовательно,

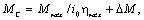(2.13)

где

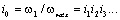- общее передаточное число от двигателя к рабочему органу механизма.

При обратном направлении потока энергии, когда нагрузка является активной и двигатель должен работать в тормозном режиме, уравнение баланса мощностей можно записать как:

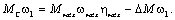
В этом случае

(2.14)

Момент механических потерь в двигателе невелик, он составляет 1-5% номинального момента двигателя. Во многих практических случаях полагают 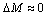, т.к. точность определения момента M_мех невелика и он рассчитывается с некоторым запасом. При этом формулы приведения момента статической нагрузки к валу двигателя принимают вид:

- для прямого направления передачи энергии (двигательный режим работы)

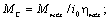(2.15)

- для обратного направления (тормозной режим работы)

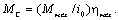(2.16)

Если рабочий орган движется поступательно, то уравнение баланса мощностей имеет вид (Δ М =0):

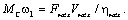
Тогда

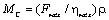(2.17)

Соответственно для обратного направления потока механической энергии

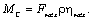(2.18)

Необходимо иметь в виду, что КПД передач зависит от нагрузки, а для червячного зацепления – и от направления передачи энергии, поэтому при расчётах следует использовать соответствующие зависимости η от полезной нагрузки передач.

Дата добавления: 2014-12-08