Резонанс токов

Лекция 19

Этот вид резонанса имеет место в схеме,образованной двумя параллельными ветвями с реактивными сопротивлениями разного характера.

İ

I_L

I_R I_C

U_вх C

L

R

R₁ L

İ R₂ C

Определим комплексную проводимость схемы а)

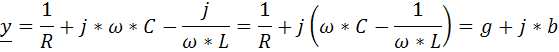
Используя проводимость найдём ток цепи:

İ= * =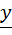

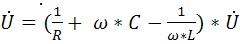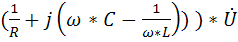
Для того чтобы в цепи был резонанс,т.е. чтобы ток и напряжение совпадали по фазе, необходимо чтобы реактивная составляющая проводимости j*b равнялась 0:

b= 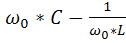=0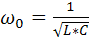

т.е резонансная частота определяется так же как при резонансе напряжений.

Действующее значение тока определим по формуле:

I=U*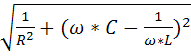

Получается,что при резонансе ток минимальный и равен I₀= .При частоте отличной от резонансной появляется реактивная составляющая проводимости b и ток увеличивается.

График зависимости тока параллельного резонансного контура от частоты показан на следующем рисунке:

Добротность при резонансе токов определяется как отношение реактивной проводимости(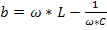) к активной проводимости (g= )

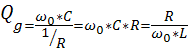
Добротность параллельного резонансного контура показывает во сколько раз ток,протекающий через реактивные элементы превышает ток на входе цепи.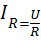

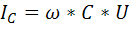
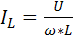
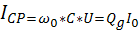
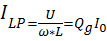
Если рассмотреть идеальный случай,когда R=∞,то ток при резонансе на входе цепи будет равен нулю,в то время,как в параллельных плечах схемы будут течь вполне реальные токи.

Постоим векторную диаграмму для контура изображённого на рисунке а) для трёх частот: 1 ω<ω₀ 2 ω=ω₀ 3 ω>ω₀

Построим векторную диаграмму для схемы б) в случае резонанса: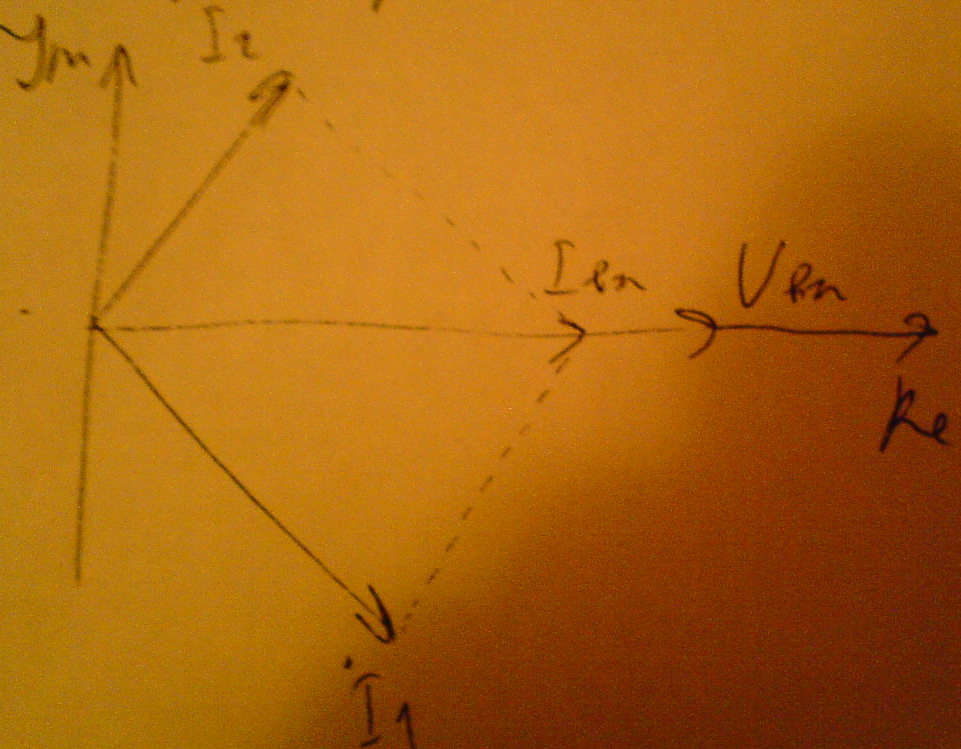

Определим входное сопротивление контура: –

-j 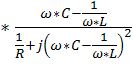=Rэкв+j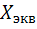

İ

U_ВХ C L

Для анализа рассмотрим идеальный контур,не содержащий активного сопротивления

Тогда его входное сопротивление будет равно:

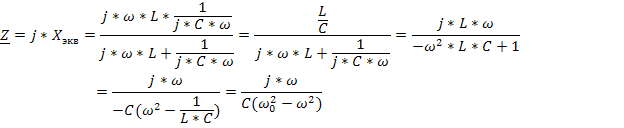
Построим частотную характеристику данного контура:

При ω→0 то Х_экв→0

При ω→ω₀ ,но ω<ω₀ то Х_экв→

При ω→ω_0, но ω>ω₀ то Х_экв→-

При ω→ , Х_экв→-0

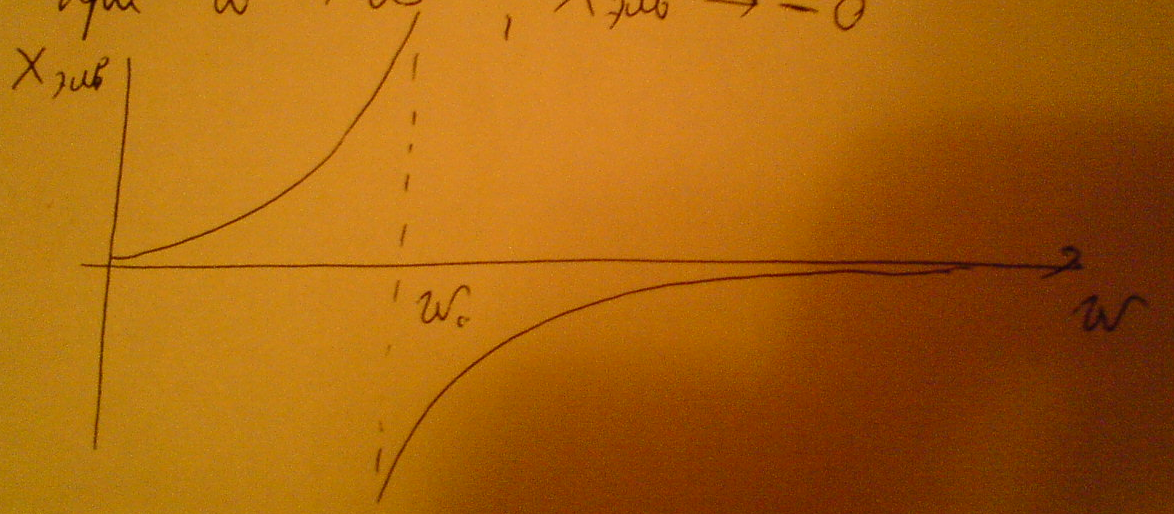
Дата добавления: 2014-12-08