Частотная характеристика сложного двухполюсника

Лекция 20

Входное сопротивление двухполюсника и его входная проводимость есть функции частоты.Зависимости действительной и мнимой частей входного сопротивления или входной проводимости двухполюсника от частоты называют частотными характеристиками двухполюсника.

В том случае,когда цепь содержит более 2х реактивных элементов,входное напряжение может совпадать по фазе с входным током на нескольких частотах.

R L₂ C₁

L₁

Это возможно когда два элемента (L₁ и C₁) образуют резонанс токов на частоте ω₀₁= 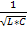.Сопротивление контура равно ∞ (проводимость равна 0).

Второй резонанс на частоте ω₀₂ наступает когда контур L₁C₁ имеет реактивное сопротивление ёмкостного характера,которое вместе с L₂ образует резонанс напряжений, при котором реактивная составляющая входного сопротивления Х равна 0.

X=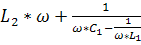

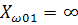
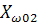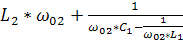=0= =0

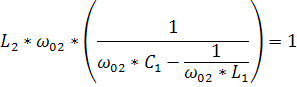
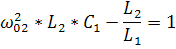
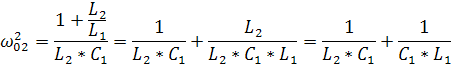
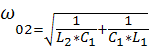
Полное суждения о свойствах такого двухполюсника можно получить если рассматривать его полное сопротивление как функцию частоты.Чаще эту зависимость разбивают на две: активную и реактивную.Для простоты анализа активным сопротивлением часто пренебрегают (R=0).Такой двухполюсник называется реактивным.С частотными характеристиками последовательного и параллельного контуров мы уже познакомились.

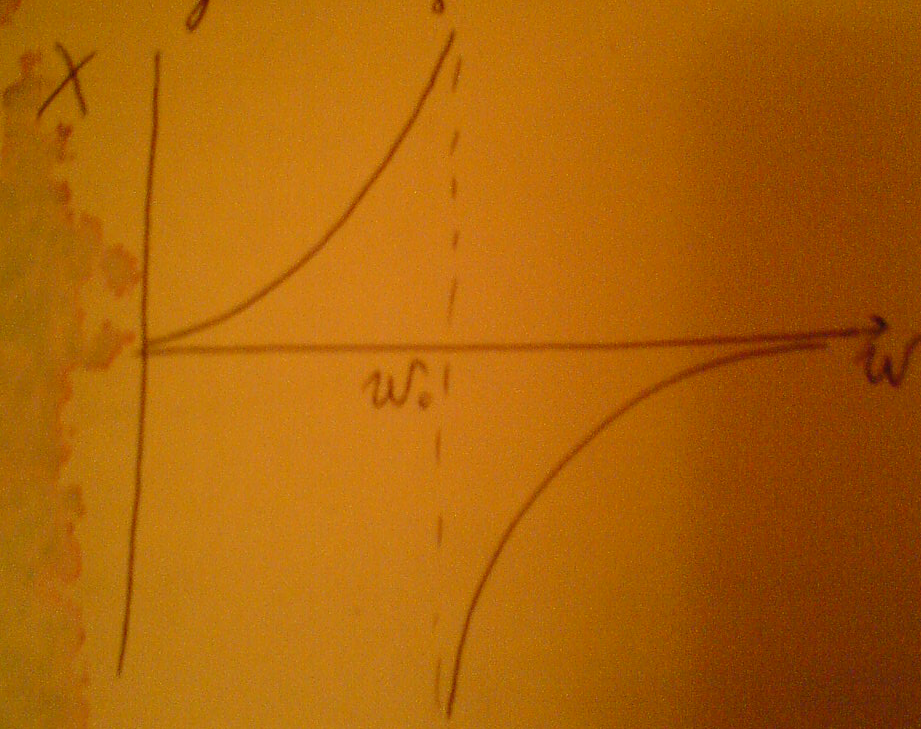
Построим частотную зависимость реактивной составляющей входного сопротивления для нашей схемы. C₁

L₂

L₁

X=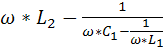

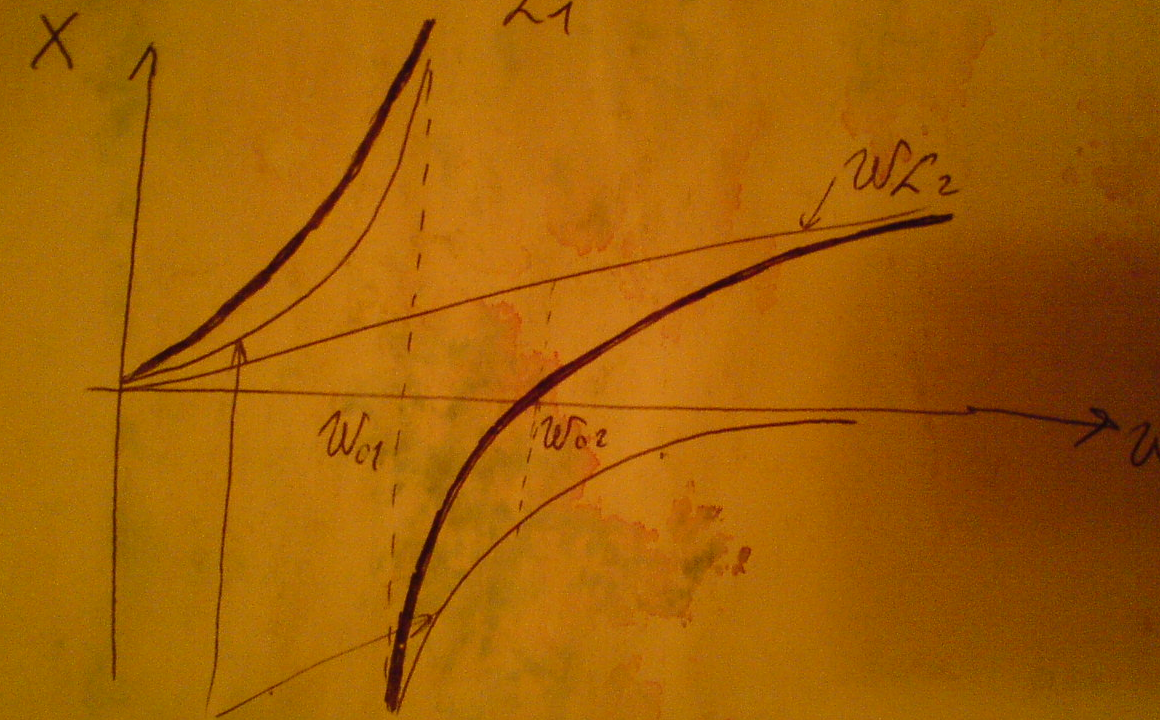
Резонансная частота параллельного участка ω₀₁ (резонанс токов) соответствует полюсу функции,а резонанс напряжений –соответствует нулю функции. Таким образом мы имеем два резонанса:резонанс токов и резонанс напряжений.Как видно из графика функция Х(ω) всегда возрастает,т.е 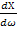>0.Из этого следует что не может быть двух подряд резонансов тока или резонанса напряжения,т.е резонансы чередуются.

Для того,чтобы построить качественно частотную характеристику достаточно определить откуда начинается характеристика при ω=0,куда стремится характеристика при ω→ 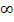и сколько резонансов она имеет.

L₁ C₁

L₂

C₂

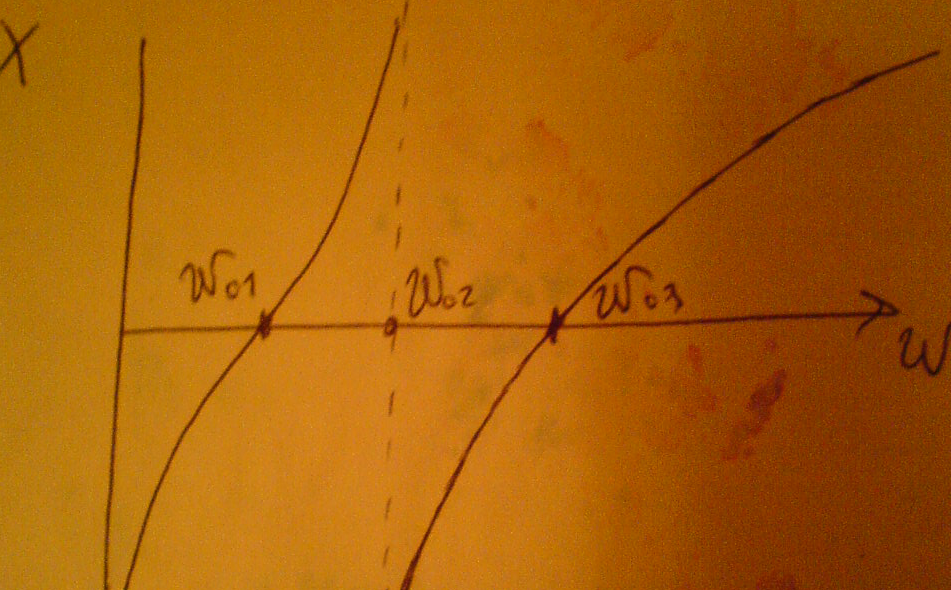
При ω→ 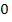,Х→-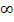

L₁ C₁

L₁

C₂

При ω→ Х→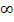

L₁ C₁

L₂

C₂

Если постоянный ток не проходит,то характеристика начинается из - 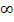,в противном случае из 0.Для того чтобы определить число резонансов электрическая схема должна быть сведена к канонической схеме,т.е параллельно или последовательно включенные однотипные реактивные элементы должны быть заменены одним эквивалентным.

C₁ C_{2 →} C=C ₁ +C₂

X_L1 X _L2 X_L= X_L1 + X _L2

_→

Число резонансов в такой схеме на единицу меньше числа реактивных элементов канонической схемы.

Если в схеме есть путь для постоянного тока,то первым наступит резонанс токов,если такого пути нет –то первым наступает резонанс напряжений.

Если в схеме есть прямой путь через ёмкость,то входное сопротивление стремится к 0 при бесконечно большой частоте,если такого пути нет, то сопротивление стремится к бесконечности.

Дата добавления: 2014-12-08