
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Где -объём параллелепипеда, построенного на векторах , и . 1 страница
|
|
|
|
Для векторов 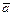 ,
, 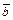 и
и 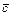 , заданных своими координатами
, заданных своими координатами 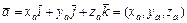 ,
, 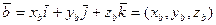 ,
, 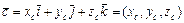 смешанное произведение вычисляется по формуле:
смешанное произведение вычисляется по формуле:  .
.
Смешанное произведение 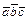 применяют: 1) для вычисления объёмов тетраэдра и параллелепипеда, построенных на векторах
применяют: 1) для вычисления объёмов тетраэдра и параллелепипеда, построенных на векторах 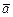 ,
, 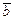 и
и 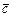 , как на рёбрах, по формуле:
, как на рёбрах, по формуле: 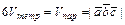 ; 2) в качестве условия компланарности векторов
; 2) в качестве условия компланарности векторов 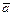 ,
, 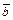 и
и 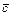 :
:  и
и 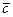 - компланарны.
- компланарны.
Тема 5. Прямые линии и плоскости.
Нормальным вектором прямой  , называется всякий ненулевой вектор
, называется всякий ненулевой вектор  перпендикулярный данной прямой. Направляющим вектором прямой
перпендикулярный данной прямой. Направляющим вектором прямой  , называется всякий ненулевой вектор
, называется всякий ненулевой вектор 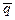 параллельный данной прямой.
параллельный данной прямой.
Прямая 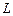 на плоскости в системе координат
на плоскости в системе координат 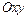 может быть задана уравнением одного из следующих видов:
может быть задана уравнением одного из следующих видов:
1)  - общее уравнение прямой, где
- общее уравнение прямой, где 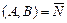 - нормальный вектор прямой;
- нормальный вектор прямой;
2)  - уравнение прямой, проходящей через точку
- уравнение прямой, проходящей через точку  перпендикулярно данному вектору
перпендикулярно данному вектору 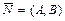 ;
;
3) 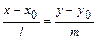 - уравнение прямой, проходящей через точку
- уравнение прямой, проходящей через точку  параллельно данному вектору
параллельно данному вектору  (каноническое уравнение);
(каноническое уравнение);
4) 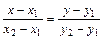 - уравнение прямой, проходящей через две данные точки
- уравнение прямой, проходящей через две данные точки 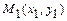 ,
,  ;
;
5) 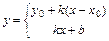 -уравнения прямой с угловым коэффициентом
-уравнения прямой с угловым коэффициентом 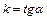 , где
, где  - точка через которую прямая проходит;
- точка через которую прямая проходит; 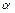 (
( ) – угол, который прямая составляет с осью
) – угол, который прямая составляет с осью  ;
; 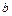 - длина отрезка (со знаком
- длина отрезка (со знаком 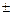 ), отсекаемого прямой на оси
), отсекаемого прямой на оси 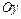 (знак «
(знак «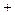 », если отрезок отсекается на положительной части оси и «
», если отрезок отсекается на положительной части оси и « », если на отрицательной).
», если на отрицательной).
6) 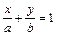 -уравнение прямой в отрезках, где
-уравнение прямой в отрезках, где  и
и 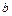 - длины отрезков (со знаком
- длины отрезков (со знаком 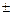 ), отсекаемых прямой на координатных осях
), отсекаемых прямой на координатных осях  и
и 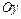 (знак «
(знак «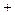 », если отрезок отсекается на положительной части оси и «
», если отрезок отсекается на положительной части оси и « », если на отрицательной).
», если на отрицательной).
Расстояние от точки  до прямой
до прямой  , заданной общим уравнением
, заданной общим уравнением 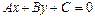 на плоскости, находится по формуле:
на плоскости, находится по формуле:
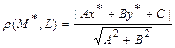 .
.
Угол 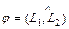 , (
, (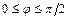 ) между прямыми
) между прямыми  и
и  , заданными общими уравнениями или уравнениями с угловым коэффициентом, находится по одной из следующих формул:
, заданными общими уравнениями или уравнениями с угловым коэффициентом, находится по одной из следующих формул:
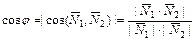 ;
; 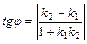 .
.
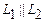 , если
, если 
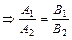 или
или 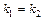 .
.
 ,если
,если 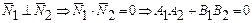 или
или 
Координаты точки пересечения прямых  и
и  находятся как решение системы линейных уравнений:
находятся как решение системы линейных уравнений: 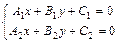 или
или 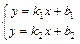 .
.
Нормальным вектором плоскости  , называется всякий ненулевой вектор
, называется всякий ненулевой вектор  перпендикулярный данной плоскости.
перпендикулярный данной плоскости.
Плоскость  в системе координат
в системе координат 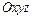 может быть задана уравнением одного из следующих видов:
может быть задана уравнением одного из следующих видов:
1)  - общее уравнение плоскости, где
- общее уравнение плоскости, где 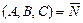 - нормальный вектор плоскости;
- нормальный вектор плоскости;
2) 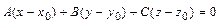 - уравнение плоскости, проходящей через точку
- уравнение плоскости, проходящей через точку 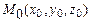 перпендикулярно данному вектору
перпендикулярно данному вектору 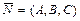 ;
;
3)  - уравнение плоскости, проходящей через три точки
- уравнение плоскости, проходящей через три точки 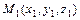 ,
, 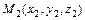 и
и 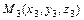 ;
;
4)  -уравнение плоскости в отрезках, где
-уравнение плоскости в отрезках, где  ,
, 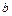 и
и 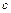 - дины отрезков (со знаком
- дины отрезков (со знаком 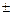 ), отсекаемых плоскостью на координатных осях
), отсекаемых плоскостью на координатных осях  ,
, 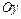 и
и 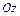 (знак «
(знак «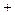 », если отрезок отсекается на положительной части оси и «
», если отрезок отсекается на положительной части оси и « », если на отрицательной).
», если на отрицательной).
Расстояние от точки 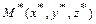 до плоскости
до плоскости  , заданной общим уравнением
, заданной общим уравнением 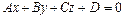 , находится по формуле:
, находится по формуле:
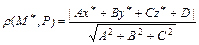 .
.
Угол  , (
, (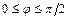 ) между плоскостями
) между плоскостями 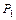 и
и  , заданными общими уравнениями, находится по формуле:
, заданными общими уравнениями, находится по формуле:
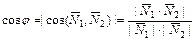 .
.
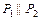 , если
, если 
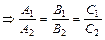
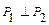 , если
, если  .
.
Прямая 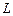 в пространстве в системе координат
в пространстве в системе координат 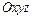 может быть задана уравнением одного из следующих видов:
может быть задана уравнением одного из следующих видов:
1)  - общее уравнение прямой, как линии пересечения двух плоскостей, где
- общее уравнение прямой, как линии пересечения двух плоскостей, где  и
и  - нормальные векторы плоскостей
- нормальные векторы плоскостей  и
и  ;
;
2) 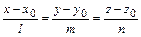 - уравнение прямой, проходящей через точку
- уравнение прямой, проходящей через точку 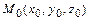 параллельно данному вектору
параллельно данному вектору 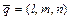 (каноническое уравнение);
(каноническое уравнение);
3) 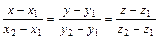 - уравнение прямой, проходящей через две данные точки
- уравнение прямой, проходящей через две данные точки 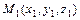 ,
, 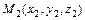 ;
;
4) 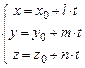 -уравнение прямой, проходящей через точку
-уравнение прямой, проходящей через точку 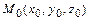 параллельно данному вектору
параллельно данному вектору  ,
, 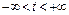 (параметрическое уравнение);
(параметрическое уравнение);
Угол 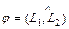 , (
, (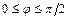 ) между прямыми
) между прямыми  и
и  в пространстве, заданными каноническими уравнениями находится по формуле:
в пространстве, заданными каноническими уравнениями находится по формуле:
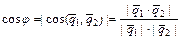 .
.
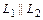 , если
, если 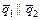
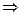
 .
.
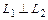 , если
, если  .
.
Координаты точки пересечения прямой  , заданной параметрическим уравнением и плоскости
, заданной параметрическим уравнением и плоскости  , заданной общим уравнением, находятся как решение системы линейных уравнений:
, заданной общим уравнением, находятся как решение системы линейных уравнений: 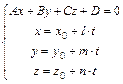 .
.
Угол 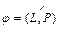 , (
, (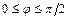 ) между прямой
) между прямой  , заданной каноническим уравнением и плоскостью
, заданной каноническим уравнением и плоскостью  , заданной общим уравнением находится по формуле:
, заданной общим уравнением находится по формуле: 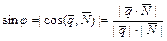 .
.
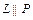 , если
, если 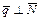
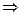

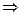
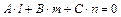 .
.
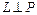 , если
, если 
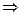
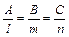 .
.
Тема 6. Кривые второго порядка.
Алгебраической кривой второго порядка в системе координат 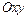 называется кривая
называется кривая  , общее уравнение которой имеет вид:
, общее уравнение которой имеет вид:
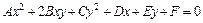 ,
,
где числа  - не равны нулю одновременно. Существует следующая классификация кривых второго порядка: 1) если
- не равны нулю одновременно. Существует следующая классификация кривых второго порядка: 1) если 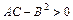 , то общее уравнение определяет кривую эллиптического типа (окружность (при
, то общее уравнение определяет кривую эллиптического типа (окружность (при  ), эллипс (при
), эллипс (при 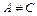 ), пустое множество, точку); 2) если
), пустое множество, точку); 2) если 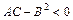 , то - кривую гиперболического типа (гиперболу, пару пересекающихся прямых); 3) если
, то - кривую гиперболического типа (гиперболу, пару пересекающихся прямых); 3) если  , то - кривую параболического типа (параболу, пустое множество, прямую, пару параллельных прямых). Окружность, эллипс, гипербола и парабола называются невырожденными кривыми второго порядка.
, то - кривую параболического типа (параболу, пустое множество, прямую, пару параллельных прямых). Окружность, эллипс, гипербола и парабола называются невырожденными кривыми второго порядка.
Общее уравнение  , где
, где 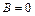 , определяющее невырожденную кривую (окружность, эллипс, гиперболу, параболу), всегда (методом выделения полных квадратов) можно привести к уравнению одного из следующих видов:
, определяющее невырожденную кривую (окружность, эллипс, гиперболу, параболу), всегда (методом выделения полных квадратов) можно привести к уравнению одного из следующих видов:
1а)  -уравнение окружности с центром в точке
-уравнение окружности с центром в точке 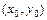 и радиусом
и радиусом  (рис. 5).
(рис. 5).
1б)  - уравнение эллипса с центром в точке
- уравнение эллипса с центром в точке  и осями симметрии, параллельными координатным осям. Числа
и осями симметрии, параллельными координатным осям. Числа 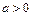 и
и  - называются полуосями эллипса; прямоугольник со сторонами
- называются полуосями эллипса; прямоугольник со сторонами  ,
, 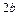 параллельными осям симметрии и центром в точке
параллельными осям симметрии и центром в точке 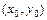 - основным прямоугольником эллипса; точки пересечения основного прямоугольника с осями симметрии - вершинами эллипса.
- основным прямоугольником эллипса; точки пересечения основного прямоугольника с осями симметрии - вершинами эллипса.
Для построения эллипса в системе координат 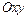 : 1) отмечаем центр
: 1) отмечаем центр  эллипса; 2) проводим через центр пунктирной линией оси симметрии эллипса; 3) строим пунктиром основной прямоугольник эллипса с центром
эллипса; 2) проводим через центр пунктирной линией оси симметрии эллипса; 3) строим пунктиром основной прямоугольник эллипса с центром  и сторонами
и сторонами  ,
, 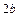 параллельными осям симметрии; 4) изображаем сплошной линией эллипс, вписывая его в основной прямоугольник так, чтобы эллипс касался его сторон только в вершинах эллипса (рис.6).
параллельными осям симметрии; 4) изображаем сплошной линией эллипс, вписывая его в основной прямоугольник так, чтобы эллипс касался его сторон только в вершинах эллипса (рис.6).
Аналогично строится и окружность, основной прямоугольник которой имеет стороны  (рис. 5).
(рис. 5).

Рис.5 Рис 6
2) 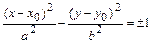 - уравнения гипербол (называемых сопряжёнными) с центром в точке
- уравнения гипербол (называемых сопряжёнными) с центром в точке  и осями симметрии, параллельными координатным осям. Числа
и осями симметрии, параллельными координатным осям. Числа 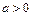 и
и  - называются полуосями гипербол; прямоугольник со сторонами
- называются полуосями гипербол; прямоугольник со сторонами  ,
, 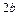 параллельными осям симметрии и центром в точке
параллельными осям симметрии и центром в точке 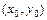 - основным прямоугольником гипербол; точки пересечения основного прямоугольника с осями симметрии - вершинами гипербол; прямые
- основным прямоугольником гипербол; точки пересечения основного прямоугольника с осями симметрии - вершинами гипербол; прямые 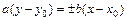 , проходящие через противоположные вершины основного прямоугольника – асимптотами гипербол.
, проходящие через противоположные вершины основного прямоугольника – асимптотами гипербол.
Для построения гиперболы в системе координат 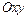 : 1) отмечаем центр гиперболы
: 1) отмечаем центр гиперболы  ; 2) проводим через центр
; 2) проводим через центр  пунктирной линией оси симметрии гиперболы; 3) строим пунктиром основной прямоугольник гиперболы с центром
пунктирной линией оси симметрии гиперболы; 3) строим пунктиром основной прямоугольник гиперболы с центром  и сторонами
и сторонами  и
и 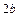 параллельными осям симметрии; 4) проводим через противоположные вершины основного прямоугольника пунктирной линией прямые, являющиеся асимптотами гиперболы, к которым неограниченно близко, при бесконечном удалении от начала координат, приближаются ветви гиперболы, не пересекая их; 5) изображаем сплошной линией ветви гиперболы
параллельными осям симметрии; 4) проводим через противоположные вершины основного прямоугольника пунктирной линией прямые, являющиеся асимптотами гиперболы, к которым неограниченно близко, при бесконечном удалении от начала координат, приближаются ветви гиперболы, не пересекая их; 5) изображаем сплошной линией ветви гиперболы 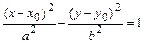 (рис. 7) или гиперболы
(рис. 7) или гиперболы  (рис. 8).
(рис. 8).

Рис.7 Рис.8
3а) 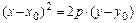 - уравнение параболы с вершиной в точке
- уравнение параболы с вершиной в точке  и осью симметрии, параллельной координатной оси
и осью симметрии, параллельной координатной оси 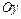 (рис. 9).
(рис. 9).
3б) 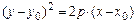 - уравнение параболы с вершиной в точке
- уравнение параболы с вершиной в точке  и осью симметрии, параллельной координатной оси
и осью симметрии, параллельной координатной оси  (рис. 10).
(рис. 10).
Для построения параболы в системе координат 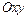 : 1) отмечаем вершину параболы
: 1) отмечаем вершину параболы  ; 2) проводим через вершину
; 2) проводим через вершину  пунктирной линией ось симметрии параболы; 3) изображаем сплошной линией параболу, направляя её ветвь, с учётом знака параметра параболы
пунктирной линией ось симметрии параболы; 3) изображаем сплошной линией параболу, направляя её ветвь, с учётом знака параметра параболы 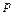 : при
: при 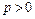 - в положительную сторону координатной оси, параллельной оси симметрии параболы (рис. 9а и 10а); при
- в положительную сторону координатной оси, параллельной оси симметрии параболы (рис. 9а и 10а); при 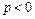 - в отрицательную сторону координатной оси (рис.9б и 10б).
- в отрицательную сторону координатной оси (рис.9б и 10б).

Рис. 9а Рис. 9б
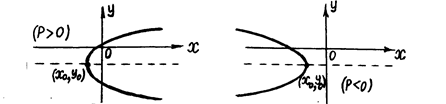
Рис. 10а Рис. 10б
Тема 7. Множества. Числовые множества. Функция.
Под множеством понимают некоторую совокупность объектов любой природы, различимых между собой и мыслимую как единое целое. Объекты, составляющие множество называют его элементами. Множество может быть бесконечным (состоит из бесконечного числа элементов), конечным (состоит из конечного числа элементов), пустым (не содержит ни одного элемента). Множества обозначают:  , а их элементы:
, а их элементы: 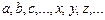 . Пустое множество обозначают
. Пустое множество обозначают 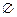 .
.
Множество  называют подмножеством множества
называют подмножеством множества 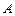 , если все элементы множества
, если все элементы множества  принадлежат множеству
принадлежат множеству 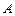 и пишут
и пишут  . Множества
. Множества 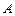 и
и  называют равными, если они состоят из одних и тех же элементов и пишут
называют равными, если они состоят из одних и тех же элементов и пишут 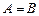 . Два множества
. Два множества 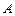 и
и  будут равны тогда и только тогда, когда
будут равны тогда и только тогда, когда  и
и  .
.
Множество 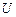 называют универсальным (в рамках данной математической теории), если его элементами являются все объекты, рассматриваемые в данной теории.
называют универсальным (в рамках данной математической теории), если его элементами являются все объекты, рассматриваемые в данной теории.
Множество можно задать: 1) перечислением всех его элементов, например:  (только для конечных множеств); 2) заданием правила
(только для конечных множеств); 2) заданием правила  определения принадлежности элемента
определения принадлежности элемента 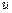 универсального множества
универсального множества 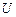 , данному множеству
, данному множеству 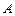 :
: 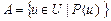 .
.
Объединением множеств 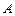 и
и  называется множество
называется множество
|
|
|
|
|
Дата добавления: 2014-12-08; Просмотров: 643; Нарушение авторских прав?; Мы поможем в написании вашей работы!