
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение. Полученное уравнение определяет гиперболу с центром в точке и осями симметрии параллельными координатным осям
|
|
|
|
.
.
.
.
Полученное уравнение определяет гиперболу с центром в точке 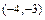 и осями симметрии параллельными координатным осям. Для построения гиперболы в системе координат
и осями симметрии параллельными координатным осям. Для построения гиперболы в системе координат 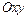 : 1) отмечаем центр гиперболы
: 1) отмечаем центр гиперболы 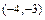 ; 2) проводим через центр
; 2) проводим через центр 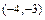 пунктиром оси симметрии гиперболы; 3) строим пунктиром основной прямоугольник гиперболы с центром
пунктиром оси симметрии гиперболы; 3) строим пунктиром основной прямоугольник гиперболы с центром 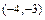 и сторонами
и сторонами 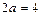 и
и 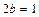 параллельными осям симметрии; 4) проводим через противоположные вершины основного прямоугольника пунктиром прямые, являющиеся асимптотами гиперболы, к которым неограниченно близко при бесконечном удалении от начала координат приближаются ветви гиперболы, не пересекая их; 5) изображаем сплошной линией ветви гиперболы (рис. 1).
параллельными осям симметрии; 4) проводим через противоположные вершины основного прямоугольника пунктиром прямые, являющиеся асимптотами гиперболы, к которым неограниченно близко при бесконечном удалении от начала координат приближаются ветви гиперболы, не пересекая их; 5) изображаем сплошной линией ветви гиперболы (рис. 1).
Ответ: Гипербола с центром в точке 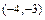 (см. рис.1)..
(см. рис.1)..

Рис.1
б) Выделяя полные квадраты в левой части
уравнения 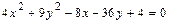 , преобразуем его следующим образом:
, преобразуем его следующим образом: 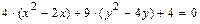
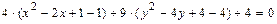
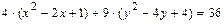
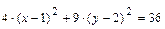
Полученное уравнение определяет эллипс с центром в точке 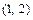 и осями симметрии параллельными осям координат. Для построения эллипса в системе координат
и осями симметрии параллельными осям координат. Для построения эллипса в системе координат 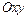 : 1) отмечаем центр эллипса
: 1) отмечаем центр эллипса 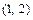 ; 2) проводим через центр
; 2) проводим через центр 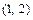 пунктиром оси симметрии эллипса; 3) строим пунктиром основной прямоугольник эллипса с центром
пунктиром оси симметрии эллипса; 3) строим пунктиром основной прямоугольник эллипса с центром 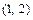 и сторонами
и сторонами 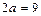 и
и 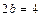 параллельными осям симметрии; 4) изображаем сплошной линией эллипс, вписывая его в основной прямоугольник так, чтобы эллипс касался его сторон в точках пересечения прямоугольника с осями симметрии (рис.2).
параллельными осям симметрии; 4) изображаем сплошной линией эллипс, вписывая его в основной прямоугольник так, чтобы эллипс касался его сторон в точках пересечения прямоугольника с осями симметрии (рис.2).
Ответ: Эллипс с центром в точке 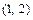 (см. рис.2).
(см. рис.2).
в). Выделяя полные квадраты в левой части уравнения  , преобразуем его следующим образом:
, преобразуем его следующим образом:
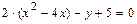
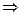
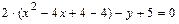
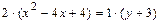
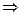
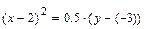
Полученное уравнение определяет параболу с вершиной в точке 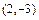 и осью симметрии параллельной оси
и осью симметрии параллельной оси 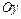 . Для построения параболы в системе координат
. Для построения параболы в системе координат 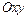 : 1) отмечаем вершину параболы
: 1) отмечаем вершину параболы 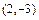 ; 2) проводим через вершину
; 2) проводим через вершину 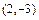 пунктиром ось симметрии параболы; 3) изображаем сплошной линией параболу, направляя её ветвь, с учётом того, что параметр параболы
пунктиром ось симметрии параболы; 3) изображаем сплошной линией параболу, направляя её ветвь, с учётом того, что параметр параболы 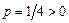 , в положительную сторону оси
, в положительную сторону оси 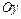 (рис.3).
(рис.3).
Ответ: Парабола с вершиной в точке 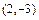 (см. рис.3).
(см. рис.3).
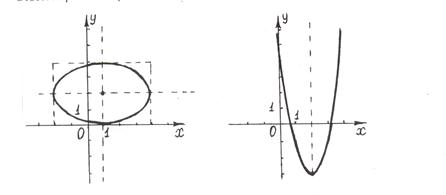
Рис.2. Рис.3.
9.1-30. Требуется:
а) найтиобласть определения функции  ;
;
б) установить чётность (нечётность) функции  .
.
Решение. а) Естественную область определения находим как множество 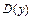 всех значений аргумента
всех значений аргумента 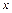 функции, для которых формула
функции, для которых формула  имеет смысл:
имеет смысл: 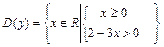 . Решив (на числовой прямой) систему неравенств
. Решив (на числовой прямой) систему неравенств 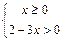 , устанавливаем, что геометрическим образом множества
, устанавливаем, что геометрическим образом множества 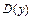 является промежуток
является промежуток 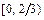 .
.
б) Находимсначала естественнуюобласть определения функции  :
: 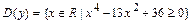 . Решив (на числовой прямой) неравенство
. Решив (на числовой прямой) неравенство 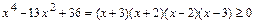 , устанавливаем, что геометрическим образом множества
, устанавливаем, что геометрическим образом множества 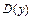 является объединение промежутков
является объединение промежутков 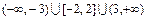 .
.
Так как область 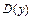 является симметричной относительно точки
является симметричной относительно точки 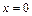 , то проверяем выполнение для всех
, то проверяем выполнение для всех 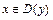 условий:
условий: 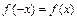 или
или 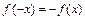 , учитывая чётность и нечётность основных элементарных функций, входящих в аналитическое выражение
, учитывая чётность и нечётность основных элементарных функций, входящих в аналитическое выражение 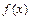 .
.
Если область 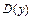 не симметрична относительно точки
не симметрична относительно точки 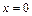 , то
, то 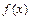 на этом множестве является функцией общего вида.
на этом множестве является функцией общего вида.
Для этого находим 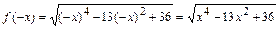 . Поскольку
. Поскольку 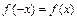 для всех
для всех 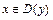
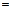
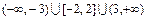 , то функция
, то функция  является чётной.
является чётной.
Ответ: а) 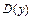
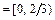 ,
,  ;
;
б) функция  - чётная.
- чётная.
10.1-30. Вычислить пределы (не пользуясь правилом Лопиталя):
а) 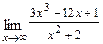 б)
б) 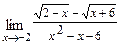 в)
в) 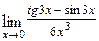 г)
г) 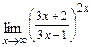 д)
д) 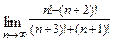
Вычисление предела 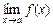 , где
, где 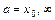 , начинают всегда с подстановки в
, начинают всегда с подстановки в 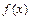 предельного значения её аргумента
предельного значения её аргумента 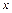 . В результате могут получиться неопределённости
. В результате могут получиться неопределённости 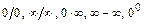 ,
, 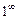 ,
, 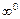 , которые раскрывают тождественными преобразованиями
, которые раскрывают тождественными преобразованиями 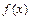 такими, чтобы преобразованное выражение получилось определённым. При вычислении пределов используют свойства конечных пределов и бесконечно больших функций, а также следующие известные пределы:
такими, чтобы преобразованное выражение получилось определённым. При вычислении пределов используют свойства конечных пределов и бесконечно больших функций, а также следующие известные пределы: 
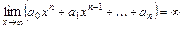 ,
, 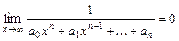 ,
, 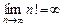 (
(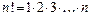 ),
), 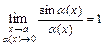 ,
, 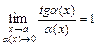 ,
, 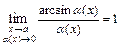 ,
, 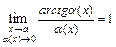 ,
, 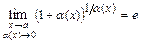 .
.
Решение. а) 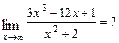 При подстановке вместо переменной
При подстановке вместо переменной 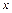 её предельного значения
её предельного значения 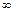 получим неопределённость
получим неопределённость 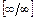 . Для её раскрытия сначала разделим числитель и знаменатель дроби на
. Для её раскрытия сначала разделим числитель и знаменатель дроби на 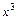 (старшую степень переменной
(старшую степень переменной 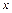 в числителе и знаменателе), после чего используем свойства конечных пределов и бесконечно больших функций. Получим
в числителе и знаменателе), после чего используем свойства конечных пределов и бесконечно больших функций. Получим 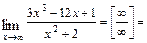
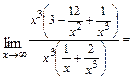
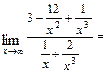
б) 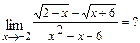 При подстановке вместо переменной
При подстановке вместо переменной 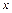 её предельного значения
её предельного значения 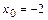 получим неопределённость
получим неопределённость 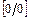 . Для её раскрытия выделим в числителе и знаменателе дроби общий множитель вида
. Для её раскрытия выделим в числителе и знаменателе дроби общий множитель вида 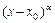 , где
, где 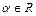 - некоторое число, т.е. множитель
- некоторое число, т.е. множитель 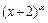 . Затем сократим на него числитель и знаменатель дроби, после чего используем свойства пределов.
. Затем сократим на него числитель и знаменатель дроби, после чего используем свойства пределов.
1) В квадратном трёхчлене 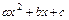 множитель выделяют разложением квадратного трёхчлена по формуле
множитель выделяют разложением квадратного трёхчлена по формуле 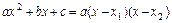 , где
, где 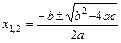 . 2) В выражении
. 2) В выражении 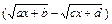 множитель выделяют следующим способом:
множитель выделяют следующим способом: 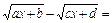
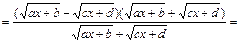
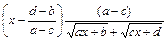 .
.
В результате получим 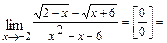
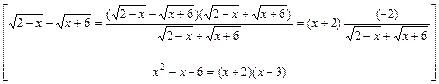
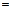
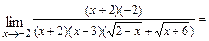
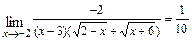 .
.
в) 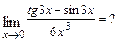 При подстановке вместо переменной
При подстановке вместо переменной 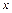 её предельного значения
её предельного значения 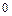 получим неопределённость
получим неопределённость 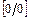 . Выделим в числителе множители вида
. Выделим в числителе множители вида 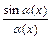 , где
, где 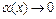 при
при 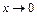 и используем свойства пределов. Получим
и используем свойства пределов. Получим
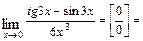
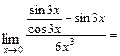
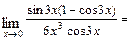
Для раскрытия неопределённостей 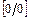 , содержащих тригонометрические и обратные тригонометрические функции, в числителе и знаменателе дроби выделяют сначала множители вида:
, содержащих тригонометрические и обратные тригонометрические функции, в числителе и знаменателе дроби выделяют сначала множители вида: 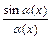 ,
, 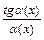 ,
, 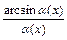 ,
, 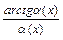 , где
, где 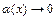 при
при 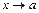 , используя формулы тригонометрии:
, используя формулы тригонометрии: 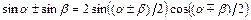 ,
, 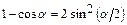 ,
, 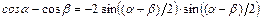 . После чего применяют свойства пределов, учитывая, что:
. После чего применяют свойства пределов, учитывая, что: 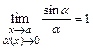 ,
, 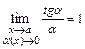 ,
, 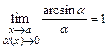 ,
, 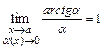 .
.
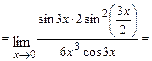

г) 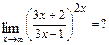
Для раскрытия неопределённости 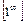 , возникающей при вычислении предела
, возникающей при вычислении предела 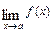 , где
, где 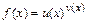 ,
, 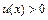 , сначала выражение
, сначала выражение 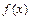 представляют в виде
представляют в виде 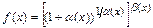 , где
, где 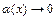 при
при 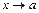 . После чего используют свойства пределов, заменяя выражение
. После чего используют свойства пределов, заменяя выражение 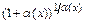 его предельным значением
его предельным значением  и учитывая, что
и учитывая, что 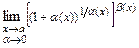 =
= 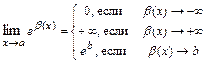 .
.
При подстановке вместо переменной 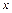 её предельного значения
её предельного значения 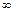 получим неопределённость
получим неопределённость 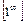 . Представим
. Представим 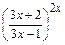 в виде
в виде 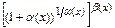 , где
, где 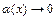 при
при 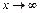 , следующим способом:
, следующим способом: 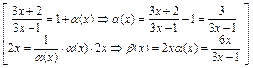
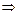
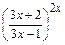 =
= 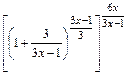 . Тогда учитывая, что
. Тогда учитывая, что 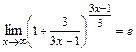 ,
, 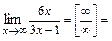
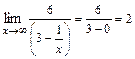 , получим
, получим  =
= 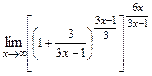
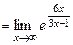 =
= 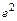 .
.
Ответ: а) 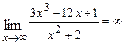 ; б)
; б) 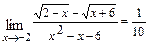 ; в)
; в) 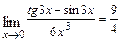 ; г)
; г) 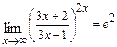 .
.
11.1-30. Для указанной функции 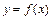 требуется: а) выяснить при каких значениях параметра
требуется: а) выяснить при каких значениях параметра 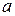 функциябудетнепрерывной; б) найтиточки разрыва функции и исследовать их характер. Построить график функции.
функциябудетнепрерывной; б) найтиточки разрыва функции и исследовать их характер. Построить график функции.
а) 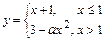 ; б)
; б) 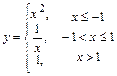 .
.
Точками разрыва функции 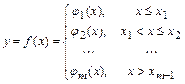 являются точки разрыва функций
являются точки разрыва функций 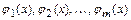 в промежутках
в промежутках 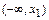 ,
, 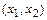 ,…,
,…, 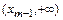 , кроме того, точками возможного разрыва функции
, кроме того, точками возможного разрыва функции 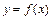 являются точки
являются точки 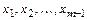 в окрестности которых и в самих точках функция задаётся разными аналитическими выражениями.
в окрестности которых и в самих точках функция задаётся разными аналитическими выражениями.
Точка  является точкой непрерывности функции
является точкой непрерывности функции 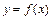 тогда и только тогда, когда:
тогда и только тогда, когда: 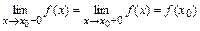 .
.
а) Поскольку функции 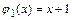 и
и 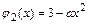 непрерывны в промежутках
непрерывны в промежутках 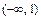 и
и 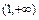 как элементарные функции, определённые в каждой точке данных промежутков, то непрерывностьфункции
как элементарные функции, определённые в каждой точке данных промежутков, то непрерывностьфункции 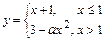 может нарушиться только в точке её возможного разрыва
может нарушиться только в точке её возможного разрыва 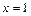 .
.
Определяем значение параметра 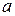 из условия непрерывности функции
из условия непрерывности функции 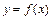 в точке
в точке 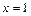 :
: 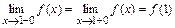 . Вычисляя
. Вычисляя 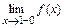 ,
, 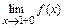 ,
, 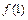 :
: 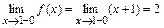 ,
, 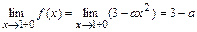 ,
, 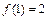 , из условия непрерывности
, из условия непрерывности 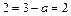 , находим
, находим 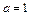 .
.
График непрерывной функции 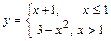 имеет вид изображённый на рис. 1.
имеет вид изображённый на рис. 1.
б) Функции 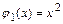 и
и 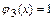 непрерывны в промежутках
непрерывны в промежутках 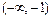 и
и 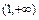 как элементарные функции, определённые в каждой точке данных промежутков, а функция
как элементарные функции, определённые в каждой точке данных промежутков, а функция 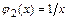 в промежутке
в промежутке 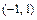 имеет точкой разрыва точку
имеет точкой разрыва точку 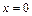 , в которой она не определена. Тогда для функции
, в которой она не определена. Тогда для функции 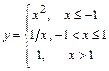 точка
точка 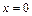 является точкой разрыва, а точки
является точкой разрыва, а точки 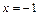 и
и 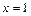 , в окрестности которых и в самих точках функция задаётся разными аналитическими выражениями, являются точками возможного разрыва.
, в окрестности которых и в самих точках функция задаётся разными аналитическими выражениями, являются точками возможного разрыва.
Исследуем на непрерывность точки 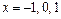 :
:
1) 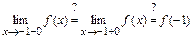
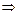
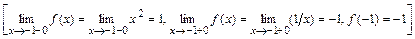
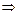
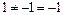 .
.
Следовательно, точка 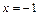 - точка разрыва 1-го рода функции
- точка разрыва 1-го рода функции 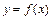 .
.
2) 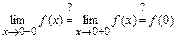
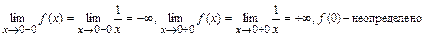 Следовательно, точка
Следовательно, точка 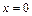 - точка бесконечного разрыва (2-го рода) функции
- точка бесконечного разрыва (2-го рода) функции 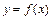 .
.
3) 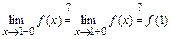
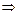
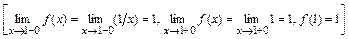
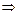
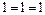 .
.
Следовательно, точка 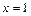 - точка непрерывности функции
- точка непрерывности функции 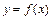 .
.
График функции 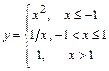 имеет вид, изображённый на рис.2.
имеет вид, изображённый на рис.2.
Ответ: а) Функция 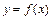 непрерывна при
непрерывна при 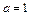 (рис.1); б)
(рис.1); б) 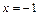 - точка разрыва 1-го рода,
- точка разрыва 1-го рода, 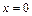 -точка бесконечного разрыва функции
-точка бесконечного разрыва функции 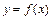 (рис.2).
(рис.2). 
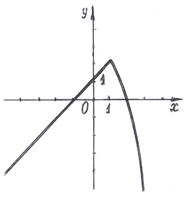
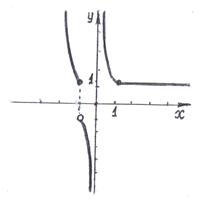
Рис.1 Рис.2
12.1-30. Даны комплексные числа 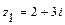 ,
, 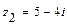 ,
,  и алгебраическое уравнение
и алгебраическое уравнение 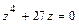 . Требуется: а) вычислить
. Требуется: а) вычислить 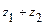 ,
, 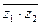 ,
, 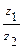 ; б) представить комплексное число
; б) представить комплексное число 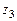 в тригонометрической форме, вычислить
в тригонометрической форме, вычислить 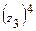 и результат представить в алгебраической форме; в) найти все корни алгебраического уравнения на множестве комплексных чисел.
и результат представить в алгебраической форме; в) найти все корни алгебраического уравнения на множестве комплексных чисел.
|
|
|
|
|
Дата добавления: 2014-12-08; Просмотров: 545; Нарушение авторских прав?; Мы поможем в написании вашей работы!