Математическая обработка результатов измерений

Ошибка результата определяется не только неточностями измерений, но и неточностями вычислений. Вычисления необходимо проводить так, чтобы их ошибка была на порядок меньше ошибки результата измерений. Для этого необходимо вспомнить правила математических действий с приближенными числами.

Значащими называются все цифры кроме нуля, стоящего слева от чисел. Нуль, стоящий между значащими цифрами или справа от них, также значащая цифра.

Примеры:

1) 0,0105. Два нуля слева – не значащие цифры. Всего число имеет три значащих цифры, в том числе и нуль, стоящий между значащими цифрами 1 и 5;

2) 5000. Нули справа – значащие. Всего число имеет четыре значащих цифры (нули получились не в результате округления, а при измерении);

3) 5∙10³. Число имеет одну значащую цифру, то есть при измерениях учитывались только тысячи. Точность числа 5∙10³ в тысячу раз меньше 5000.

Правила округления чисел

Если не все числа заканчиваются на одном и том же разряде, то для упрощения действий до их выполнения следует произвести округления до разряда на единицу меньшего, чем разряд наименее точного числа по правилам 1, 2 и 3.

Пример. .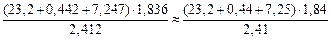

Правило 1. Округление достигается простым отбрасыванием цифр, если первая из отбрасываемых цифр меньше, чем 5.

Пример. 0,234 ≈ 0,23.

Правило 2. Если первая из отбрасываемых цифр больше, чем 5, то последняя цифра увеличивается на 1. Последняя цифра увеличивается также и в том случае, когда первая из отбрасываемых цифр 5, а за ней есть одна или несколько цифр, отличных от нуля.

Пример. 35,856 ≈ 35,9.

Правило 3. Если отбрасываемая цифра равна 5, а за ней нет значащих цифр, то округление производится на ближайшее четное число. Последняя сохраняемая цифра оставляется неизменной, если она четная, и увеличивается на единицу, если она нечетная.

Пример. 0,0465 ≈ 0,046; 0,935 ≈ 0,94.

При выполнении математических операций также возникает необходимость округления чисел, которое проводится в соответствии с правилами.

1. При сложении и вычитании приближенных чисел следует сохранить столько десятичных знаков, сколько их в приближенном данном с наименьшим числом десятичных знаков:

Пример. 23,2 + 0,442 + 7,247 ≈ 23,2 + 0,44 + 7,25 ≈ 30,9.

2. При умножении и делении приближенных чисел произведение или частное будет иметь столько значащих цифр, сколько их имеет приближенное данное с наименьшим числом значащих цифр:

Пример. ;

.

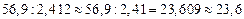3. При возведении в степень в результате сохраняется столько значащих цифр, сколько их имеет возводимое в степень приближенное число:

Пример. .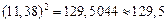

4. При извлечении корня сохраняется столько значащих цифр, сколько их имеет подкоренное выражение:

Пример. .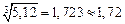

5. При нахождении логарифма из таблиц следует брать столько знаков, сколько значащих цифр содержит данное число:

Пример. .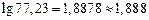

Число значащих цифр окончательного результата определяется порядком величины абсолютной погрешности. Таким образом, результат округляют до того разряда, в котором находится значащая цифра абсолютной ошибки.

Пример. , , .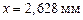

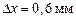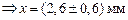Дата добавления: 2014-12-08