Основные определения. Внецентренное растяжение-сжатие – такой вид деформации, при котором стержень загружен растягивающими и (или) сжимающими силами

ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ-СЖАТИЕ СТЕРЖНЕЙ БОЛЬШОЙ ЖЕСТКОСТИ

Внецентренное растяжение-сжатие – такой вид деформации, при котором стержень загружен растягивающими и (или) сжимающими силами, приложенными вне центра тяжести поперечного сечения. При внецентренном растяжении-сжатии стержней (рис. 5.9) в стержне возникают три внутренних усилия: продольная сила (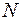) и два изгибающих момента ( 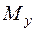и 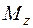). Предполагается, что стержень имеет большую жесткость, т. е. его длина не слишком велика по сравнению с размерами поперечного сечения. В этом случае определение усилий производим по недеформированному состоянию, т. е. при определении усилий не учитываем искривление оси стержня в результате изгиба. Используя правило знаков для изгибающих моментов, описанное во вступительной части разд. 5 "Сложное сопротивление", найдем внутренние усилия как сумму усилий от каждой силы. Тогда для стержня, показанного на рис. 5.9, согласно методу сечений получим

;

;

.

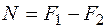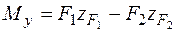Здесь 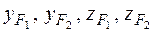– эксцентриситеты точек приложения сил, т. е. расстояния от сил до осе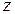й и 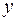(всегда положительны); и 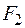– величины сил тоже считаются положительными. Знаки в формулах для 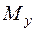и 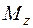соответствуют правилу знаков для изгибающих моментов. Поясним их. Относительно оси 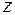сила вызывает изгиб стержня выпуклостью справа. Вся область сечения, расположенная справа от оси 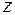, в том числе и первый (положительный) квадрант, окажется растянутой, поэтому эта сила создает положительный изгибающий момент. Сила 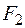вызывает изгиб стержня относительно оси 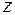тоже выпуклостью справа, поэтому знак изгибающего момента 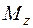от силы 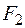опять положительный. При изгибе относительно оси 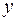передняя и задняя части сечения имеют напряжения разного знака. Сила вызывает изгиб стержня выпуклостью за осью 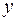, т. е. задняя часть сечения (а значит, и первый квадрант) окажется растянутой, поэтому 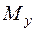от силы имеет знак плюс. 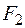Сила вызывает сжатие задней части сечения стержня, первый квадрант окажется сжатым, и знак изгибающего момента 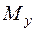от 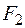отрицательный[7].

  Рис. 5.9. Внецентренное растяжение- сжатие жесткого стержня  

От найденных усилий в стержне возникают только нормальные напряжения, которые определяются по формуле (5.1). Для проверки прочности стержня необходимо найти максимальные напряжения. Определение этих напряжений производится по схеме, описанной ранее, т. е.:

· строим нейтральную линию по уравнению (5.2);

· находим положение опасных точек;

· подставляя в (5.1) координаты опасных точек, вычисляем напряжения в этих точках;

· для проверки прочности сравниваем максимальные напряжения с допускаемыми.

Если в сечении действует только одна сила, растягивающая или сжимающая, то формулу (5.1) можно преобразовать к такому виду:

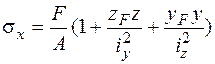, (5.9)

где

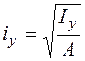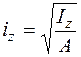, – (5.10)

радиусы инерции сечения относительно главных центральных осей; 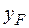, – координаты точки приложения силы; 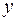, 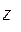– координаты точки, в которой определяются напряжения. Все координаты вычисляются в главной центральной системе осей инерции сечения. Уравнение нейтральной линии в этом случае будет иметь вид

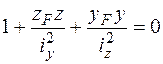. (5.11)

Используя уравнение нейтральной линии (5.11), найдем отрезки 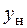, , 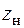отсекаемые нейтральной линией на осях координат (рис. 5.10),

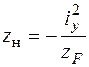; . (5.12)

Откладываем эти отрезки с учетом знаков вдоль главных центральных осей и строим нейтральную линию (см. рис. 5.10).

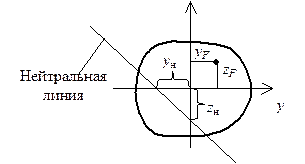Рис. 5.10. Положение нейтральной линии при внецентренном растяжении (сжатии) одной силой    

Из формул (5.12) следуют некоторые закономерности, связывающие положение полюса (т. е. точки приложения силы) и нейтральной линии, которые удобно использовать для анализа решения задачи. Перечислим самые важные из этих закономерностей:

1) нейтральная линия всегда расположена в квадранте, противоположном тому, в котором находится полюс (см. рис. 5.10);

2) если полюс находится на одной из главных осей, то нейтральная линия перпендикулярна этой оси;

3) если полюс приближается к центру тяжести сечения, то нейтральная линия удаляется от него;

4) если полюс движется по прямой линии, то нейтральная линия поворачивается вокруг неподвижной точки.

Рис. 5.11. Вид эпюры напряжений: а – для полюса, расположенного на контуре ядра сечения; б – для полюса, находящегося внутри ядра сечения

Из предпоследней закономерности следует, что если сила приложена достаточно близко к центру тяжести, то нейтральная линия удаляется так далеко, что нигде не пересекает сечение. Это означает, что напряжения во всем сечении будут иметь один знак. Следовательно, существует такая область вокруг центра тяжести, которая обладает следующим свойством: если внутри этой области или на ее контуре приложить силу (растягивающую или сжимающую), то во всем сечении будут возникать напряжения одного знака. Такая область называется ядром сечения. Рис. 5.11 поясняет данное определение ядра сечения. Нейтральная линия касается сечения, если сила приложена на контуре ядра сечения (см. рис. 5.11, а), и нейтральная линия проходит за сечением, если полюс расположен внутри ядра сечения (см. рис. 5.11, б).

Из приведенного определения ядра сечения следует первый способ построения ядра сечения. Согласно этому способу надо обвести контур сечения нейтральными линиями, касающимися контура и нигде не пересекающими сечение. Полюсы, соответствующие этим нейтральным линиям, будут находиться на контуре ядра сечения. На практике обычно более удобным является второй способ построения ядра сечения, который основан на свойстве взаимности нейтральной линии и полюса [2, гл. 7, § 36]. Для построения ядра сечения по второму способу надо поместить полюсы во внешних всех угловых точках сечения, имеющего форму многоугольника, и построить соответствующие им нейтральные линии. Эти нейтральные линии очертят контур ядра сечения. Отметим, что при построении ядра сечения нельзя располагать полюсы во внутренних угловых точках, так как через них нельзя провести касательные, нигде не пересекающие сечение. Рис. 5.12 поясняет разницу между внешними и внутренними угловыми точками многоугольника.

Для определения напряжений и проверки прочности стержня произвольного сечения, а также для построения ядра сечения необходимо научиться находить геометрические характеристики сечений, важнейшими из которых являются моменты инерции. Этому посвящен п. 5.2.1 гл. 5.

Рис. 5.12. Точки 1–5 –внешние, 6, 7 – внутренние угловые точки

5.2.1. Определение моментов инерции сложных сечений относительно главных центральных осей (задачи № 29, 30, 31)

Рекомендуемая литература

Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл. 4.

Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 15.

Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 5.

Дата добавления: 2014-12-08