
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Элементы векторной алгебры
|
|
|
|
Определение 1.4. Вектором называется направленный отрезок.
Вектор с началом в точке O и концом в точке M обозначим символом 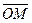 или
или 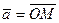 .
.
 A
A
O
Длину вектора 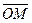 обозначим |
обозначим | 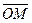 | или |
| или | 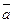 |. Вектор, у которого начало совпадает с концом, называется нулевым вектором.
|. Вектор, у которого начало совпадает с концом, называется нулевым вектором.
Определение 1.5. Векторы называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. Векторы, имеющие одинаковое направление, называются сонаправленными.
Определение 1.6. Два вектора считаются равными, если выполнены условия:
а) длины векторов равны;
б) векторы сонаправлены.
Следует различать начало и конец вектора. Поменяв их местами, мы получим уже другой вектор, направленный противоположно исходному.

 А А
А А
О О
Из определения равенства векторов следует, что при параллельном переносе вектора получаем вектор, равный исходному. Поэтому вектор можно переносить в любую точку плоскости или пространства.
Действия с векторами:
1. Сумма векторов.
Определение 1.7. Пусть даны два вектора 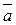 и
и  . Суммой векторов
. Суммой векторов 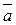 и
и  называют вектор
называют вектор 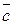 , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора 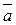 , а конец — с концом вектора
, а конец — с концом вектора  , при условии, что начало вектора
, при условии, что начало вектора  совпадает с концом вектора
совпадает с концом вектора 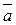 . Сумму векторов обозначают
. Сумму векторов обозначают  .
.
А



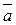
О В
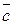
Правило сложения векторов, которое содержится в этом определении, называется правилом треугольника.
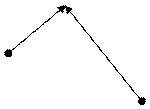
Это правило можно распространить на любое конечное число векторов. Для того чтобы построить сумму любого числа векторов, нужно в конце первого слагаемого вектора построить второй, в конце второго третий и т.д., сохраняя их длины и направление в пространстве или на плоскости. Вектор, замыкающий полученную ломаную линию, представляет собой искомую сумму. Начало его совпадает с началом первого вектора, конец — с концом последнего вектора (правило многоугольника).
Пусть, например, даны векторы 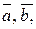
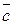 ,
, 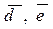 , расположенные указанным ниже образом. Тогда по правилу многоугольника имеем
, расположенные указанным ниже образом. Тогда по правилу многоугольника имеем
 А D
А D



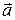
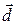
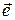
О 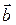

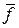 Е
Е

B 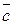 C
C
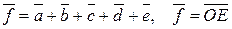
Правило сложения векторов может быть сформулировано ещё и следующим образом. Пусть имеем два вектора 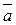 и
и  , выходящих из одной точки О. Отложим от точки А вектор
, выходящих из одной точки О. Отложим от точки А вектор 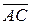 , равный вектору
, равный вектору  , а от точки В — вектор
, а от точки В — вектор 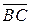 , равный вектору
, равный вектору 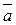 . Получим параллелограмм, построенный на векторах
. Получим параллелограмм, построенный на векторах 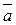 и
и  , как на сторонах. Очевидно, что суммой этих векторов будет вектор
, как на сторонах. Очевидно, что суммой этих векторов будет вектор 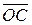 , который является диагональю этого параллелограмма. Такое правило сложения двух векторов называется правилом параллелограмма.
, который является диагональю этого параллелограмма. Такое правило сложения двух векторов называется правилом параллелограмма.



 A C
A C
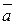
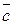
 O B
O B

Если два вектора 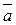 и
и  после приведения их к общему началу лежат на одной прямой и одинаково направлены, то их сумма
после приведения их к общему началу лежат на одной прямой и одинаково направлены, то их сумма 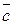 по определению есть вектор, длина которого равна сумме длин слагаемых векторов и направление совпадает с направлением этих векторов. Если слагаемые векторы направлены в противоположные стороны, то сумма их есть вектор
по определению есть вектор, длина которого равна сумме длин слагаемых векторов и направление совпадает с направлением этих векторов. Если слагаемые векторы направлены в противоположные стороны, то сумма их есть вектор 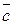 , длина которого равна разности длин слагаемых векторов, а направление совпадает с направлением вектора, имеющего большую длину.
, длина которого равна разности длин слагаемых векторов, а направление совпадает с направлением вектора, имеющего большую длину.
Операция сложения векторов имеет следующие свойства:
1) 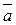 +
+  =
=  +
+ 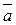 (коммутативность)
(коммутативность)
2) (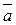 +
+  )+
)+ 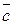 =
= 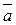 +(
+( +
+ 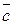 ) (ассоциативность)
) (ассоциативность)
2. Разность векторов.
Определение 1.8. Разностью двух векторов 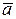 и
и 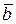 называется такой вектор
называется такой вектор 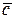 , который в сумме с вектором
, который в сумме с вектором 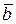 равен вектору
равен вектору 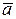 .
.
Обозначается таким образом: 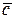 =
= 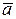 -
- 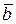 , если
, если 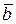 +
+ 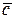 =
= 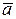 .
.
Вычитание векторов производится по следующему правилу: чтобы вычесть из одного вектора другой, нужно отнести их к общему началу и построить вектор из конца вычитаемого вектора в конец уменьшаемого вектора.
В
 |
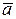
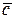
 А
А 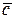 =
= 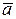 -
- 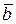 ,
, 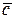 =
= 
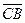

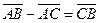
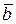
С
Определение 1.9. Два вектора 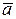 и
и  называются противоположными, если
называются противоположными, если 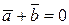 .
.
Из определения вытекает, что противоположные векторыимеют равные длины, но противоположные направления.


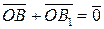
B O 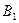
Вектор, противоположный вектору  , будем обозначать
, будем обозначать 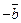 .
.
Тогда правило вычитания векторов можно сформулировать следующим образом: чтобы из вектора 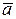 вычесть вектор
вычесть вектор  , нужно к
, нужно к 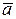 прибавить вектор
прибавить вектор 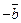 . Таким образом,
. Таким образом, 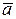 -
-  =
= 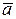 +(
+(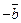 ).
).
3. Умножение вектора на число.
Определение 1.10. Произведением ненулевого вектора 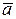 на вещественное число
на вещественное число 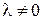 называется вектор, длина которого равна
называется вектор, длина которого равна 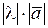 , направление совпадает с направлением вектора
, направление совпадает с направлением вектора 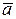 , если l>0 и меняется на противоположное, если l<0. Произведение любого вектора на число 0 есть
, если l>0 и меняется на противоположное, если l<0. Произведение любого вектора на число 0 есть 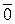 . Произведение нулевого вектора на любое число есть
. Произведение нулевого вектора на любое число есть 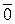 .
.
Умножение вектора на число обладает следующими свойствами:
1) l(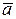 +
+  )=l
)=l 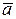 +l
+l  (дистрибутивность относительно сложения векторов).
(дистрибутивность относительно сложения векторов).
2) 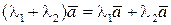 (дистрибутивность относительно сложения чисел).
(дистрибутивность относительно сложения чисел).
3) 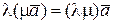 (ассоциативность).
(ассоциативность).
|
|
|
|
|
Дата добавления: 2014-12-08; Просмотров: 285; Нарушение авторских прав?; Мы поможем в написании вашей работы!