Простейшие задачи аналитической геометрии

Действия с векторами, заданными своими координатами

Рассмотрим действия с векторами, которые заданы своими координатами:

1) Равенство векторов. Два вектора 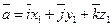и 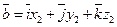равны тогда и только тогда, когда равны их соответствующие координаты: .

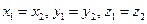2) При сложении векторов их одноименные координаты складываются, т.е.

,

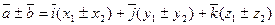или в координатной форме: .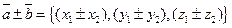

3) При умножении вектора 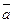на число l необходимо умножить на это число все его координаты:

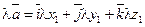, или .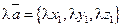

4) Рассмотрим скалярное произведение векторов, заданных своими координатами.

Пусть , найдём их скалярное произведение .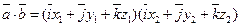

Согласно свойствам скалярного произведения, имеем

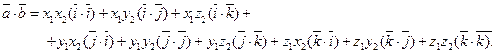
Так как 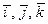— три взаимно перпендикулярных вектора, то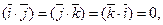 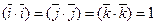и, следовательно,

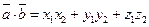, (1.3)

т.е. скалярное произведение равно сумме произведений одноименных координат.

1) Длина вектора. По свойству 4) скалярного произведения:

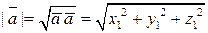. (1.4)

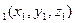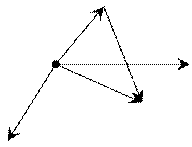
2) Расстояние между двумя точками в пространстве. Рассмотрим следующую задачу. Даны две точки M и M 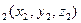(рис. 1.7). Найти расстояние между ними.

z

О y

x

Рис. 1.7

Заметим, что вектор 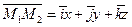есть разность векторов 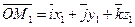и .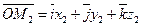

Таким образом, 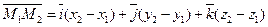. Следовательно, 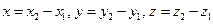. Применяя формулу (1.4), получим

.

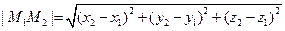Для плоскости эта формула имеет вид: .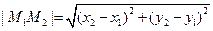

Пример 1.1. Определить расстояние между точкам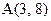и и .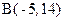

Решение. Воспользовавшись формулой (1.2), получим

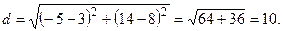
3) Угол между двумя векторами. Рассмотрим задачу об определении угла между двумя векторами. Согласно определению скалярного произведения векторов, имеем: ∙ = | |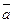| | 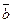cosj, где j — угол между векторам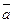и и 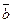. Из этой формулы находим

. (1.5)

Выражая числитель и знаменатель в координатной форме, получим формулу для вычисления угла между двумя данными векторами

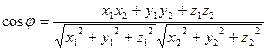. (1.6)

4) Направление вектора. Пусть a, b и g — углы, образованные вектором 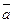с осями координат OX, OY и OZ соответственно. Имеем 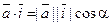. Отсюда

.

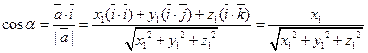Аналогично получим

; .

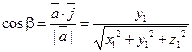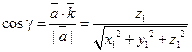Величины cosa, cosb, cosg называются направляющими косинусами вектора 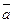. Имеет место очевидное равенство: .

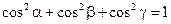5) Деление отрезка в заданном отношении. Пусть даны точки A (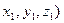 и B (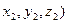. Будем говорить, что точка M (x,y,z) делит отрезок 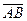в заданном отношении l, если .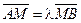

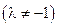B М

M В

A

А

O О

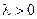
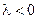
Требуется найти координаты точки M, делящей отрезок 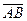в отношении l.

По условию имеем 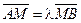. Замечая, что 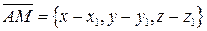, , 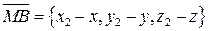, 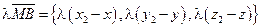перепишем это равенство в координатах: , , .

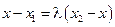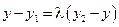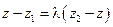Преобразовывая, получим координаты точки М:

.

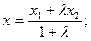
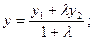
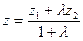Замечание 1. Если 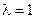, то М — середина отрезка АВ и тогда ее координаты:

.

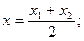
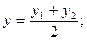
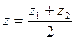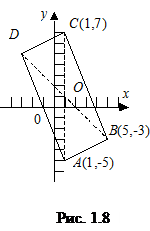Замечание 2. На плоскости координаты точки М, делящей отрезок 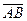в отношении l, имеют вид: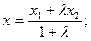 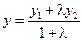, а координаты середины отрезка: .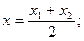

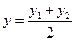Пример 1.2. Даны три вершины 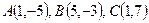параллелограмма . Найти его четвертую вершину D (рис. 1. 8).

Решение.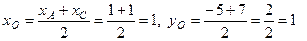

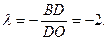
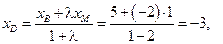
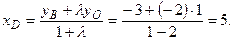
Ответ: D (-3:5).

Дата добавления: 2014-12-08