Выполнение работы. Проанализируйте поведение системы при различных параметрах ε, δ, х0

Проанализируйте поведение системы при различных параметрах ε, δ, х₀. Для этого:

1. Запишите закон изменения х(t) для заданных параметров.

2. Рассчитайте с помощью ПК или калькулятора х(t).

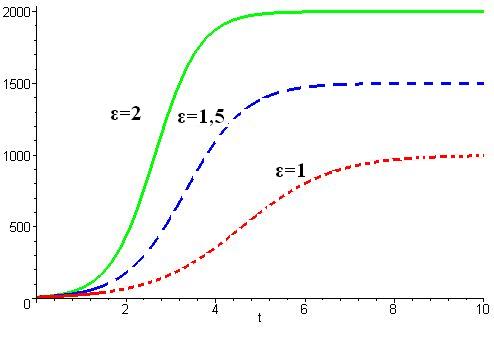А Б

В

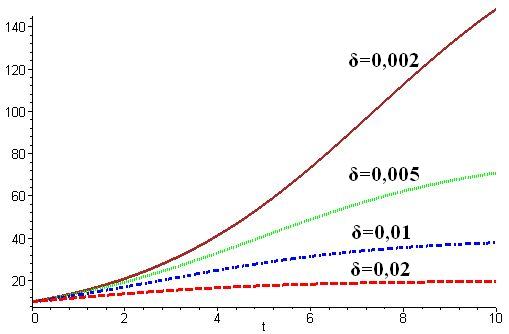
Рис. 2.2. Изменение численности особей при:

А) ε =const= 0,4, х₀=const=10;

Б) δ=const=0,001; х₀=const= 10; В) δ=const=0,01; ε =const=0,6.

3. Постройте графики х(t). Кривые для каждого вида параметров должны быть представлены на одном рисунке (см. примеры в теоретических сведениях).

4. Оцените характерные величины процесса:

а) Стационарное значение х_ст, сравните с расчетными данными

х_ст = ε /δ.

Постройте графики х_ст (ε), х_ст (δ).

б) Характерное время Т_0,9, когда численность популяции составляет х=0,9ст (т.е. практически выходит на стационарный уровень).

Постройте графики Т_0,9 (х₀), Т_0,9 (ε), Т_0,9(δ). Сделайте вывод.

в) параметры точки перегиба – время t_k и численность особей x_k, когда проявляется конкуренция их между собой (рис.2.3.).

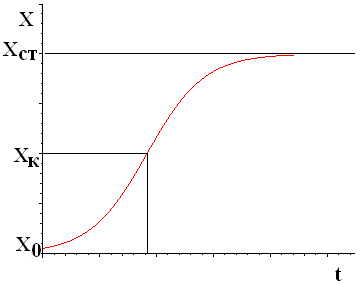
Рис.2.3. Положение точки перегиба.

Для этого по графику оцените x_k, сравните с теоретическим значением: .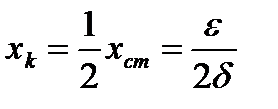

По графику найдите t_к.

Постройте графики х_к (ε), х_к (δ), х_к(х0), t_k(ε), t_k (δ), t_k(х0).

Сделайте вывод.

Задача № 1.Проанализируйте поведение системы при изменении коэффициента роста ε. Заполните таблицу:

Параметры	ε, 1/час.	δ, 1/час.	хо	Закон изменения х (t)	хст	хк	tк
1 система	2,2	0,001
2 система	1,6	0,001
3 система		0,001

Задача №2.Проанализируйте поведение системы при изменении коэффициента δ (вероятности конкуренции). Заполните таблицу:

Параметры	ε, 1/час.	δ, 1/час.	хо	Закон изменения х (t)	хст	хк	tк
1 система	0,4	0,001
2 система	0,4	0,003
3 система	0,4	0,01
4 система	0,4	0,02

Задача №3. Проанализируйте поведение системы при изменении начальной численности особей х₀. Заполните таблицу:

Параметры	ε, 1/час.	δ, 1/час.	хо	Закон изменения х (t)	хст	хк	tк
1 система	0,6	0,001
2 система	0,6	0,001
3 система	0,6	0,001
4 система	0,6	0,001

Задание 3. Циклические математические модели: модель "хищник-жертва" (модель Вольтера-Лотки)

Среди допущений, введенных в модели 1, снимем допущение 4. Пусть в некотором пространстве живут два вида особей: зайцы (жертвы) и рыси (хищники). Зайцы питаются растительной пищей, имеющейся всегда в достаточном количестве (между ними отсутствует внутривидовая борьба). Рыси могут питаться только зайцами.

Введем величины:

х - число жертв в момент t;

у - число хищников в момент t;

Уравнения баланса между численностью рожденных и гибнущих особей:

Жертвы: 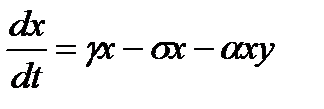; хищники:

γx, δxy - скорость размножения

σx, βy - скорость естественной гибели

αxy - скорость гибели за счет встречи с хищником

или 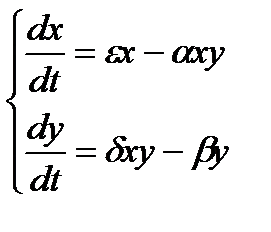(1)

Это сложная система нелинейных дифференциальных уравнений. Сначала найдем стационарное решение х = const, у =const, то есть dx/dt=0, dy/dt=0. Система дифференциальных уравнений при этом сводится к алгебраическим:

X_СТ(ε-αy_СТ)=0; Y_СТ(δx_СТ -β) (2)

Рассмотрим решения:

X_СТ= β/δ; Y_СТ= ε/α (3)

Упростим систему уравнений (1), предполагая, что произошли малые отклонения численности хищников V(t) и жертв U(t) относительно стационарных значений:

x=x_СТ+U(t), U<x_СТ,U<y_СТ (4)

y=y_СТ+V(t), V<y_СТ,V<x_СТ (5)

Тогда

dU/dt=x_СТ(ε-αy_СТ)+U(ε-αy_СТ)-αx_СТV- αUV,

dV/dt=y_СТ(δx_СТ -β)+V(δx_СТ-β)- δy_СТU- δUV,

или

,

.

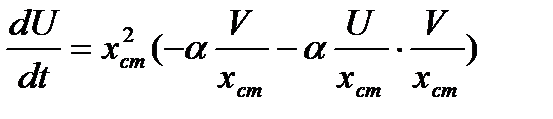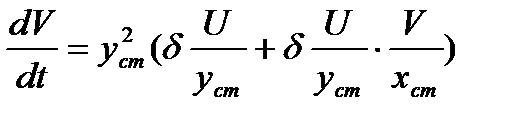Учитывая (1) и пренебрегая членами второго порядка малости 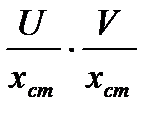и , получим систему уравнений:

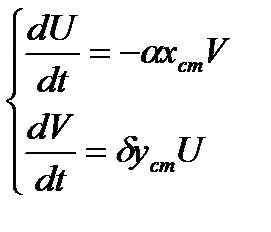(6)

которую легко свести к дифференциальным уравнениям второго порядка относительно переменных U и V:

,

.

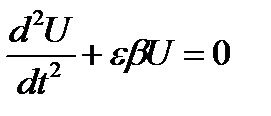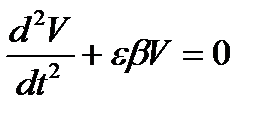Это характерные уравнения для описания гармонических колебательных процессов. Решения уравнений:

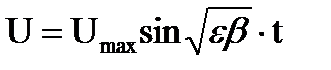, (7)

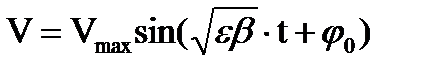, (8)

Отношение амплитуд отклонений: .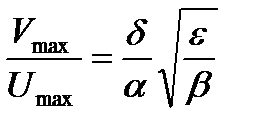

В результате численности особей при малых отклонениях от стационарных значений равны:

,

.

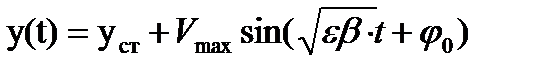Таким образом, численности популяций х и y испытывают гармонические колебания относительно стационарных значений с одинаковой частотой 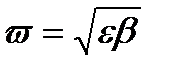, но смещение по фазе на . Периодичность изменения численности хищников и жертв наблюдалась и на опыте. На рис.2.4. приведены опытные данные по количеству числа добытых шкурок зайцев и рысей в Канаде с 1845 по 1935 годы.

Видно, что в реальном случае зависимости более сложные, чем это следует из модели. Необходимо подчеркнуть, что синусоидальное решение возможно лишь при малых отклонениях U и V относительно стационарных значений. При больших отклонениях закон не будет гармоническим (рис.2.4). Тем не менее, данная модель вполне адекватна действительности: колебания численностей хищников и жертв происходят с одинаковой частотой, наблюдается смещение колебаний по фазе.

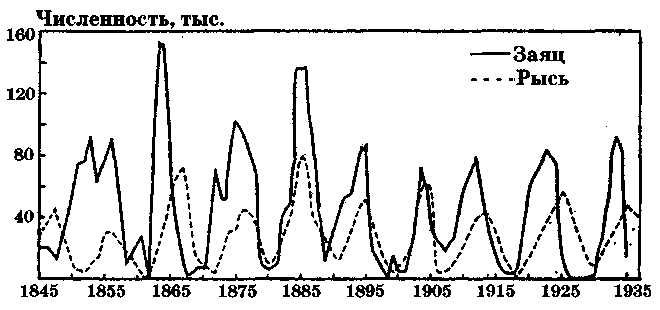
Рис.2.4. Динамика популяции зайцев и рысей.

Зависимость y от x можно представить и виде фазового портрета. Для периодических зависимостей портрет имеет вид эллипса (рис.2.5), цент которого соответствует стационарным значениям.

Рис. 2.5. Фазовый портрет системы при малых отклонениях численности хищников и жертв от стационарных значений

Допустим, произошло отклонение численности зайцев от ста-ционарного значения (1→2). Если число зайцев возросло, то число рысей также увеличивается, но количество зайцев при этом постепенно начнет уменьшаться (точка 3). Это повлечет уменьшение числа рысей (точка 4), а "следовательно увеличение числа зайцев (точка 1).

Модель «хищник-жертва» используется в настоящее время в медицине. Так при моделировании онкологических заболеваний опухолевые клетки рассматриваются как жертвы, а лимфоциты, которые могут их подавлять, как хищники. В этом случае моделирование позволяет получить новые знания о процессах межклеточного взаимодействия при этих патологиях, находить пути оптимальной стратегии лечения, создавать новые средства борьбы с ними.

Дата добавления: 2014-11-29