Практическая часть. 1. Научиться составлять и решать (аналитически и с помощью ПК) кинетические уравнения при моделировании процессов изменения численности популяций

Цель работы:

1. Научиться составлять и решать (аналитически и с помощью ПК) кинетические уравнения при моделировании процессов изменения численности популяций.

2. Проводить анализ полученных решений, графически представлять результаты.

Задание 1. Модель естественного роста (модель Мальтуса)

Реальная система: имеется некоторая популяция одного вида (микроорганизмы, зайцы и т.п.), в которой происходят жизненные процессы во всем их многообразии.

Постановка задачи. Найти законы изменения численности популяции во времени.

Основные допущения:

1. Существуют только процессы размножения и естественной гибели, скорости которых пропорциональны численности особей в данный момент времени.

2. Не учитываем биохимические, физиологические процессы.

3. Нет борьбы между особями за место обитания, за пищу (бесконечно большое пространство и количество пищи).

4. Рассматриваем только одну популяцию, нет хищников.

Модель.

Введем величины:

х — численность популяции в момент t;

R — скорость размножения, γ— коэффициент размножения;

S— скорость естественной гибели, σ — коэффициент естественной гибели;

- скорость изменения численности популяции, ε-коэффициент роста.

Тогда R =γx, S =- σх.

Составим дифференциальное уравнение баланса: изменение численности особей в единицу времени определяется количеством рожденных за это время и умерших:

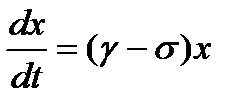, или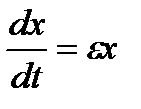

Начальное условие: при t=0 численность особей х = х₀, Решим уравнение:

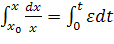à 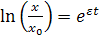, отсюда

Графики для различных параметров системы приведены на рис. 2.1.

А Б

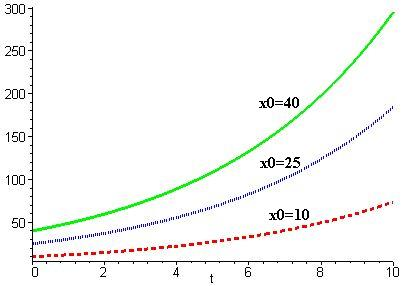В Г

Рис. 2.1. Изменение численности особей при: А) ε>0, γ>σ, x0=10; Б) ε< 0, γ<σ, x₀=100; В) ε= 0, γ=σ; Г) ε=const=0,2.

Дата добавления: 2014-11-29