Силы в природе

Из кинематики известно, что знание величины и направления ускорения позволяет вычислить значения радиуса - вектора материальной точки в любой последующий момент времени, т.е. предсказать положение точки. Законы динамики позволяют сделать это, если известна правая часть уравнений (2-3). Другими словами, нужно уметь определять силы, действующие на тело, положение которого требуется описать. Взаимодействие между макроскопическими телами физика сводит к взаимодействию между элементарными частицами. Таких элементарных частиц в настоящее время известно более сотни. Среди них наиболее популярны электрон, протон и нейтрон. Для характеристики всех частиц вводятся такие понятия как масса покоя, электрический заряд, собственный механический момент (спин), а также четность, странность, красивость, барионный заряд, цветовой заряд, слабый заряд и т.д. Установлено, что между элементарными частицами существует четыре фундаментальных взаимодействия: сильное, слабое, электромагнитное и гравитационное. Сравнительные характеристики этих взаимодействий приведены в таблице 2.1.

Таблица 2.1.

Название вза-имодействия	Относительная интенсивность	Частица,«пере-носящая» взаи-модействие	Характеристи-ка частицы
Сильное	1	p-мезоны (глюоны)(8 типов)	m ~250 mэлект разнообразные
Электромаг- нитное	10^-2	фотон	E= hn
Слабое	10^-13	W - частицы Z - частицы	Е ~10^2 с^2 m протон гипотетичны
Гравитацион- ное	10^-40	гравитон	гипотетичен

Из таблицы 2.1 видно, что гравитационные силы являются слабейшими из всех фундаментальных взаимодействий, однако они обладают свойствами аддитивности и достигают значительных величин в космическом масштабе (притяжение Луны, строение Солнечной системы и т.п.). Величина гравитационной силы притяжения двух точечных масс m₁ и m₂ определена Ньютоном и известна как закон всемирного тяготения:

, (2-6)

где r - расстояние между массами, а G = 6,67 10 ^-11 Н· м²/кг² - гравитационная постоянная. Чтобы подчеркнуть, что сила - вектор, закон записывают несколько иначе, рассматривая силу, действующую на m₂ со стороны m₁:

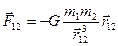, (2-7)

откуда видно направление силы (она направлена вдоль прямой, соединяющей взаимодействующие массы). Модуль силы притяжения P тела массы m к Земле, которую называют силой тяжести можно записать так:

(2-8)

где величина - ускорение свободного падения, М_З- масса Земли, а R_З - радиус Земли. Из выражения g видно, что оно не зависит от массы выбранного тела и поэтому одинаково для всех тел в определенной точке земной поверхности.

Кроме гравитационных сил в механике рассматриваются упругие силы и силы трения, которые обусловле ны электрическими силами. Силы упругости обусловлены деформациями. Деформации связаны с изменением взаимного расположения молекул, образующих рассматриваемое тело, причем силы возникают лишь тогда, когда деформации носят упругий характер. В этом случае справедлив закон Гука так, что

,

где x обозначает величину упругой деформации, а к - коэффициент пропорциональности, зависимый от свойств деформируемого тела и вида деформации. Частным примером проявления упругих сил служат силы реакции опор, направление которых считается всегда нормальным (перпендикулярным) к деформируемой поверхности. Другим примером действия упругих сил могут служить так называемые силы связи (силы натяжения).

Силы трения препятствует скольжению соприкасаю­щихся тел друг относительно друга. Силы трения зависят от относительных скоро­стей тел. Силы трения могут быть разной природы, но в результате их действия ме­ханическая энергия всегда превращается во внутреннюю энергию соприкасающих­ся тел.

Различают внешнее (сухое) и внутрен­нее (жидкое или вязкое) трение. Внешним трением называется трение, возникающее в плоскости касания двух соприкасающих­ся тел при их относительном перемещении. Если соприкасающиеся тела неподвижны друг относительно друга, говорят о трении покоя, если же происходит относительное перемещение этих тел, то в зависимости от характера их относительного движения говорят о трении скольжения, качения или верчения.

Внутренним трением называется тре­ние между частями одного и того же тела, например между различными слоями жид­кости или газа, скорости которых меняют­ся от слоя к слою. В отличие от внешнего трения здесь отсутствует трение покоя. Если тела скользят относительно друг дру­га и разделены прослойкой вязкой жидко­сти (смазки), то трение происходит в слое смазки. В таком случае говорят о гидроди­намическом трении (слой смазки доста­точно толстый) и граничном трении (тол­щина смазочной прослойки ~0,1 мкм и меньше).

Обсудим некоторые закономерности внешнего трения. Это трение обусловлено шероховатостью соприкасающихся повер­хностей; в случае же очень гладких по­верхностей трение обусловлено силами межмолекулярного притяжения.

Рассмотрим лежащее на плоскости те­ло (рис.2.1), к которому приложена горизонтальная сила F.

Рис.2.2

Тело придет в движе­ние лишь тогда, когда приложенная сила 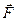будет больше силы трения 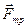. Француз­ские физики Г. Амонтон (1663—1705) и Щ. Кулон (1736—1806) опытным путем установили следующий закон: сила трения скольжения F_тр пропорциональна силе N нормального давления, с которой одно тело действует на другое:

F_тр =fN,

где f — коэффициент трения скольжения, зависящий от свойств соприкасающихся поверхностей.

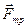Найдем значение коэффициента тре­ния. Если тело находится на наклонной плоскости с углом наклона (рис.2.2), то оно приходит в движение только когда тангенциальная составляющая F силы тя­жести больше силы трения . Следова­тельно, в предельном случае (начало скольжения тела) F=F _тр

или откуда .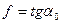

Таким образом, коэффициент трения ра­вен тангенсу угла a₀, при котором на­чинается скольжение тела по наклонной плоскости.

Для гладких поверхностей определен­ную роль начинает играть межмолекуляр­ное притяжение. Поэтому Б. В. Дерягиным (р. 1902) предложен закон трения скольжения

,

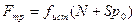где p₀ — добавочное давление, обус­ловленное силами межмолекулярного при­тяжения, которые быстро уменьшаются с увеличением расстояния между частица­ми; S — площадь контакта между телами; — истинный коэффициент трения скольжения.

Трение играет большую роль в при­роде и технике. Благодаря трению движет­ся транспорт, удерживается забитый в стену гвоздь и т. д.

В некоторых случаях силы трения ока­зывают вредное действие, и поэтому их надо уменьшать. Для этого на трущиеся поверхности наносят смазку (сила трения уменьшается примерно в 10 раз), которая заполняет неровности между этими повер­хностями и располагается тонким слоем между ними так, что поверхности как бы перестают касаться друг друга, а скользят друг относительно друга отдельные слои жидкости. Таким образом, внешнее трение твердых тел заменяется значительно мень­шим внутренним трением жидкости.

Радикальным способом уменьшения силы трения является замена трения скольжения трением качения (шариковые и роликовые подшипники и т.д.). Сила трения качения определяется по закону Кулона:

F _тр = f _kN/r,

где r — радиус катящегося тела; f_k — коэффициент трения качения.

Дата добавления: 2014-12-10