Нагрузкой

Пусть нагрузка равномерно распределяется на части линии. На рис. 4. 7 показаны такая линия, график распределения тока I _н и потери напряжения ∆ U вдоль линии.

Потеря напряжения в линии складывается из двух составляющих

∆ U_{a 2} = ∆ U_{a 1} + ∆ U ₁₂

Очевидно, при постоянном сечении линии S = const потеря напряжения на участке a1 равна

∆ U_{a 1} = I _H r_{a 1} = I _H L ₁/γ S.

Потеря напряжения ца участке 1 – 2 с распределенной нагрузкой находится так:

.

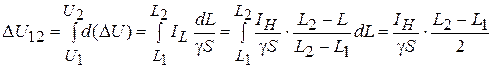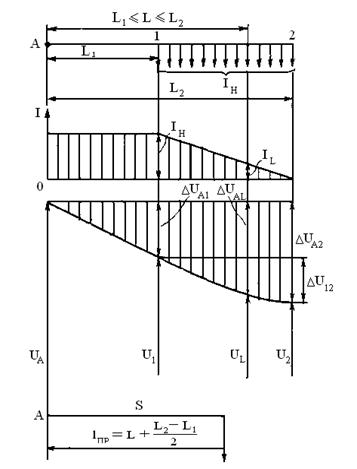
Рис. 4.7. Простая разомкнутая сеть с равномерно распределенной нагрузкой.

I_н- суммарный ток нагрузки; I_L- ток в сечении L; ∆U_А2- потеря напряжения в сети; ∆U_А1, ∆U_АL, ∆U₁₂- потеря напряжения на соответствующих участках сети.

Из уравнений находим сечение провода

S = I _H l _пр/γ∆ U _доп.

Приведенная длина линии l _пр при равномерной нагрузке:

l _пр= L _{1 +} (L ₂ - L ₁)/2.

Таким образом, линия с равномерно распределенной суммарной нагрузкой I _H эквивалентна линии с сосредоточенной нагрузкой I _H, приложенной к середине загруженного участка линии. Если нагрузка равномерно распределена вдоль всей линии (l₁ = o), то приведенная длина определяется как l _пр=0,5 L ₂; если при этом налицо некоторая не­равномерность распределения нагрузки, то l _пр = (0,4 ÷ 0,6) L ₂, причем 0,4 соответствует большей нагрузке в конце линии, а 0,6 – в начале линии.

3. Разомкнутая сеть с несколькими сосредоточенными нагрузками (рис. 4.8).

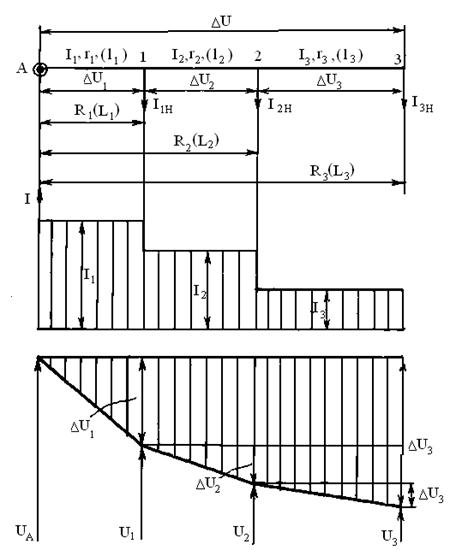
Рис. 4.8. Разомкнутая цепь с несколькими сосредоточенными нагрузками:

∆ U - потеря напряжения в сети; ∆ U ₁, ∆ U ₂… ∆ U _k- потеря напряжения на участках; I ₁, I ₂… I _k- токи на участках; r ₁(l ₁), r ₂(l₂)… r_k (l_k)- сопротивления(длины) участков; R ₁(L ₁), R ₂(L ₂)… R_k (L_k)- сопротивления(длины) частей линии от источника А до приложения соответствующего тока нагрузки; I _1н, I _2н… I_{k н}- токи нагрузок

,

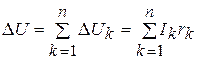где I_k – сила токов,

R_k – сопротивление,

L_k – длина,

Δ U_k – падение напряжения,

I_kn – токи нагрузки потребителей,

R_ka – сопротивления участков сети,

L_ka – длины от питательного пункта А до точки приложения k - ой нагрузки.Потери напряжения в сети

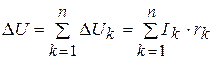(4. 12)

при n сосредоточенных нагрузках

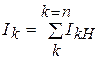
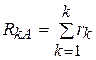от А до К нагрузки (4. 13)

Из (4. 12) и (4. 13) уравнение потери напряжения в сети с n неизвестными сечениями участков Sк

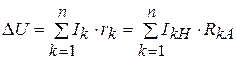(4. 14)

Дополнительные условия S_k = const, j_k = const, вес сети V = V _min

Первый вид расчета: S = Sk = const

Выражение (4. 14) можно записать в двух видах:

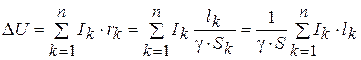(4. 15)

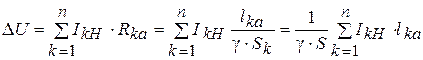(4. 16)

Введем понятие – суммарный момент токов относительно пункта А из (4. 15) и (4. 16)

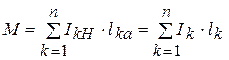(4. 17)

Искомое сечение сети S = M /γ U _доп

Удельное сопротивление меди при температуре Т о = 15 ^оС –

0.0175, Ом мм² /м; при температуре Т –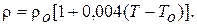

Второй вид расчета: 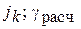– const.

Запишем (4. 14) в виде:

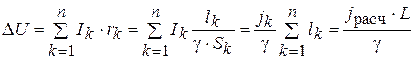. (4. 18)

Из (4.18) j _расч = γΔ U _доп/ L,

где L – длина линии с допустимой потерей напряжения

Δ U _доп.– допустимые потери напряжения в линии.

Тогда S_k = I_k / j _расч .

Третий вид расчета: расчет на минимум веса сети. V = V _min

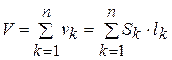(4. 19)

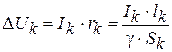(4. 20)

S_k = I_kl_k /γ Δ U_k

из (4. 19) и (4. 20) имеем

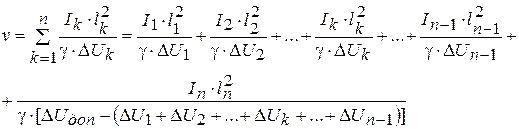(4. 21)

Найдем минимум функции U = U (Δ U ₁ Δ U _2... Δ U_{k ……} Δ U_{n -1}).

Из уравнения (4. 21) получим

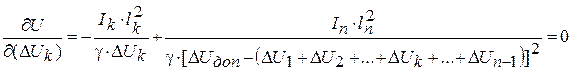. (4. 22)

Из (4. 22) с учетом (4. 21) 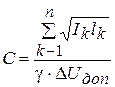(4. 23)

и 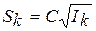(4. 24)

Пример: Дана сеть с несколькими сосредоточенными нагрузками (рис. 4. 9). Рассчитать тремя методами объем проводов.

На 4. 9 введены обозначения: v _S – объем меди сети при расчете на постоянство сечения; v_j – объем меди при расчете на постоянство плотности тока; v _min – минимум меди сети при заданной потере напряжения; S ₁, S ₂-– сечения участков сети.

1) S ₁ = S ₂ = S S ₁/ S ₂ = 1

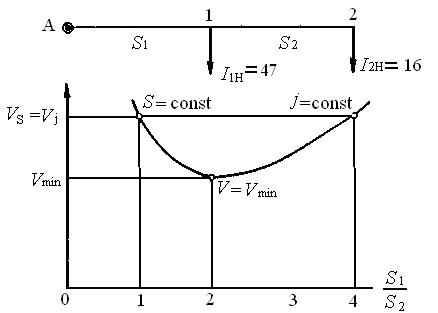
Рис. 4.9. График сравнения трех видов расчета сети с несколькими сосредоточенными нагрузками

2) 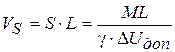(4. 25)

3)

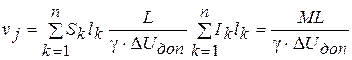
При любом способе расчета данной сети наиболее нагруженным в тепловом отношении является головной участок, который в первую очередь проверяется по допустимому нагреву. Нетрудно показать, что наиболее рациональное распределение меди между участками с точки зрения нагрева получается при расчете на постоянство плотности тока.

В общем случае расчет разомкнутой сети с несколькими сосредоточен­ными нагрузками надо вести всеми тремя способами, выбирая каждый раз ближайшие стандартные сечения участков (для головного участка и рядом лежащих – ближайшие большие, для концевых – ближайшие меньшие).

После этого надо проверить реальную потерю напряжения и нагрева, затем путем сравнения трех фактических вариантов расчета выбрать оптимальный.

Дата добавления: 2014-12-10