
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Векторов к доказательству теорем
|
|
|
|
Скалярного умножения векторов
А10. 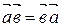
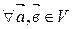 .
.
А20. 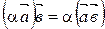 ;
; 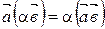
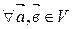
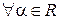 .
.
А30. 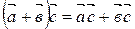
 .
.
Следствие.  . Это свойство можно распространить и на большее число слагаемых.
. Это свойство можно распространить и на большее число слагаемых.
Теорема 1 (скалярное произведение в координатах). Если в ортонормированном базисе 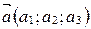 ,
, 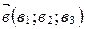 , то
, то
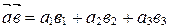 .
.
□ По определению координат вектора 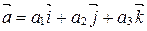 ,
,  . Используя свойства Г10,Г20, А10-А30 и то, что
. Используя свойства Г10,Г20, А10-А30 и то, что  ,
,  ,
, 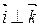 и
и  , получаем:
, получаем:
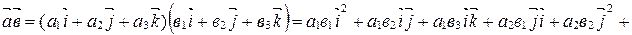
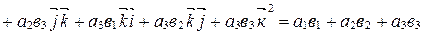 . ■
. ■
Следствие 1.  .
.
Следствие 2 (условие ортогональности двух векторов в координатах).
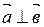
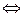
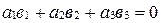 .
.
Следствие 3. 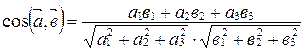 .
.
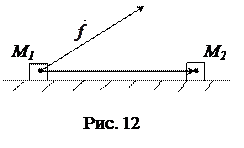 В физике скалярное произведение векторов применяется для вычисления работы силы
В физике скалярное произведение векторов применяется для вычисления работы силы  по перемещению материальной точки из положения
по перемещению материальной точки из положения 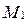 в положение
в положение 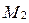 (рис. 12):
(рис. 12):
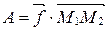 .
.
Скалярное умножение векторов широко применяется к решению содержательных геометрических задач и доказательству теорем.
Приведем пример доказательства теоремы Пифагора и теоремы косинусов.
Приложение скалярного произведения
1. Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
□ Пусть в 
 . Докажем, что
. Докажем, что 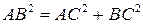 .
.
 Запишем сначала векторное равенство для векторов, содержащих стороны
Запишем сначала векторное равенство для векторов, содержащих стороны 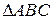 , применив правило треугольника:
, применив правило треугольника:
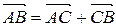 (рис. 13).
(рис. 13).
Возведем это векторное равенство в скалярный квадрат: 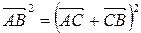 .
.
По следствию из свойства А30
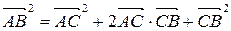
 .
.
Так как  , то по свойству Г10
, то по свойству Г10 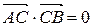 . Применив Г20, получаем:
. Применив Г20, получаем:
 .
.
Учитывая, что 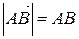 ,
, 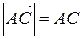 ,
, 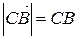 (т.е. длина вектора
(т.е. длина вектора 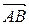 - это длина отрезка АВ), окончательно будем иметь:
- это длина отрезка АВ), окончательно будем иметь:
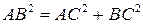 . ■
. ■
2. Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.
 □ Докажем, что
□ Докажем, что 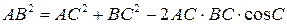 (рис. 14).
(рис. 14).
Представим вектор 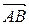 в виде разности векторов двух других сторон:
в виде разности векторов двух других сторон:
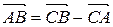 .
.
Возведем обе части этого векторного равенства в скалярный квадрат:
 .
.
Далее воспользуемся следствием из свойства А30:
 .
.
Учитывая, что  ,
, 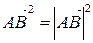 ,
, 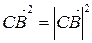 и
и 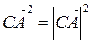 , получим:
, получим:
 ,
,
откуда
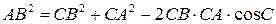 . ■
. ■
Задания для самостоятельной работы
 1. Найдите величину угла между векторами
1. Найдите величину угла между векторами 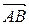 и
и 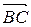 (рис. 15).
(рис. 15).
2. Может ли величина угла между векторами равняться 2700?
3. Произведение 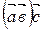 - это число или вектор?
- это число или вектор?
4. Верно ли равенство 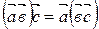 ? Если да, то докажите его справедливость для любых векторов
? Если да, то докажите его справедливость для любых векторов  ,
, 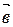 и
и 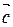 ; если нет, то приведите пример, подтверждающий этот вывод.
; если нет, то приведите пример, подтверждающий этот вывод.
5. Докажите, пользуясь скалярным произведением, что диагонали ромба взаимно перпендикулярны, а диагонали квадрата не только взаимно перпендикулярны, но и равны.
|
|
|
|
|
Дата добавления: 2014-12-10; Просмотров: 3027; Нарушение авторских прав?; Мы поможем в написании вашей работы!