Множественная корреляция

В приведенных выше примерах рассматривалась зависимость между двумя показателями. На практике же чаще всего изменение изучаемого показателя зависит от действия нескольких факторов. В таких случаях изучение корреляционной связи не может ограничиваться парными зависимостями, и в анализ необходимо включить другие факторы, существенно влияющие на изучаемую зависимую переменную. Одновременное изучение корреляции нескольких переменных проводится на основе использования методов множественной корреляции. Так, рассматривая уровень фондоотдачи на различных предприятиях одной отрасли, мы можем установить, что ее величина зависит от размеров предприятия, удельного веса активной части фондов, степени изношенности фондов, их обновления и ряда других факторов.

Если обозначить факторы 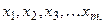то линейное уравнение множественной зависимости может быть записано так:

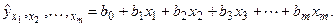
Рассчитав параметры уравнения множественной зависимости, определяем значение индекса корреляции по следующей формуле:

, (5.9)

где 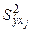— дисперсия эмпирических значений относительно значений, рассчитанных по уравнению регрессии, которая определяется делением остаточной суммы квадратов отклонений результативного показателя на (n-m-1);

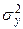— дисперсия эмпирических значений результативного показателя.

По параметрам полученного уравнения можем оценить долю каждого из факторов в изменении уровня результативного показателя у. Это может быть сделано путем прямой оценки по величине коэффициентов регрессии при каждом из факторов, а также по коэффициентам эластичности Э 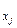, cтандартизированным частным коэффициентам регрессии 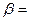коэффициентам и 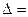коэффициентам.

Коэффициенты уравнения множественной регрессии показывают абсолютный размер влияния факторов на уровень результативного показателя и характеризуют степень влияния каждого фактора на анализируемый показатель при фиксированном (среднем) уровне других факторов, входящих в модель.

Для сравнения оценок роли различных факторов в формировании моделируемого показателя следует дополнить абсолютные величины относительными. Так, частные коэффициенты эластичности показывают, на сколько процентов в среднем изменяется у с изменением фактора х_j на один процент при фиксированном положении других факторов и рассчитываются по формуле:

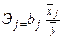, (5.10)

где b_j — коэффициент регрессии при j- м факторе.

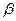— коэффициенты показывают, на какую часть среднего квадратического отклонения 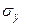изменится зависимая переменная у с изменением соответствующего фактора x_j на величину своего среднеквадратического отклонения 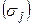. Этот коэффициент позволяет сравнивать влияние колеблемости различных факторов на вариацию исследуемого показателя, на основе чего выявляются факторы, в развитии которых заложены наибольшие резервы изменения результативного показателя:

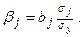(5.11)

Чтобы оценить долю влияния каждого фактора в суммарном влиянии факторов, включенных в уравнение регрессии, рассчитывают 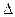-коэффициенты:

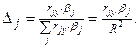(5.12)

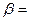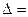Содержательный анализ моделей в целях уточнения приоритетности факторов опирается на сравнение перечисленных коэффициентов. В этих целях, особенно при достаточно большом числе факторов, включаемых в уравнение регрессии, производится ранжирование факторов по величине коэффициентов эластичности, и коэффициентов.

Рассмотрим принципы анализа степени влияния факторов на следующем примере, когда в уравнение регрессии были включены пять факторов.

Таблица 5.6

Факторы	Значения коэффициентов	Ранг факторов по величине коэффициентов	Средний ранг
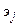
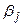
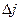
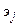
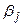
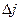
x1	0,17	0,20	0,16
x2	0,13	0,11	0,07
x3	0,10	0,14	0,10
x4	0,15	0,25	0,13
x5	1,79	0,73	0,52

Если сопоставить значения коэффициентов эластичности гр.2 и 5 табл.5.4, можно видеть, что главным фактором изменения результативного показателя является фактор х_5: при его изменении на 1% у возрастает на 1,79 %.Вторым по силе влияния на результативный показатель является фактор х₁ и т. д. (см. гр. 5 табл. 5.6).

Сравнение значений 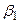позволяет сделать вывод о том, что с учетом уровня колеблемости факторов наибольшие резервы в изменении результативного показателя заложены в увеличении факторов х_5,х_4, и х₁ (см.гр.6 табл.5.6).

Сопоставление значений коэффициентов 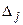позволяет сделать вывод, что наибольшая доля влияния приходится на фактор х₅: роль этого фактора в изменении результативного показателя составляет 52,0 % общего влияния пяти факторов на результативный показатель. Следовательно, наибольшие возможности в изменении результативного показателя связаны с изменением фактора х₅, затем фактора х₁ и т.д.

При построении многофакторных корреляционных моделей одной из предпосылок обоснованности конечных результатов является требование возможно меньшей коррелированности включенных в модель признаков-факторов (отсутствие мультиколлинеарности). Наличие взаимосвязи факторов затрудняет экономическую интерпретацию уравнения связи, так как изменение одного из факторов влечет, как правило, изменение факторов, с ним связанных. Для исключения мультиколлинеарности существует несколько методов. На практике чаще всего используют чисто эмпирический подход к решению этой проблемы. Более эффективным средством решения сформулированной выше задачи исключения коллинеарных факторов является использование факторного анализа.

Рассмотрим матрицу парных коэффициентов корреляции (индекс «0» присвоен результативному показателю у), по которой можно оценить степень взаимной коррелированности факторов.

Таблица 5.7

Факторы	у			…		…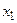
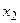
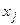
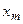
у				…		…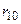
				…		…
				…		…
…	…	…	…	…		…	…
				…		…
…	…	…	…	…	…	…	…
				…		…

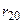
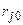
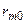
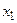
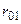
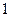
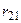
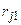
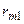
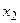
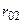
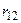
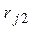
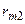
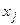
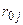
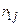
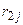
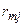
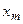
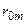
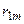
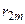
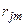
В качестве критерия мультиколлинеарности может быть принято соблюдение следующих неравенств:

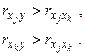(5.12)

Если приведенные неравенства (хотя бы одно из них) не выполняются, то исключается тот фактор х_j или x_k, связь которого с результативным показателем у будет менее тесной. Вместе с тем окончательный вывод о наличии или отсутствии мультиколлинеарности должен быть сделан в соответствии с экономическим содержанием и логикой взаимосвязи конкретных факторов.

Для более глубокого исследования связей между показателями целесообразно установить степень тесноты связи между результативным признаком у и каждым из факторов при исключении влияния других факторов.

Для решения поставленной задачи определяют коэффициенты частной корреляции, выявляющие степень «чистого» влияния фактора признака на результативный показатель. Для расчета частных коэффициентов корреляции могут быть использованы парные коэффициенты корреляции.

Для случая зависимости у от двух факторов необходимо вычислить два коэффициента частной корреляции:

1) частный коэффициент корреляции r_01,2 характеризует зависимость между результативным показателем и фактором х₁ при исключении влияния фактора х₂:

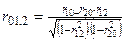_, (5.13)

2) второй частный коэффициент корреляции r_02.1 характеризует зависимость результативного признака от фактора х₂ при исключении влияния фактора х_1:

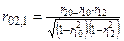_, (5.14)

Для общего случая частные коэффициенты корреляции можно определить по формуле:

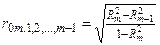, (5.15)

где 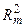— коэффициент детерминации результативного признака у с комплексом факторных признаков х_1,х_2,…,х_m-1,х_m;

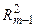— коэффициент детерминации результативного признака у с комплексом факторных признаков х_1,х_2,…,х_m-1;

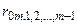— частный коэффициент корреляции у с факторным признаком х_m при исключении влияния факторных признаков х_1,х_2,…,х_m-1.

Многофакторные регрессионные модели используются в основном в двух направлениях — для сравнительного анализа и в прогнозировании.

Процедура сравнительного анализа с использованием уравнений регрессии сводится к следующему. Для каждой группы предприятий, сформированных по организационно-техническому уровню развития, находятся не только средние значения показателей, характеризующих эффективность деятельности, но и показателей, определяющих уровень результативных (под ними понимаются факторы, включенные в соответствующую регрессионную модель). Затем проводится сравнение средних значений факторов признаков сопоставляемых групп предприятий и определяются величины 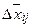, где j — номер; i — номер группы. Умножая разности 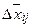, найденные по сравниваемым группам, на величину коэффициентов регрессии b_j в многофакторной регрессионной модели, получаем эффект влияния различий в уровнях факторов по группам (см.табл. 5.6) [11]. Величина полученного эффекта 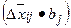позволяет судить о вкладе каждого фактора в изменение результативного показателя в данной группе по сравнению с другой группой.

Таблица 5.8

Общая схема сравнительного анализа с применением уравнений регрессии

Фак торы	Средние значения факторов по группе:	Разность средних значений факторов (гр.2-гр.3)	Коэф фициенты регрессии bj	Эффект влияния на результативный показатель различий в средних уровнях факторов (гр.4 * гр.5)
1группа	2 группа

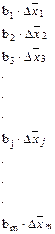
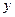
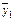
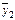
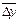
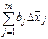
Общая величина различий значений результативного показателя 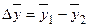в определенной части обусловлена изменением факторов, включенных в уравнение регрессии. Размер этого влияния определяется величиной 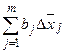. Разность (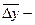 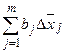) может быть объяснена влиянием прочих неучтенных факторов. Чем выше доля влияния включенных в уравнение регрессии факторов, тем большую значимость преобретает использование уравнения регрессии в управлении деятельностью исследуемой совокупности предприятий. По результатам такого сравнительного анализа можно дать обьективную оценку возможностей повышения эффективности производства и выявить внутрихозяйственные резервы.

Возможность широкого применения методов корреляционно- регрессионного анализа обусловлена сегодня широким распространением пакетов прикладных программ, таких как: «Harvard graphics», «Statgraf», «Supercalc», «Exel».

Дата добавления: 2014-12-10