
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Аналогия формул
|
|
|
|
Прямая задача кинематики для поступательного и вращательного движения.
Общий случай криволинейного движения
Способы задания движения. Уравнение движения
Физические модели
| Материальная точка | Пренебрегаем формами и размерами тела по сравнению с другими расстояниями в данной задаче | |
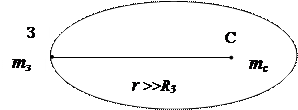
| ||
| Абсолютно твёрдое тело | Пренебрегаем деформацией |
| Способ |  Рисунок Рисунок
| Параметры и их связи | Уравнение движения |
| Векторный |
 – радиус-вектор – радиус-вектор

| 
| |
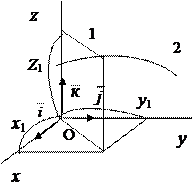 Координатный Координатный
| 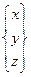 ПЛ координаты ПЛ координаты
 
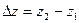


| Δ x = f 1 (t) Δ y = f 2 (t) Δ z = f 3 (t) | |
| Естественный | 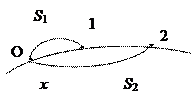
| s – КЛ координата Δ s = s 2 – s 1 | Δ s = f (t) |

| № п/п | Величина | Линейные величины | Угловые величины | Связь скалярных линейных и угловых величин | |||
| Векторные | Скалярные | Скалярные | |||||
| Путь (изменение положения тела) | |||||||
  перемещение по хорде
перемещение по хорде
| Δ S = S – S 0 (м) линейный путь по траектории | Δ φ = φ – φ 0 (pад) угловой путь | Δ S = Δ φ . R | ||||
| Скорость (изменение положения тела за единичный промежуток времени) | |||||||
| а) | средняя за большой промежуток времени | 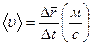 по хорде
по хорде
| 
| 
| 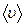 = = 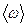 . R . R
| ||
 б) б)
| мгновенная за бесконечно малый промежуток времени | 
| 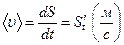
| 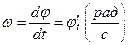
|  = ω . R = ω . R
| ||
| Ускорение – изменение скорости тела за единичный промежуток времени | |||||||
| а) | среднее | 
| 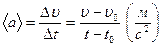
| 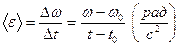
| 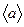 = =  . R . R
| ||
| б) | мгновенное |  внутрь кривизны (полное)
внутрь кривизны (полное) 
| 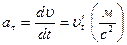
| 
| |||
| в) | тангенциальное (характеризует изменение υ по величине) | 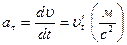 направлено
по касательной к траектории направлено
по касательной к траектории
| ατ = ε R | ||||
| г) | Нормальное (характеризует изменение υ по направлению) |  Направлено к центру кривизны
Направлено к центру кривизны
| αn = ω 2 R | ||||
| д) | полное | 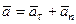
|  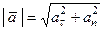
| ||||
|
|
|
|
|
Дата добавления: 2014-12-10; Просмотров: 473; Нарушение авторских прав?; Мы поможем в написании вашей работы!