Скалярные и векторные поля

Множество Е точек рассматриваемого пространства, совместно с приписанными этим точкам числами, называется скалярным полем. Скалярным полем часто называют и саму функцию F(M), породившую это поле на точечном множестве Е. Если Е – множество точек на плоскости, то скалярное поле называется плоским; если же Е – множество точек в трехмерном пространстве, то поле называется пространственным.

Примеры скалярных полей различной природы доставляет нам физика. Так, можно говорить о скалярном поле температур в пространстве, занятом нагретым телом (в каждой точке этого пространства температура имеет определенное значение); можно говорить о скалярном поле электрического потенциала в пространстве вокруг электрического заряда и т.п. Известные из физики изотермы (линии равной температуры), изобары (линии равного давления), эквипотенциальные линии (линии равного потенциала) являются примером линий уровня в различных плоских физических скалярных полях.

Для пространственного скалярного поля F(M) = F(x,y,z) уравнение F(x,y,z) = С с переменным параметром С определяет семейство поверхностей уровня, т.е. семейство поверхностей во всех точках каждойиз которых скалярное поле F(М) имеет одно и тоже значение. Поверхности уровня могут вырождаться в линии и точки. Для сферически симметричного поля, т.е. такого, что значение F(М) зависит только от расстояния точки М до некоторой фиксированной точки N, любая сфера с центром в точке N является поверхностью уровня. Если F(М) = const во всей области Е, то множество точек, удовлетворяющих уравнению F(x,y,z) = С, либо пусто, либо совпадает со всей областью Е.

Градиент скалярного поля u(M) = u(x,y,z) определяется равенством

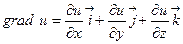. (1)

В математической теории поля широко используют символическое выражение, обозначаемое 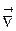("набла"): , напоминающее по формевектор, разложенный по базисным ортам 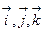, где вместо координат вектора записаны операторы дифференцирования 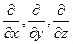. Это выражение называют векторным дифференциальным оператором или оператором Гамильтона.

Если каждой точке М данной области Е соответствует определенный вектор 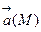, то говорят, что в области Е задано векторное поле. В декартовой системе координат векторное поле 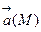задается тремя функциями P,Q,R, определенными в области Е

.

Здесь и в дальнейшем будем предполагать, что эти функции во всей области непрерывны вместе с частными производными. Для плоского векторного поля:

.

Векторной линией данного поля 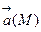называют такую линию ℓ, в каждой точке которой вектор 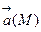имеет направление касательной к этой линии. Через каждую точку векторного поля проходит (при условии, что )одна векторная линия. Совокупность всех векторных линий определяется системой дифференциальных уравнений:

.

Векторные линии характеризуют векторные поля геометрически и дают известную информацию о структуре этого поля. Так, если 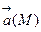– стационарное поле скоростей текущей жидкости, то в этом поле векторные линии, очевидно, будут являться траекториями частиц жидкости; называются они в таком случае линиями тока. В векторном поле 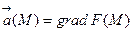векторные линии нормальны в каждой точке поверхностям уровня F(x,y,z) = С; вдоль этих линий функция F(M) изменяется быстрее всего. В случае плоского векторного поля семейство векторных линий определяется уравнением

.

Дата добавления: 2014-12-10