Поверхности уровня определяются уравнением

Примеры

1. Найти линии уровня плоского поля u=xy.

Решение. Линии уровня определяются уравнением xy=С и представляют собой равносторонние гиперболы. При С = 0 линиями уровня являются координатные оси Ох и Оу.

2. Найти поверхности уровня скалярного поля:

.

Решение. Поверхности уровня определяются уравнением . Отсюда находим . Мы видим, что поверхностями уровня являются круговые конусы x²+y²-a²z² = 0, ось симметрии которых совпадает с осью Оz.

3. Найти поверхности уровня скалярного поля:

.

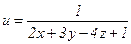Решение. Скалярное поле определено для всех точек пространства, кроме точек, расположенных на плоскости:

2x + 3y – 4z + 1 = 0

2x + 3y – 4z + 1 = С,

описывающим семейство параллельных плоскостей:

2x + 3y – 4z + С₁ = 0 (С₁ = 1 – С).

2. Найти поверхности уровня сферически симметричного поля:

Решение. Очевидно, что все сферы с центром в начале координат являются поверхностями уровня (при r=const и u=const). Для нахождения не просто поверхностей, на которых u=const, а всего множества точек с заданным значением поля, нужно решить уравнение cos r = C (–1 £ C £1).

Имеем: r = ± arccosC+2pn (n=0, ±1, ±2,…). Отбрасывая отрицательные значения r, найдем, что множество точек, для которых значение поля равно С, состоит из совокупности сфер радиусов arc cos c, arccos c + 2pn, -arccos c + 2pn, где n – целое число. Центры всех этих сфер совпадают с началом координат.

3. Найти градиент скалярных полей:

а) u(P)=x; б) u(P)=y; в) u(P)=z;

Решение. Применим формулу (1):

а) .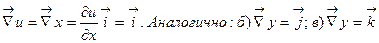

6. Найти градиент скалярного поля в точке М(2; 1).

Решение. По формуле (1): 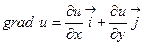. Вычислим частные производные в указанной точке: тогда: .

7. Найти

Решение. Пусть ; тогда

c учетом того, что 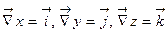получим .

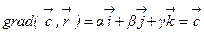8. Найти векторные линии поля .

Решение. Дифференциальные уравнения векторных линий в данном случае имеют вид:

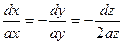
Интегрируя уравнение 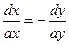, получимln |x|+ ln |y|= ln |c₁|, или xy=c₁. Решение уравнения 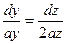приводит к результату 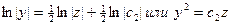. Следовательно, векторными линиями поля являются линии пересечения гиперболических цилиндров с параболическими:

9. Найти линии тока плоского потока жидкости, характеризуемого вектором скорости .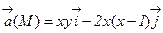

Решение. Интегрируя дифференциальное уравнение векторных линий в данном случае 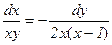, получим 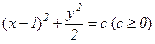. Это эллипсы с осями, параллельными осям координат, и с центром в точке (1, 0).

Дата добавления: 2014-12-10