Соленоидальное поле и его свойства

Векторное поле 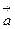(М) называют соленоидальным в области (G), если во всех точках этой области .

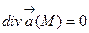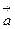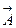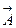С понятием соленоидального поля тесно связано понятие векторного потенциала. Если в области (G), в которой определено поле (М) существует такое векторное поле (М), что в каждой точке области (G) , то векторное поле (М) называют векторным потенциалом поля 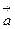(М) в области (G).

Для поля 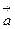(М), обладающего векторным потенциалом в области (G), поток через любую замкнутую поверхность, содержащуюся в области (G), равен нулю.

Поле 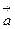(М), обладающее векторным потенциалом в области (G), является в ней соленоидальным. Обратное, вообще говоря, неверно: для произвольно взятой области (G) соленоидальность поля 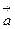(М) еще не гарантирует существования во всей области (G) векторного потенциала поля 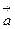(М). Однако, если ограничиться пространственно-односвязными областями, то соленоидальность поля и наличие у него векторного потенциала являются эквивалентными свойствами. Таким образом, в пространственно-односвязной области условие div 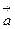= 0 является необходимым и достаточным для существования векторного потенциала.

Из формулы Остроградского-Гаусса следует, что если соленоидальное поле задано в односвязной области, то поток вектора через любую замкнутую поверхность, принадлежащую этой области, равен нулю:

.

Пусть соленоидальное поле 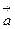задано в односвязной области. Тогда поток вектора 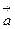через любую поверхность S, натянутую на заданный контур L, не зависит от вида этой поверхности, а зависит только от контура L.

Возьмем в поле 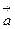замкнутый контур L и проведем через его точки векторные линии. Образовавшаяся поверхность называется векторной трубкой. Любая другая векторная линия, не проходящая через точки контура L, либо целиком лежит в векторной трубке, либо находится вне ее. В случае поля скоростей стационарного потока жидкостей векторная трубка – это та часть пространства, которую запасной при своем перемещении фиксированный объем жидкости.

Интенсивностью векторной трубки называется поток поля через поперечное сечение этой трубки. Для соленоидальных полей имеет место так называемый закон сохранения интенсивности векторной трубки.

Если соленоидальное поле 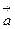определено в односвязной области G, то интенсивность векторной трубки постоянна вдоль всей трубки.

В соленоидальном поле векторные линии не могут ни начинаться, ни кончаться внутри поля; они либо замкнуты, либо имеют концы на границе поля, либо имеют бесконечные ветви (в случае неограниченного поля).

Дата добавления: 2014-12-10