Энергетические уровни водородоподобных атомов

Атом водорода, также ионизированный атом гелия(кот-го еще наз-ют водородоподобным атомом), явл-ся простейшими атомными системами. Потенц-ая энергия водородоподобного атома равна:

U(r)=- Ze²/r, поэтому Ур-ие Шредингера для нахождения состояний электрона в таком атоме имеет след вид:

(-ħ²/2m)∆ψ- (Ze²/r)ψ= Eψ

Оператор Лапласа выражают ∆=d²/dr² + 2d/rdr. Тогда Ур-ие Шредин-ра имеет вид:

-ħ²/2m (d²ψ/dr² + 2dψ/rdr) – (Ze²/r)ψ = Eψ. Из этого Ур-ия можно получить возможные собс-ые значения оператора энергии: E= (-Z²R1)/ n². Из выражения следует что энергии электрона в водородоподобном атоме как и у частицы в потенц-ой яме также явл-ся дискретными.

№24. Линейный гармонический осциллятор – система, совершающая одномерное движение под действием квазиупругой силы, является моделью, которая часто используется при описании классических и квантовых систем. Пружинный, физический и математический маятники – примеры классических гармонических осцилляторов. Потенциальная энергия гармонического осциллятора равна: U= , где

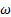- собственная частота колебаний осциллятора. m – масса частицы.

Гармонический осциллятор в квантовой механике – квантовый осциллятор – описывается уравнением Шредингера вида + 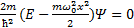, где

E - полная энергия осциллятора. Рис4

Собственные значения энергии для этого уравнения: 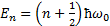(n=0,1,2,…)

Таким образом, энергия квантового осциллятора квантуется (может иметь лишь дискретные значения). Уровни энергии расположены на одинаковых расстояниях, равных . Минимальная энергия называется энергией нулевых колебаний. Существование энергии нулевых колебаний – типично квантовый эффект – прямое следствие соотношение неопределенностей. Частица в яме любой формы не может находиться на ее дне, поскольку в нуль обращается импульс частицы и его неопределенность, а неопределенность координаты становится бесконечной, что противоречит, в свою очередь, условию пребывания частицы в “потенциальной яме “.

Правилами отбора в квантовой механике называются условия, накладываемые на изменения квантовых чисел.

Для гармонического осциллятора возможны лишь переходы между соседними подуровнями, т.е. переходы, удовлетворяющие правилу отбора: . Следовательно, энергия гармонического осциллятора может изменяться только порциями и гармонический осциллятор испускает и поглощает энергию квантами.

Квантово-механическое решение задачи о квантовом осцилляторе показывает, что имеется отличная от нуля вероятность, обнаружить частицу за пределами области . Cуществование отличных от нуля значений вероятности обнаружения частицы за пределами потенциальной ямы объясняется возможностью прохождения микрочастиц сквозь потенциальный барьер.

На рис 5 приведена квантовая плотность вероятности обнаружения осциллятора при , имеющая конечные значения для .

№25 Связь между квантовыми числами. Изучение атомных орбиталей, рассчитанных с помощью уравнения Шредингера, показало, что характер движения электрона в атоме определяется четырьмя числами - п, l, m, s, получившими общее название квантовых чисел: главное, орбитальное, магнитное и спиновое.

Главное квантовое число n. Это число может принимать любые положительные целочисленные значения: n = 1, 2, 3. Определяет орбитальный радиус и соответствующий главный энергетический уровень E_n. Совокупность атомных орбиталей с одинаковым значением главного квантового числа n составляют одну электронную оболочку.

Орбитальным радиусом r_орб называют расстояние от ядра атома до наиболее удаленной точки поверхности, изображающей атомную орбиталь. Для сферической поверхности орбитальный радиус равен радиусу сферы. Для поверхности в виде песочных часов орбитальный радиус равен диаметру одной из составляющих сфер (рис. 3.1).

Главным энергетическим уровнем называют часть энергии атома, определяемой главным квантовым числом п.

Рис. 3.1. Определение орбитального радиуса r_орб для атомных орбиталей разной формы: а - s-орбитали; б - _р-орбитали

Энергия притяжения между электроном и ядром уменьшается обратно пропорционально квадрату главного квантового числа n², а орбитальный радиус r_орб увеличивается пропорционально этой величине. С увеличением числа п электрон в среднем находится все дальше от ядра. При п →∞ энергия притяжения становится равной нулю, электрон отрывается от ядра. Происходит ионизация атома.

Таким образом, главные энергетические уровни Е_п атома можно определять экспериментально измерением минимальной энергии, необходимой для отрыва электрона от атома. Определяемая таким способом величина называется энергией ионизации атома - I. Это очень важная характеристика атома, от которой зависят его свойства, в частности электроотрицательность. Е_п уменьшается с возрастанием главного квантового числа п и орбитального радиуса r_орб.

Орбитальное квантовое число l. Число l может принимать целочисленные значения: l = 0, 1, 2, п - 1, т.е. максимальное значение l не превышает п - 1, где п - главное квантовое число.

Величина l определяет форму атомной орбитали и орбитальный подуровень энергии E_nl - главного энергетического уровня атома при данном п. При l = 0 форма орбитали сферическая и называется s-орбиталью. При l = 1 орбиталь имеет форму песочных часов (гантели) и называется р-орбиталью. При l = 2 форма орбитали четырехлопастная и называется d-орбиталью.

У р-орбиталей имеется узел, а у d-орбиталей узловые плоскости, где волновые функции равны нулю. Знаки лопастей чередуются. При п = 1 имеется только одна s-орбиталь и отсутствуют другие подуровни энергии и орбитали. При п = 2 имеются 2s (l = 0)- и 2р (l = 1)-орбитали разной ориентации. Им соответствуют энергетические подуровни Е_2s" Е_2р. При п = 3 имеются одна 3s (l = 0)-, 3р (l = 1)- и 3d (l = 2)-орбитали разных ориен-таций. Им соответствуют энергетические подуровни E_3s, Е_3p' E_3d.

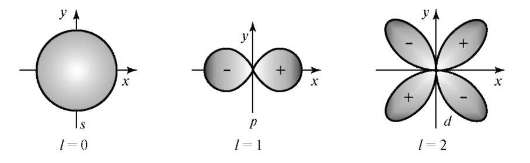
Рис. 3.2. Пространственная форма s-, p-, d-атомных орбиталей

Размер атомных орбиталей разной формы возрастает с увеличением п.

Магнитное квантовое число m. Число т принимает целочисленные значения: 0, ±1, ±2, ±l. Определяют ориентацию орбиталей в пространстве, их число на данном орбитальном подуровне E_nl и магнитный энергетический подуровень E_nlm. На каждом орбитальном подуровне Е (l = 1) имеется три п_р-орбитали с ориентацией вдоль осей х, у, z. Например, при п= 2 подуровню E_2l(l = 1) соответствуют орбитали 2р_х(m = ±1), 2р_у(m = -1) и 2р_z(m = 0) (рис. 3.3).

При п = 3 подуровню Е₃₁ (l = 2) отвечают пять орбиталей разных ориентаций.

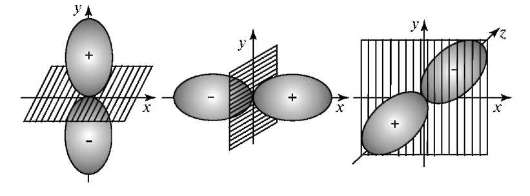
Рис. 3.3. Ориентация р-атомных орбиталей при разных значениях магнитного квантового числа т

Спиновое квантовое число s. Число s принимает два значения: +0,5 и -0,5. Характеризует собственное вращательное движение электрона. На каждой атомной орбитали двум значениям S = ± 0,5 отвечает вращение по часовой и против часовой стрелки. Соответственно имеются два спиновых подуровня энергии E_nlms.

Четыре квантовых числа n, l, m, s характеризуют различные типы пространственного квантования при движении одного электрона в атоме и определяют соответствующие квантовые энергетические уровни.

Орбиталь φ_nlm и соответствующий энергетический уровень E_nlm, определяемый четырьмя квантовыми числами п, l, m, s, называют квантовым состоянием электрона в атоме.

№26 Спин электрона, протона и элементарных частиц Спин был обнаружен в экспериментах Штерна и Герлаха (рис 1) при прохождении узкого пучка атомов водорода, находящихся в s - состоянии через сильное неоднородное магнитное поле. В этом состоянии l =о, момент импульса и магнитное поле не должно было влиять на движение атомов. Однако пучок атомов расщепляется на два пучка, следовательно, было обнаружено пространственное квантование механического момента, не связанного с орбитальным движением электрона.

Спин электронов и всех других микрочастиц следует рассматривать как внутреннее неотъемлемое квантовое свойство микрочастицы: подобно тому как частицы имеют массу, а заряженные частицы имеют заряд, они имеют еще и спин. Спин 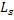, как механический момент, квантуется по закону:

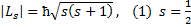- спиновое квантовое число.

С ним связан собственный магнитный момент . (2).

Проекция 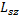может принимать 2s+1 ориентаций. Так как опыты Штерна и Герлаха обнаружили только две ориентации спина, то 2s+1=2, откуда: .

Проекция , где 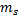- магнитное спиновое квантовое число, которое может иметь только два значения:

Спин – это квантовая величина, не имеющая классического аналога.

Таким образом, состояние электрона в атоме определяется набором четырех квантовых чисел: главного n (n=1,2,3,…..)

oрбитального l (l=0,1,2,…n-1)

магнитного m (m=-l,…0, +l)

магнитного спинового ()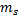

Вот уже более 25 лет физики пытаются ответить на вопрос о спиновой структуре протона.

Известно, что протон состоит из трех кварков. И первоначально ученые предполагали, что спин протона был суммой спинов трех составляющих его кварков. Но в 80-е годы прошлого столетия экспериментальным путем было выяснено: вклад кварков в суммарный спин протонов частичен. Тогда откуда берется остальная часть спина протона? В этом вопросе и суть так называемого кризиса спина протона («спиновой загадки»), над которой ученые бьются до сих пор. До настоящего времени было выдвинуто предположение, что появлению спина способствуют глюоны, которыми соединяются кварки внутри протона. Эту идею поддерживает ряд исследований на Релятивистском коллайдере тяжелых ионов (RHIC) в Брукхейвенской национальной лаборатории в Аптоне (штат Нью-Йорк). В ходе этих исследований анализируются столкновения протонов.

Дата добавления: 2014-12-16