Электростатика

Электрический заряд.

Электричество как особый вид материи изучалось еще древними греками, но количественная мера его - электрический заряд – была введена лишь после опытов Кулона. Электрический заряд является неотъемлемым свойством многих элементарных частиц. Наименьший заряд, известный в настоящее время, равен 1,6·10 ^–19 Кулона.

Установлено, что суммарная величина электрического заряда в замкнутой системе остается постоянной. Это положение носит название закона сохранения заряда.

Существуют два различных типа электрических зарядов, один из которых условно был назван положительным, а другой – отрицательным. Субъективный характер выбора такого названия привел к тому, что заряд электрона оказался отрицательным. Это привело к некоторой путанице в определении направления электрического тока, но на первой стадии изучения электричества нас будут интересовать неподвижные заряды, обычно называемые статическими.

Закон Кулона.

Еще из школьного курса физики известно, что электрические заряды взаимодействуют друг с другом. Величина силы взаимодействия измерена Кулоном, и закон, характеризующий силу взаимодействия двух статических точечных зарядов Q и q, носит его имя. Сила взаимодействия между зарядами прямо пропорционально величине этих зарядов и обратно пропорциональна квадрату расстояния между ними.

Если учесть, что сила – это вектор, то этот закон может быть записан в таком виде:

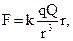
где r /r – единичный вектор, направленный вдоль прямой, соединяющей оба заряда, расстояние между которыми равно r.

Коэффициент k вводится в связи с использованием определенной системы единиц. В принятой у нас системе СИ этот коэффициент выражается через так называемую диэлектрическую постоянную вакуума ε₀ = 8,86 · 10 ^–12 Ф/М (k = 1/ 4π ε₀). Причиной появления этого коэффициента является выбор единицы измерения заряда – в системе СИ заряд измеряется в Кулонах, являющихся производными единицами (основной единицей служит Ампер – единица измерения силы тока).

Характеристики электрического поля.

Напряженность электрического поля.

Любое взаимодействие тел, находящихся на некотором расстоянии друг от друга, осуществляется посредством поля. Применительно к электрическим зарядам это означает, что вокруг любого заряда существует особый вид материи – электрическое поле. Это поле не воспринимается непосредственно чувствами человека. Для обнаружения поля используются другие заряды, называемые пробными. Однако, из закона Кулона следует, что величина силы воздействия на пробный заряд зависит от величины этого заряда. Для характеристики самого поля вводится величина силы, действующей на пробный заряд, отнесенная к величине этого пробного заряда. Эта величина называется напряженностью электрического поля. Другими словами можно сказать, что напряженность электрического поля есть сила, действующая на единичный положительный заряд, помещенный в данную точку поля (единицы измерения - Вольт/метр).Если обозначить заряд, поле которого мы изучаем – Q, то напряженность поля в любой точке пространства вокруг этого заряда, находящейся на расстоянии r от него, равна:

E=(1/4pe) (Qr) /r³; E = (1/4pe)(Q/r²).

Напряженность поля от нескольких зарядов находится по принципу суперпозиции: напряженность поля от суммы зарядов равна сумме всех напряженностей от каждого заряда в отдельности, т.е. E (Σ Q_i) = Σ (E_i).

Этот принцип позволяет находить напряженность поля от любых зарядов, распределенных в пространстве, причем, вместо суммы используются интегралы. Однако вычисление осложняются тем, что напряженность поля – вектор. Поэтому часто приходится сначала вычислять отдельные составляющие вектора Е, а общую величину находить их суммированием. Для прямоугольной системы координат это делается сравнительно просто:

E² = E_x² + E_y² +E_z².

Принцип суперпозиции позволяет вычислить напряженность поля от любой конфигурации зарядов, представив ее как некую сумму бесконечно малых (точечных) зарядов. Дело лишь в том, как проводить суммирование (интегрирование). Для рассмотренного одномерного случая это простой интеграл. Для распределения зарядов по поверхности это будет двумерный (поверхностный) интеграл, для объемного распределения – трехмерный (объемный) интеграл. Для наглядного представления электрическое поле принято изображать в виде линий, названных силовыми. Под силовыми линиями понимаются линии, касательные к которым в данной точке совпадают с направлением вектора напряженности в этой точке. Кроме того, было условлено, что густота силовых линий должна быть пропорциональна величине напряженности. Силовые линии начинаются на положительных и кончаются на отрицательных зарядах. Картина силовых линий от двух точечных зарядов изображена на рис.

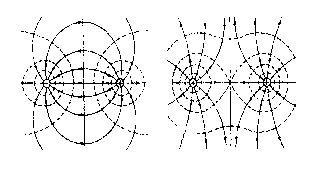Как видно из рисунка, в промежутке между зарядами силовые линии являются непрерывными. Это означает, что направление векторов напряженности во всех точках однозначно, т.к. линии нигде не пересекаются. Для количественного описания силовых линий вводится понятие потока.

Потоком вектора напряженности через заданную поверхность называется скалярное произведение вектора напряженности на величину этой поверхности: Ф = (ЕS).

При этом предполагается, что поверхность - это вектор, причем направление этого вектора определяется направлением внешней нормали n к поверхности, т.е. нормали, проведенной в сторону выпуклости поверхности: dФ = (E dS) = EdS cosa = E_n dS. Для плоской поверхности направление внешней нормали должно задаваться дополнительными условиями.

Теорема Гаусса.

Дата добавления: 2014-12-16