
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Векторная алгебра
|
|
|
|
Теория неявных функций и ее приложения.
Функции нескольких переменных.
Определенный интеграл.
Интегрирование в элементарных функциях.
Комплексные числа. Алгебра многочленов.
Неопределенный интеграл.
1. Понятие первообразной функции. Основные свойства неопределенного интеграла.
Таблица основных неопределенных интегралов.
2. Интегрирование подстановкой и по частям
3. Комплексные числа. Многочлены, корни многочленов. Кратные корни. Признак кратности корня.
4. Выделение кратных корней. Алгоритм Евклида деления многочлена на многочлен. Разложение правильной рациональной дроби на сумму простейших.
5. Интегрирование рациональной дроби
6. Интегральные суммы. Верхние и нижние интегральные суммы.
7. Необходимое и достаточное условие интегрируемости. Свойство равномерной непрерывности функций. Интегрируемость непрерывных функций. Интегрируемость некоторых разрывных функций.
8. Основные свойства определенного интеграла. Оценки интегралов. Формулы среднего значения.
9. Существование первообразной для непрерывной функции. Основная формула интегрального исчисления. Замена переменной под знаком интеграла.
4. Геометрические и физические приложения определенного интеграла.
10. Длина дуги кривой. Примеры.
11. Площадь плоской фигуры. Примеры.
12. Объемы тел. Площадь поверхности вращения.
13. Физические приложения: масса и центр тяжести, работа силы.
14. Понятие функции нескольких (2 и 3) переменных. Понятие m -мерного координатного пространства. Понятие функции m переменных.
15. Предельное значение функции нескольких переменных.
16. Непрерывные функции нескольких переменных.
17. Частные производные функций нескольких переменных.
18. Дифференциалы функций нескольких переменных. Градиент.
19. Частные производные высших порядков. Формула Тейлора для функции нескольких переменных.
20. Локальный экстремум функции нескольких переменных.
21. Понятие о неявной функции. Теорема о существовании и дифференцируемости неявной функции.
22. Неявные функции, определяемые системой функциональных уравнений. Взаимно однозначное отображение двух множеств m -мерного пространства.
23. Зависимость функций. Якобиан.
24. Условный экстремум. Метод неопределенных множителей Лагранжа.
Рекомендуемая литература
7. Ильин В.А., Позняк Э.Г. Основы математического анализа. М., Наука, 1965.
8. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. М., Наука, 1969.
9. Курант Р. Курс дифференциального и интегрального исчисления. М., Наука, 1967.
10. Демидович Б.П. Сборник задач и упражнений по математическому анализу. СПб., Мифрил, 1995.
11. А.М.Тер-Крикоров, М.И.Шабунин. Курс математического анализа, М., МФТИ, 1997.
6. Вавилов В.В., Мельников И.И. и др. Задачи по математике. Начала анализа: справочное пособие. М., Наука, 1990.
Таблица неопределенных интегралов некоторых функций.
1. 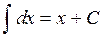
2. 
3. 
4. 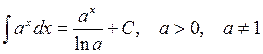
5. 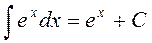
6. 
7. 
8. 
9 
10. 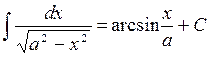
11. 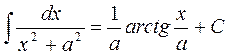
12. 
Контрольное задание
Вариант 1.
Найти:
1)  2)
2)  3)
3) 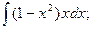 4)
4) 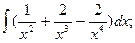
5)  6)
6)  7)
7) 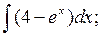 8)
8) 
9) 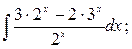 10)
10)  11)
11) 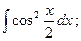
12)  13)
13)  14)
14) 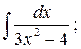 15)
15) 
16) 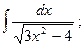 17)
17)  18)
18)  19)
19) 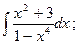
20) 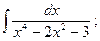
1. Найти площадь фигуры, заданной неравенством:
1.1.  1.2.
1.2. 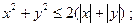
2. Найти площадь фигуры, ограниченной графиком функции
2.1. 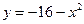 и касательными к этой параболе, проведенными из начала координат.
и касательными к этой параболе, проведенными из начала координат.
2.2.  касательной к графику этой функции в точке
касательной к графику этой функции в точке 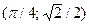 и прямыми
и прямыми 
3. Найти площадь фигуры, ограниченной графиками функций  и прямыми
и прямыми 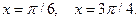
4. Фигура ограничена графиком функции  и прямыми
и прямыми  Под какими углами к оси ОХ надо провести прямые через точку (0; 0), чтобы они разбили фигуру на три равновеликие части?
Под какими углами к оси ОХ надо провести прямые через точку (0; 0), чтобы они разбили фигуру на три равновеликие части?
Вариант 2
Найти:
1) 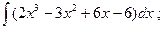 2)
2) 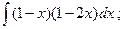 3)
3) 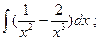
4)  5)
5)  6)
6) 
7)  8)
8)  9)
9) 
10) 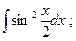 11)
11)  12)
12)  13)
13) 
14)  15)
15) 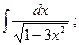 16)
16) 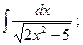 17)
17) 
18) 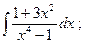 19)
19) 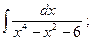 20)
20) 
1) Найти площадь фигуры, заданной неравенством:
1.1  1.2.
1.2. 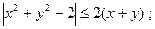
2) Найти площадь фигуры, ограниченной графиком функции:
2.1.  и касательными к графику этой функции
и касательными к графику этой функции
в точках (1; 1/2) и (4; 2);
2.2.  и касательной к графику функции
и касательной к графику функции  в точке (1; 3);
в точке (1; 3);
3) Найти площадь фигуры, ограниченной графиком функции  и прямыми
и прямыми 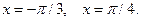
4) Фигура ограничена графиком функции  и прямыми
и прямыми 
Под какими углами к оси ОХ надо провести две прямые через точку (0; 9), чтобы они разбили фигуру на три равновеликие части?
Вариант 3
Найти:
1) 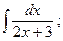 2)
2)  3)
3) 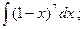 4)
4) 
5) 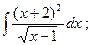 6)
6) 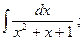 7)
7) 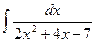 ; 8)
; 8) 
9)  10)
10) 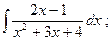 11)
11)  12)
12) 
13)  14)
14) 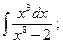 15)
15) 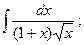 16)
16) 
17)  18)
18)  19)
19)  20)
20) 
21)  22)
22)  23)
23)  24)
24) 
Найти площадь фигуры, ограниченной графиками функций:
1) y=x2 и y=x+2; 2) y=x2-2x+3 и y=3x-1; 3) y=x2 и y=1+3x2/4;
4) y=2/x и y=-x/2-5/2; 5) y=(6x2-x4)/9 и y=1; 6) y=x3 и 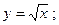
7) 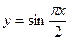 и y=x2; 8)
и y=x2; 8) 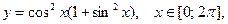 и y=0;
и y=0;
9)  и
и  10)
10) 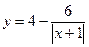 и
и 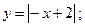
Рабочая программа по курсу «Аналитическая геометрия и линейная алгебра»
Лектор: Сахаров Я.А.
Часть I. Аналитическая геометрия
1.Решение систем линейных уравнений. Определители 2го и 3го порядка. Формулы Крамера.
Операции над матрицами. Обратная матрица, существование и вычисление.
2. Понятие вектора. Линейные операции над векторами. Линейная зависимость векторов.
3. Базис на плоскости и в пространстве. Разложение вектора по базису. Системы координат на плоскости и в пространстве. Преобразован6ие декартовой системы координат на плоскости и в пространстве.
4. Скалярное произведение векторов. Векторное, смешанное и двойное векторное произведение. Вычисление этих произведений в прямоугольных декартовых координатах.
Линейные образы: прямая на плоскости, прямая и плоскость в пространстве
5. Различные типы уравнений прямой на плоскости. Задачи на прямую на плоскости.
6. Различные типы уравнений плоскости.
7. Прямая и плоскость в пространстве, угол между прямыми и плоскостями. Задачи на взаимное положение прямой и плоскости.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 475; Нарушение авторских прав?; Мы поможем в написании вашей работы!