Билинейные и квадратичные формы

Линейные отображения векторных пространств

Линейные (векторные) пространства

Системы линейных уравнений. Матрицы

Канонические уравнения кривых и поверхностей второго порядка

8. Линии второго порядка. Определение линий второго порядка, как геометрического места точек. Канонические уравнения эллипса, гиперболы, параболы.

9. Исследование линий второго порядка, инварианты, стандартные методы упрощения уравнений кривых второго порядка.

10. Канонические уравнения поверхностей второго порядка.

Рекомендуемая литература

Ильин В.А., Позняк Э.Г., Аналитическая геометрия, М., Наука, 1988.

Беклемишев Д.В., Курс аналитической геометрии и линейной алгебры, М, Наука, 1984.

Канатников А.Н., Крищенко А.П., Аналитическая геометрия, М., Изд. МГТУ им. Н.Э. Баумана, 1999.

Бахвалов С.В., Моденов П.С., Пархоменко А.С., Сборник задач по аналитической геометрии, М., Наука, 1976.

Клетеник Д.В., Сборник задач по аналитической геометрии, М., Наука, 1975.

Ефимов А.В., Каракулин А.Ф. и др., Сборник задач по математике для втузов, ч.1, М., Физматлит, 2001.

Часть II. Линейная алгебра

1. Определитель n^го порядка, определение по индукции. Свойства определителя.
2. Миноры, дополнительные миноры и алгебраические дополнения. Вычисление определителя разложением по строке (столбцу). Теорема Лапласа.
3. Правило Крамера для систем n^го порядка.
4. Метод исключения Гаусса.
5. Ранг матрицы, базисный минор, линейная зависимость строк матрицы.
6. Операции над матрицами. Умножение матриц.
7. Присоединенная и обратная матрица.
8. Системы линейных однородных уравнений. Фундаментальная система решений.
9. Общая теория систем линейных уравнений. Теорема Кронеккера-Капелли. Решение произвольной системы линейных уравнений.

1. Определение линейных пространств. Базис линейного пространства.
2. Конечномерные линейные пространства. Разложение вектора по базису. Связь между базисами, матрица перехода. Преобразование координат вектора.
3. Скалярное произведение. Евклидовы пространства. Длина вектора и угол между векторами. Неравенство Коши – Буняковского.
4. Ортогональный и ортонормированный базисы. Процесс ортогонализации. Ортогональное дополнение подпространства.

1. Определение линейного отображения, свойства, примеры. Матрица линейного отображения. Ядро и образ линейного оператора. Ранг и дефект.
2. Действия над линейными операторами. Существование обратного оператора.
3. Инвариантные подпространства. Собственные векторы и собственные числа. Характеристический многочлен. Теорема Гамильтона-Кэли.

1. Определение, матрицы. Теорема Лагранжа. Закон инерции.
2. Положительно определенные квадратичные формы. Критерий Сильвестра.
3. Приведение квадратичной формы к каноническому (нормальному) виду.

Рекомендуемая литература

Ильин В.А., Позняк Э.Г., Линейная алгебра, М., Наука, 1988.

Беклемишев Д.В., Курс аналитической геометрии и линейной алгебры, М, Наука, 1984.

Канатников А.Н., Крищенко А.П., Линейная алгебра, М., Изд. МГТУ им. Н.Э. Баумана, 1999.

Курош А.Г. Курс высшей алгебры, М., Наука, 1971.

Проскуряков И.В. Сборник задач по линейной алгебре, М., Наука, 1978.

Ефимов А.В., Каракулин А.Ф. и др., Сборник задач по математике для втузов, ч.1, М., Физматлит, 2001

Задание по курсу «Аналитическая геометрия»

1. Вычислить определитель матрицы

Вариант 1 Вариант 2 Вариант 3

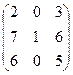
1. Решить систему уравнений

Вариант 1	Вариант 2	Вариант 3
x1 + 2x2 + 3x3 + 4x4 = 5	2x1 + 2x2 - x3 + x4 = 4	2x1 + 3x2 + 11x3 + 5x4 = 2
2x1 + x2 + 2x3 + 3x4 = 1	4x1 + 3 x2 - x3 + 2x4 = 6	x1 + x2 + 5x3 + 2x4 = 1
3x1 + 2x2 + x3 + 2x4 = 1	8x1 + 5x2 - 3x3 + 4x4 = 12	2x1 + x2 + 3x3 + 2x4 = - 3
4x1 + 3x2 + 2x3 + x4 = - 5	3x1 + 3x2 - 2x3 + 2x4 = 6	x1 + x2 + 3x3 + 4x4 = - 3

1. Найти обратную матрицу методом элементарных преобразований

Вариант 1

Вариант 2

Вариант 3

1. Даны три вектора p = {3; -2; 1}, q = {-1; 1; -2}, r = {2; 1; -3}

Найти разложение вектора c по базису p, q, r.

Вариант 1

Вариант 2

Вариант 3

c = {11; -6; 5} c = {9; -6; 4} c = {-7; -7; 5}

1. Даны три некомпланарных вектора a, b, c

Вычислить, при каких значениях λ и μ векторы

	λa + b + c, a +λb + c, a + b +λcкомпланарны	Вариант 1
	λa +μb + c, a +λb +μcколлинеарны	Вариант 2
	a + b, b + c, a -λcкомпланарны	Вариант 3

1. Составить каноническое уравнение прямой

Вариант 1

Вариант 2

Вариант 3

1. Доказать параллельность прямых

Вариант 1

Вариант 2

Вариант 3

x = 4t + 5; y = – 2t + 2; z = 2t – 7;	x = 2t + 5; y = – t + 2; z = t – 7;	x = t + 3; y = t + 4; z = – 2t + 6;
и	и	и

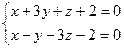
1. Составить уравнение плоскости, проходящей через прямую

Вариант 1	Вариант 2	Вариант 3
параллельно векторуl{2,-1,-2}	и точку М{4,-2,-3}	Перпендикулярно плоскости x – 2y + z + 5 = 0

1. Даны вершины треугольника А (4, 1, - 2); В (2, 0, 0); С (-2, 3, -5)

Составить уравнение высоты и найти длину высоты, опущенной из вершины

Вариант 1	Вариант 2	Вариант 3
А	В	С

1. При каких значениях m и n уравнение определяет:

1. Центральную линию;
2. Линию без центра;
3. Линию, имеющую бесконечно много центров.

Вариант 1	x^2 + 6xy + my^2 + 3x + ny – 4 = 0
Вариант 2	mx^2 + 12xy + 9y^2 + 4x + ny – 13 = 0
Вариант 3	5x^2 + 14xy + my^2 + 20x + ny – 18 = 0

1. Привести уравнение к каноническому виду, определить тип уравнения, определить геометрический образ, определяемый уравнением. Построить на чертеже оси первоначальной системы координат, оси систем, которые вводятся по ходу решения, и геометрический образ, определяемый уравнением. Определить параметры кривой (если они существуют): полуоси, эксцентриситет, координаты фокусов, выписать уравнения директрис и асимптот.

Вариант 1	4xy + 3y^2 + 16x + 12y – 36 = 0
Вариант 2	3x^2 + 10xy + 3y^2 – 2x – 14y – 13 = 0
Вариант 3	25x^2 – 14xy + 25y^2 + 64x – 64y – 224 = 0

Задание по курсу «Линейная алгебра»

1) Найти размерности и базисы суммы и пересечения подпространств

L₁ = < a₁, a₂, a₃ > и L₂ = < b₁, b₂, b₃ >, если:

Вариант 1	a1 = (1, 2, 1) ^T	b1= (2, 3, -1) ^T
	a2 = (1, 1, -1) ^T	b2 = (1, 2, 2) ^T
	a3 = (1, 3, 3) ^T	b3 = (1, 1, - 3) ^T
Вариант 2	a1 = (1, 2, 1,-2) ^T	b1= (1, 1, 1, 1) ^T
	a2 = (2,3,1,0) ^T	b2 = (1, 0,1,-1) ^T
	a3 = (1, 2,2,-3) ^T	b3 = (1, 3,0, - 4) ^T
Вариант 3	a1 = (1, 1,0,0) ^T	b1= (1,0,1, 0) ^T
	a2 = (0,1, 1, 0) ^T	b2 = (0,2,1,1) ^T
	a3 = (0,0,1,1) ^T	b3 = (1, 2,1,2) ^T

2). Разложить вектор X на суммудвух векторов, один из которых лежит в подпространстве, натянутом на векторы a₁, a₂, a₃, а другой ортогонален к этому подпространству.

Вариант 1	X = (-3, 5, 9, 3) ^T
a1 = (1, 1, 1, 1) ^T	a2 = (2, - 1, 1, 1) ^T	a3 = (2, - 7, - 1, - 1) ^T
Вариант 2	X = (2,- 5, 3,4) ^T
a1 = (1, 3, 3, 5) ^T	a2 = (1, 3, -5, -3) ^T	a3 = (1, -5, 3, - 3) ^T
Вариант 3	X = (5, 2, - 2, 2) ^T
a1 = (2, 1, 1, - 1) ^T	a2 = (1, 1, 3, 0) ^T

3) Если линейный оператор φ, действующий в пространстве L _n, имеет n линейно независимых собственных векторов e₁, e₂, … e_n, соответствующих собственным числам λ₁, λ₂, …..λ_n, то в базисе из этих векторов матрица оператора имеет диагональный вид с диагональными элементами, равными собственным числам.

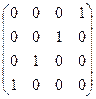
Для заданной матрицы оператора найти этот базис и соответствующую ему диагональную форму матрицы.

Вариант 1	Вариант 2	Вариант 3

4). Линейный оператор φ переводит векторы a₁, a₂, a₃ соответственно в векторы b₁, b₂, b_3.

Найти матрицу оператора φ в том же базисе, в котором заданы координатами все векторы:

Вариант 1	a1 = (1, 2, -3) ^T	a2 = (0, 1, 2) ^T	a3 = (1, 0, 4) ^T
	b1= (1, 1, 1) ^T	b2 = (1, 2, 1) ^T	b3 = (0, 1, 1) ^T
Вариант 2	a1 = (1, 2, 1) ^T	a2 = (4, 3, - 2) ^T	a3 = (- 5, - 4, - 1) ^T
	b1= (1, 1, 1) ^T	b2 = (1, 0, 1) ^T	b3 = (0, - 1, 1) ^T
Вариант 3	a1 = (1, 1, 1) ^T	a2 = (2, - 3, 1) ^T	a3 = (4, 1, - 5) ^T
	b1= (0, 1, 0) ^T	b2 = (0, 1, 1) ^T	b3 = (1, 1, 0) ^T

5). Преобразовать к каноническому виду ортогональным преобразованием квадратичную форму и выписать преобразование координат

Вариант 1	x1^2+ 2x2^2 + 3x3^2- 4x1x2 - 4x2x3
Вариант 2	3x1^2- 8x1x2 -3x2^2- x3^2+ 4x3x4 - 4x4^2
Вариант 3	4x1^2+ 4x1x2 - 12x1x3 - 6x2x3 + x2^2+ 9x3^2

ОСТАПЕНКО А.А., САХАРОВ Я.А.

Дата добавления: 2014-12-16