Дерево достижимости

Методы анализа

Ограниченность

Безопасность – это частный случай более общего свойства ограниченности. Некоторые соображения относительно реального ограничения на аппаратную, реализацию позиций позволяют прийти к заключению, что безопасность – необязательное требование. Безопасность позволяет реализовать позицию триггером, но в более общем случае можно использовать счётчик. Однако любой аппаратно реализованный счётчик ограничен по максимальному числу, которое он может представить. Позиция является k -безопасной или k -ограниченной, если количество фишек в ней не может превышать целое число k.

Определение 11. Позиция p_i Î P сети Петри С = (Р, Т, I, O) с начальной маркировкой m является k -безопасной, если m'(p_i) £ k для всех m' Î R(C, m).

Иногда нас будет интересовать только то, является число фишек в позиции ограниченным или нет, а не конкретное значение границы. Позиция называется ограниченной, если она k– безопасна для некоторого k; сеть Петри ограниченна, если все её позиции ограниченны. Ограниченную сеть Петри можно реализовать аппаратно, тогда как сеть Петри с неограниченными позициями в общем случае реализовать аппаратно нельзя.

В этом разделе мы представим два основных метода анализа сетей Петри, которые описывают механизмы решения некоторых из уже перечисленных задач. Первый метод анализа, используемый для сетей Петри, – это дерево достижимости, второй метод связан с. матричными уравнениями. Обсудим каждый из них.

Дерево достижимости представляет множество достижимости сети Петри. Рассмотрим, например, маркированную сеть Петри на рис. 7.8. Начальная маркировка её – (1, 0, 0). В этой начальной маркировке разрешены два перехода: t₁ и t₂. Поскольку мы хотим рассмотреть все множества достижимости, определим новые вершины в дереве достижимости для (достижимых) маркировок, получающихся в результате запуска каждого из этих двух переходов. Дуга, помеченная запускаемым переходом, приводит из начальной маркировки к каждой из новых маркировок (рис. 7.9). Это (частичное) дерево показывает все маркировки, непосредственно достижимые из начальной маркировки.

Рис.7.8.

Теперь необходимо рассмотреть все маркировки, достижимые из новых маркировок. Из маркировки (1, 1, 0) можно снова запустить t₁ (получая (1, 2, 0)) и t₂ (получая (0, 2, 1)); из (0, 1, 1) можно запустить t₃ (получая (0, 0, 1)). Это порождает дерево, изображённое на рис. 7.10. Начиная с трёх новых маркировок, необходимо повторить этот процесс, порождая новые маркировки, которые нужно ввести в дерево.

Рис. 7.9.

Заметим, что маркировка (0, 0, 1) пассивная; никакой переход в ней не является разрешённым, поэтому никакие новые маркировки из этой пассивной маркировки в дереве порождаться не будут. Кроме того, необходимо отметить, что маркировка (0, 1,1), порождаемая запуском t₃ в (0, 2, 1), была уже порождена непосредственно из начальной маркировки запуском t₂.

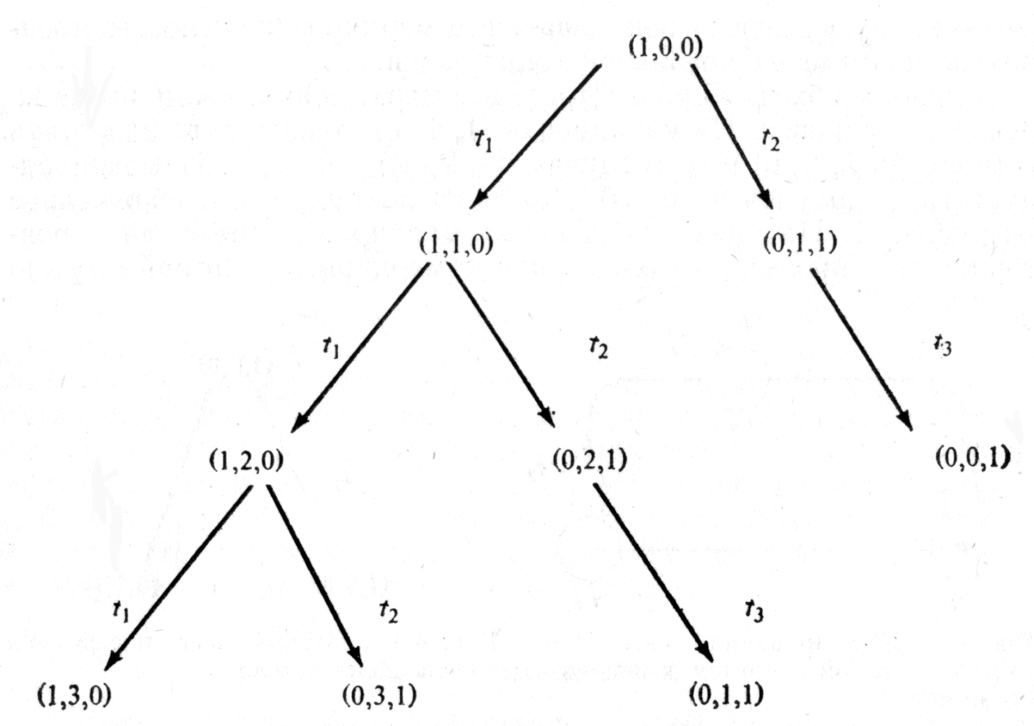Рис. 7.10.

Если эту процедуру повторять снова и снова, каждая достижимая маркировка окажется порождённой. Однако получившееся дерево достижимости может оказаться бесконечным. Будет порождена каждая маркировка из множества достижимости, поэтому для любой сети Петри с бесконечным множеством достижимости соответствующее дерево также должно быть бесконечным. Даже сеть Петри с конечным множеством достижимости может иметь бесконечное дерево (рис. 7.11).

Рис. 7.11. Простая сеть Петри с бесконечным деревом

Дерево представляет все возможные последовательности запусков переходов. Всякий путь в дереве, начинающийся в корне, соответствует допустимой последовательности переходов. Для превращения дерева в полезный инструмент анализа необходимо найти средства ограничения его до конечного размера.

Приведение к конечному представлению осуществляется несколькими способами. Нам необходимо найти те средства, которые ограничивают введение новых маркировок (называемых граничными вершинами) на каждом шаге. Здесь могут помочь пассивные маркировки – маркировки, в которых нет разрешённых переходов. Эти пассивные маркировки называются терминальными вершинами. Другой класс маркировок – это маркировки, ранее встречавшиеся в дереве. Такие дублирующие маркировки называются дублирующими вершинами; никакие последующие маркировки рассматривать нет нужды – все они будут порождены из места первого появления дублирующей маркировки в дереве.

В сети Петри на рис. 7.7, например, можно запустить переход t₁ столько раз, сколько необходимо для того, чтобы получить произвольное число фишек в p₂.

Представим бесконечное число маркировок, получающихся из циклов такого типа, с помощью специального символа w, который обозначает «бесконечность». Для любого постоянного a определим

Для построения дерева достижимости необходимы только эти операции над w.

Теперь можно точно сформулировать действительный алгоритм построения дерева достижимости. Каждая вершина i дерева связывается с расширенной маркировкой m [ i ]; в расширенной маркировке число фишек в позиции может быть либо неотрицательным целым, либо w. Каждая вершина классифицируется или как граничная вершина, терминальная вершина, дублирующая вершина, или как внутренняя вершина. Граничными являются вершины, которые ещё не обработаны алгоритмом; алгоритм превратит их в терминальные, дублирующие или внутренние вершины.

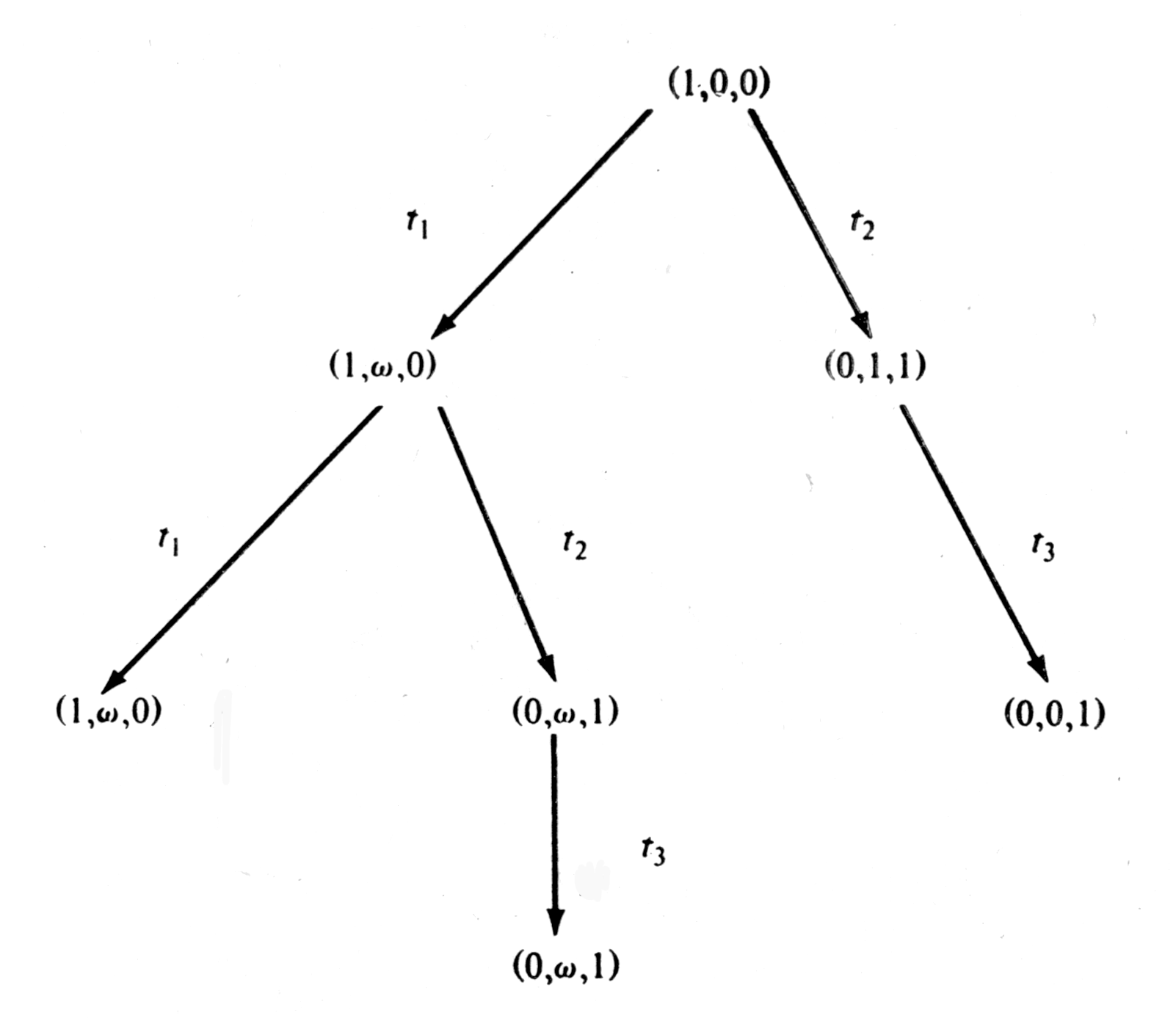
Рис. 7.12.

Алгоритм начинает работу с определения начальной маркировки корнем дерева, т.е. граничной вершиной. До тех пор пока имеются граничные вершины, они обрабатываются алгоритмом.

Пусть х – граничная вершина, которую необходимо обработать.

1. Если в дереве имеется другая вершина у, не являющаяся граничной, и с ней связана та же маркировка, m [ х ] = m [ y ], то вершина х – дублирующая.

2. Если для маркировки m[х] ни один из переходов не разрешён (т.е. d(m [ x ], t_j) не определено для всех t_j Î T), то х – терминальная вершина.

3. Для всякого перехода t_j Î T, разрешённого в m [ х ] (т.е. d(m [ х ], t_j) определено), создать новую вершину z дерева достижимости. Маркировка m [ z ], связанная с этой вершиной, определяется для каждой позиции p_i следующим образом:

а) Если .m [ x ] _i = w, то m [ z ] _i = w.

б) Если на пути от корневой вершины к х существует вершина у с m[y] < d(mlxl, t_j) и m[y]_i < d(m[x], t_j)_i, то m[z]_i = w.

в) В противном случае m[z]_i = d(m[х], t_j)_i.

Дуга, помеченная t_j, направлена от вершины х к вершине z. Вершина х переопределяется как внутренняя, вершина z становится граничной.

Когда все вершины дерева – терминальные, дублирующие или внутренние, алгоритм останавливается.

На рис. 7.12 представлено дерево достижимости для сети Петри на рис. 7.7.

Лекция 8

Дата добавления: 2014-12-16