Матричные уравнения

Второй подход к анализу сетей Петри основан на матричном представлении сетей Петри. Альтернативным по отношению к определению сети Петри в виде (Р, Т, I, O) является определение двух матриц D^- и D⁺, представляющих входную и выходную функции. Каждая матрица имеет m строк (по одной на переход) и n столбцов (по одному на позицию). Определим D^-[j, i] = #(p_i, I(t_j)), a D⁺[j, i] = #(p_i, O(t_j)). D^- определяет входы в переходы, D ⁺ – выходы.

Матричная форма определения сети Петри (Р, Т, D^-, D⁺) эквивалентна стандартной форме, используемой нами, но позволяет дать определения в терминах векторов и матриц. Пусть е[j] – m -вектор, содержащий нули везде, за исключением j -ой компоненты. Переход t_j представляется m -вектором e [ j ](здесь e [ j ] – вектор-строка).

Теперь переход t_j в маркировке m разрешён, если m ³ е[j], а результат запуска перехода t_j в маркировке m, записывается как

,

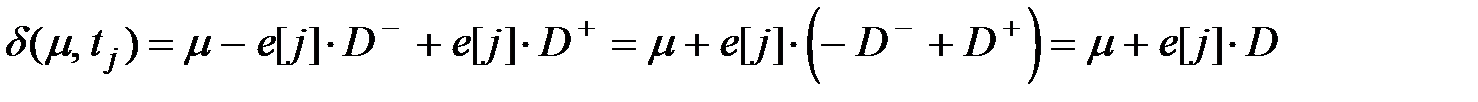где D = D⁺ – D⁺ – составная матрица изменений.

Тогда для последовательности запусков переходов 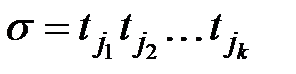имеем

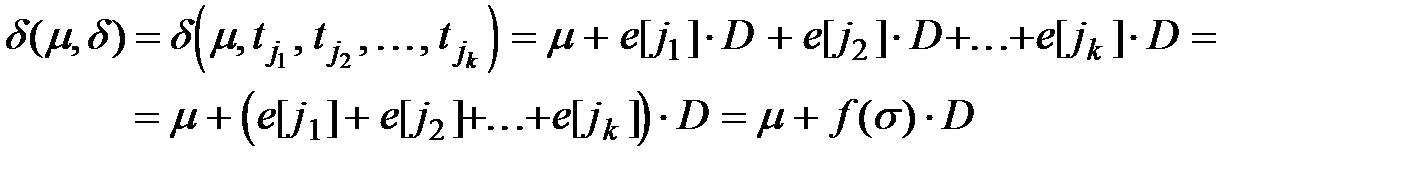
Вектор f(s) = e[j₁] + е[j₂] +... + e[j_k] называется вектором запусков последовательности . i –й элемент вектора f(s), f(s)_i – это число запусков перехода t_i в последовательности . Вектор запусков, следовательно, является вектором с неотрицательными целыми компонентами.

Для того чтобы показать полезность такого матричного подхода к сетям Петри, рассмотрим, например, задачу сохранения: является ли данная маркированная сеть Петри сохраняющей? Для того чтобы показать сохранение, необходимо найти (ненулевой) вектор взвешивания, для которого взвешенная сумма по всем достижимым маркировкам постоянна. Пусть w-n´1 – вектор-столбец. Тогда, если m – начальная маркировка, а m' – произвольная достижимая маркировка, необходимо, чтобы 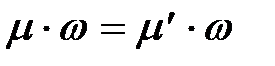. Теперь, поскольку m' достижима, существует последовательность запусков переходов s, которая переводит сеть из m в m'. Поэтому

.

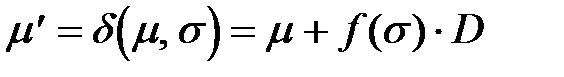Следовательно, , поэтому .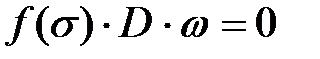

Поскольку это должно быть верно для всех f(s), имеем . Таким образом, сеть Петри является сохраняющей тогда и только тогда, когда существует такой положительный вектор w, что . Это обеспечивает простой алгоритм проверки сохранения, а также позволяет получать вектор взвешивания w.

Развитая матричная теория сетей Петри является инструментом для решения проблемы достижимости. Предположим, что маркировка m' достижима из маркировки m. Тогда существует последовательность (возможно, пустая) запусков переходов s, которая приводит из m к m'. Это означает, что f(s) является неотрицательным целым решением следующего матричного уравнения для х:

. (*)

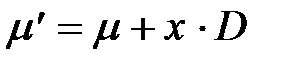Следовательно, если m' достижима из m тогда уравнение (*) имеет решение в неотрицательных целых; если уравнение (*) не имеет решения, тогда m' недостижима из m.

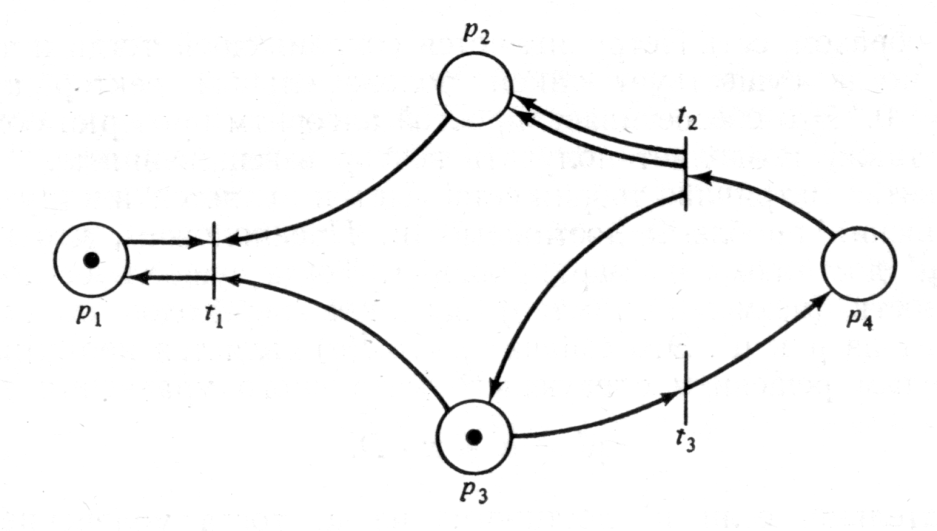Рис. 8.1.

Рассмотрим, например, маркированную сеть Петри на рис. 8.1. Матрицы D^- и D ⁺ имеют вид:

а матрица D:

В начальной маркировке m = (1, 0, 1, 0) переход t₃ разрешён и приводит к маркировке m', где

Последовательность 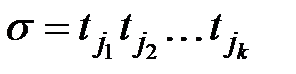представляется вектором запусков f(s)=(1, 2, 2) и получает маркировку m':

Для определения того, является ли маркировка (1,8,0, 1) достижимой из маркировки (1, 0, 1, 0), имеем уравнение

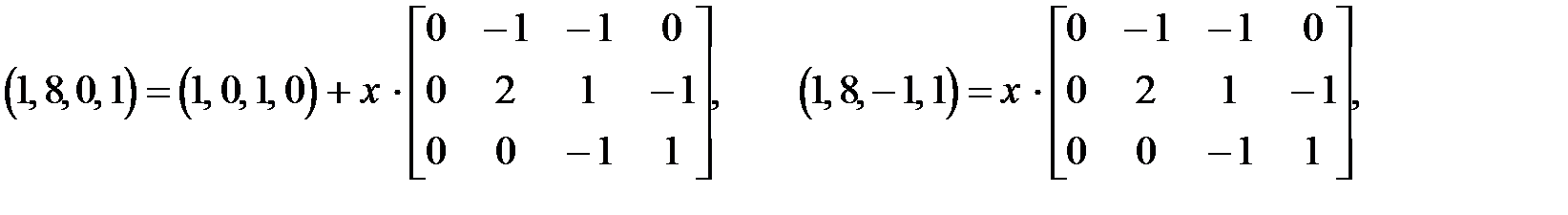
которое имеет решение x = (0, 4, 5). Это соответствует последовательности s = t₃t₂t₃t₂t₃t₂t₃t₂t₃.

Далее мы можем показать, что маркировка (1,7,0, 1) недостижима из маркировки (1, 0, 1, 0), поскольку матричное уравнение

не имеет решения.

Матричный подход к анализу сетей Петри очень перспективен, но имеет и некоторые трудности. Заметим, прежде всего, что матрица D сама по себе не полностью отражает структуру сети Петри. Переходы, имеющие как входы, так и выходы из одной позиции (петли), представляются соответствующими элементами матриц D^- и D ⁺, но затем взаимно уничтожаются в матрице D = D^- – D⁺. Это отражено в предыдущем примере позицией p₁ и переходом t₁.

Рис. 8.2.

Другая проблема – это отсутствие информации о последовательности в векторе запуска. Рассмотрим сеть Петри на рис. 8.2. Предположим, мы хотим определить, является ли маркировка (0, 0, 0, 0, 1) достижимой из (1, 0, 0, 0, 0).

Тогда имеем уравнение

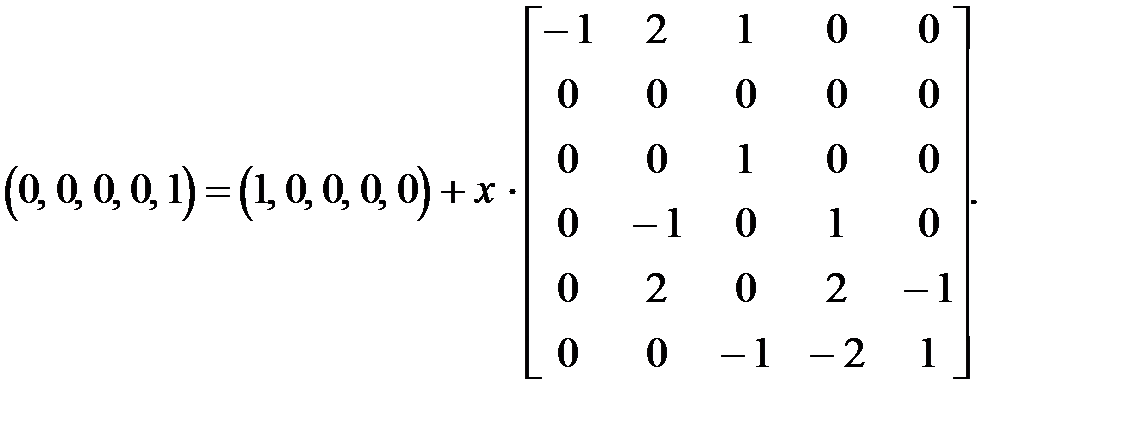
Это уравнение не имеет однозначного решения, но сводится к множеству решений {s½ f (s) = (1, x₂, x₆-1, 2x₆, x₆-1, x₆)}. Оно определяет взаимосвязь между запусками переходов. Если положим x₆=1 и x₂=1, то f (s) = (1, 1, 0, 2, 0, 1), но этому вектору запуска соответствуют как последовательность t₁t₂t₄t₄t₆, так и последовательность t₁t₄t₂t₄t₆. Следовательно, хотя и известно число запусков переходов, порядок их запуска неизвестен.

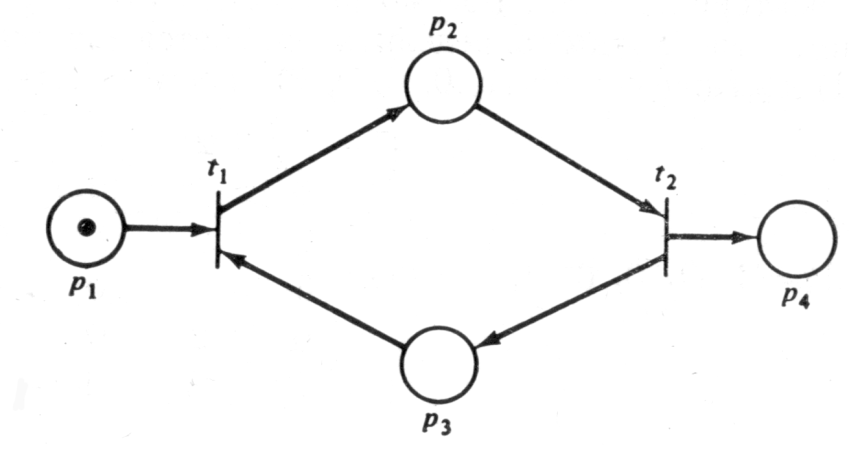Рис. 8.3.

Ещё одна трудность заключается в том, что решение уравнения (*) является необходимым для достижимости, но недостаточным. Рассмотрим простую сеть Петри, приведённую на рис. 8.3. Если мы хотим определить, является ли (0, 0, 0, 1) достижимым из (1,0,0,0), необходимо решить уравнение

Это уравнение имеет решение f (s) = (1, 1), соответствующее двум последовательностям: t₁t₂ и t₂t₁. Но ни одна из этих двух последовательностей переходов невозможна, поскольку в (1,0, 0, 0) ни t₁, ни t₂ не разрешены. Таким образом, решения уравнения (*) недостаточно для доказательства достижимости.

Возможность недействительных решений уравнения (*) (решений, которые не соответствуют возможным последовательностям переходов) стала причиной только ограниченного исследования матричного представления сетей Петри.

Дата добавления: 2014-12-16