
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Действия над комплексными числами в алгебраической форме
|
|
|
|
Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами.
Пример 2. Даны комплексные числа z 1 = 2 + 3 i, z 2 = 5 – 7 i. Найти:
а) z 1 + z 2; б) z 1 – z 2; в) z 1 z 2.
Решение.
а) z 1 + z 2 = (2 + 3 i) + (5 – 7 i) = 2 + 3 i + 5 – 7 i = (2 + 5) + (3 i – 7 i) = 7 – 4 i;
б) z 1 – z 2 = (2 + 3 i) – (5 – 7 i) = 2 + 3 i – 5 + 7 i = (2 – 5) + (3 i + 7 i) = – 3 + 10 i;
в) z 1 z 2 = (2 + 3 i)(5 – 7 i) = 10 – 17 i + 15 i – 21 i 2 = 10 – 14 i + 15 i + 21 = (10 + 21) + (– 14 i + 15 i) = 31 + i
(здесь учтено, что i 2 = – 1).
Пример 3. Выполнить деление:
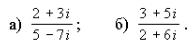
Решение.
а) Имеем
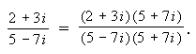
Произведем умножение для делимого и делителя в отдельности:
(2 + 3 i)(5 + 7 i) = 10 + 14 i + 15 i + 21 i 2 = – 11 + 29 i;
(5 – 7 i)(5 + 7 i) = 25 – 49 i 2 = 25 + 49 = 74.
Итак,
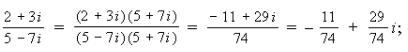
Пример 4. Решите уравнение:
x 2 – 6 x + 13 = 0
Решение. а) Найдем дискриминант по формуле
D = b 2 – 4 ac.
Так как a = 1, b = – 6, c = 13, то
D = (– 6)2 – 4*1*13 = 36 – 52 = – 16;
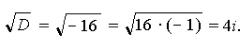
Корни уравнения находим по формулам
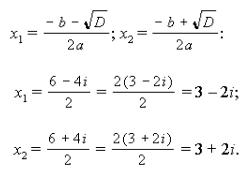
Текст задания
1–7. Вычислите:
1. i 66; i 143; i 216; i 137.
2. i 43 + i 48 + i 44 + i 45.
3. (i 36 + i 17) i 23.
4. (i 133 + i 115 + i 200 + i 142)(i 17 + i 36).
5. i 145 + i 147 + i 264 + i 345 + i 117.
6. (i 13 + i 14 + i 15) i 32.
7. (i 64 + i 17 + i 13 + i 82)(i 72 – i 34).
8–13. Найдите значения x и y из равенств:
8. 7 x + 5 i = 1 – 10 iy.
9. (2 x + y) – i = 5 + (y – x) i.
10. x + (3 x – y) i = 2 – i.
11. (1 + 2 i) x + (3 – 5 i) y = 1 – 3 i.
12. (2 – i) x + (1 + i) y = 5 – i.
13. (3 i – 1) x + (2 – 3 i) y = 2 – 3 i.
14–21. Произведите сложение и вычитание комплексных чисел:
14. (3 + 5 i) + (7 – 2 i).
15. (6 + 2 i) + (5 + 3 i).
16. (– 2 + 3 i) + (7 – 2 i).
17. (5 – 4 i) + (6 + 2 i).
18. (3 – 2 i) + (5 + i).
19. (4 + 2 i) + (– 3 + 2 i).
20. (– 5 + 2 i) + (5 + 2 i).
21. (– 3 – 5 i) + (7 – 2 i).
22–29. Произведите умножение комплексных чисел:
22. (2 + 3 i)(5 – 7 i).
23. (6 + 4 i)(5 + 2 i).
24. (3 – 2 i)(7 – i).
25. (– 2 + 3 i)(3 + 5 i).
26. (1 – i)(1 + i).
27. (3 + 2 i)(1 + i).
28. (6 + 4 i)*3 i.
29. (2 – 3i)(– 5i).
30–37. Выполните действия:
30. (3 + 5 i)2.
31. (2 – 7 i)2.
32. (6 + i)2.
33. (1 – 5 i)2.
34. (3 + 2 i)3.
35. (3 – 2 i)3.
36. (4 + 2 i)3.
37. (5 – i)3.
38–43. Выполните действия:
38. (3 + 2 i)(3 – 2 i).
39. (5 + i)(5 – i).
40. (1 – 3 i)(1 + 3 i).
41. (7 – 6 i)(7 + 6 i).
42. (a + bi)(a – bi).
43. (m – ni)(m + ni).
44–55. Выполните деление:

56–60. Выполните действия:

61 - 64. Решите уравнения:
61. x 2 – 4 x + 13 = 0.
62. x 2 + 3 x + 4 = 0.
63. 2,5 x 2 + x + 1 = 0.
64. 4 x 2 – 20 x + 26 = 0.
Практическая работа № 4
Тема: Корни и степени
Цель работы: закрепить знания и умения студентов по освоению применения формул при выполнении вычислений и решении иррациональных уравнений.
Теоритическое обоснование:
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 8159; Нарушение авторских прав?; Мы поможем в написании вашей работы!