Определение комплексного числа

Степени мнимой единицы

Понятие мнимой единицы

Допустим, что существует такое число, квадрат которого равен – 1. Обозначим это число буквой i; тогда можно записать: i ² = – 1.

Число i будем называть мнимой единицей (i – начальная буква французского слова imaginaire – «мнимый»), а предыдущее равенство будем считать определением мнимой единицы.

Из этого равенства находим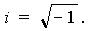

Введение мнимой единицы позволяет нам теперь извлекать корни квадратные из отрицательных чисел.

Например,

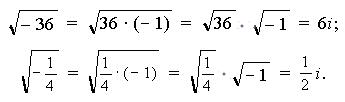
Рассмотрим степени мнимой единицы:

i;
i ² = – 1;
i ³ = i ² *i = (– 1) i = – i;
i ⁴ = i ^3* i = – i*i = – i ² = – (– 1) = 1;
i ⁵ = i ^4* i = 1* i = i;
i ⁶ = i ^5* i = i*i = i ² = – 1;
i ⁷ = i ^6* i = (– 1)* i = – i;
i ⁸ = i ^7* i = – i*i = 1;

Если выписать все значения степеней числа i, то мы получим такую последовательность: i, – 1, – i, 1, i, – 1, – i, 1 и т. д. Легко видеть, что значения степеней числа i повторяются с периодом, равным 4.

Так, i = i, i ² = – 1, i ³ = – i, i ⁴ = 1, i ⁵ = i, i ⁶ = – 1, i ⁷ = – i, i ⁸ = 1, i ⁹ = i, i ¹⁰ = – 1, i ¹¹ = – i, i ¹² = 1.

Мы знакомы с действительными числами и с мнимыми единицами. Рассмотрим теперь числа нового вида.

Определение 1. Числа вида a + bi, где a и b – действительные числа, i – мнимая единица, будем называть комплексными.

Число a будем назвать действительной частью комплексного числа, bi – мнимой частью комплексного числа, b – коэффициентом при мнимой части. Возможны случаи, когда действительные числа a и b могут быть равными нулю. Если a = 0, то комплексное число bi называется чисто мнимым. Если b = 0, то комплексное число a + bi равно a и называется действительным. Если a = 0 и b = 0 одновременно, то комплексное число 0 + 0 i равно нулю. Итак, мы получили, что действительные числа и чисто мнимые числа представляют собой частные случаи комплексного числа.

Запись комплексного числа в виде a + bi называется алгебраической формой комплексного числа.

Два комплексных числа a + bi и c + di условились считать равными тогда и только тогда, когда в отдельности равны их действительные части и коэффициенты при мнимой единице, т. е. a + bi = c + di, если a = c и b = d.

Пример 1. Найти x и y из равенства:

а) 3 y + 5 xi = 15 – 7 i;
б) (2 x + 3 y) + (x – y) i = 7 + 6 i.

Решение. а) Согласно условию равенства комплексных чисел имеем 3 y = 15, 5 x = – 7. Отсюда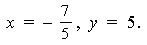

б) Из условия равенства комплексных чисел следует

Умножив второе уравнение на 3 и сложив результат с первым уравнением, имеем 5 x = 25, т. е. x = 5. Подставим это значение во второе уравнение: 5 – y = 6, откуда y = – 1. Итак, получаем ответ: x = 5, y = – 1.

Дата добавления: 2014-12-16