
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры решения показательных уравнений и неравенств
|
|
|
|
Показательные уравнения
Уравнение, которое содержит неизвестное в показателе степени, называется показательным уравнением.
Самое простое показательное уравнение имеет вид
| ax = b, где a > 0, a ≠ 1. |
Решить уравнение:
1) 1000x=100
Представим левую и правую часть уравнения в виде степени, имеющую одинаковые основания:
103x=102
Теперь, когда основания одинаковые, нужно приравнять показатели степеней.
3x=2
x=2/3
Ответ: x=2/3.
Главное в показательных уравнениях - свести левую и правую часть уравнения к общему основанию:
2) (2/5)x=(5/2)4
Представим (2/5)x как (5/2)-x:
(5/2)-x=(5/2)4
Основания одинаковые, следовательно, приравниваем показатели:
-x=4
x=-4
Ответ: x=-4
3) √3х=9
√3х распишем как 3x/2, а 9 - как 32:
3х/2=32
Приравниваем показатели:
х/2=2
х=4
Ответ: x=4
4) 3х2-х-2=81
Заметим, что 81=34
3х2-х-2=34
Приравниваем показатели:
х2-х-2=4
х2-х-6=0
Получили квадратное уравнение:
D=1+24=25, D>0, следовательно, уравнение имеет два действительных корня
х1=(1+5)/2=3
х2=(1-5)/2=-2
Ответ: х=3 и х=-2
5) 4х+1+4х=320
В таких случаях выносится основание с наименьшим показателем. В данном уравнении наименьшим показателем является х. Вынесем 4х за скобки:
4х(4+1)=320
4х*5=320
Представим 320 в виде 5*43, тогда:
4х*5=5*43
Поделим левую и правую часть уравнения на 5:
4х=43
Приравняем показатели:
х=3
Ответ: х=3
6) 7х+2+4*7х-1=347
Степенью с наименьшим показателем в этом уравнении является х-1, следовательно, за скобки выносим 7x-1. Получаем:
7х-1*(73+4)=347
7х-1*347=347
Поделим левую и правую часть уравнения на 347:
7х-1=1
Заметим, что любое число в нулевой степени равно 1. Следовательно, распишем 1 как 70:
7х-1=70
Приравняв показатели, получим:
х-1=0
х=1
Ответ: х=1
7) 4х-5*2х+4=0
Представим 4х как 22х, получим:
22х-5*2х+4=0
Введем подстановку: 2х обозначим переменной t. Cледовательно: 22х=t2. Получим:
t2-5t+4=0
Найдем корни уравнения по теореме Виета:
t1=1
t2=4
Заменим t на 2х:
2х=1
Заметим, что 20=1
2х=20
Приравняем показатели:
х=0
2х=4
Заметим, что 4=22
2х=22
Приравняем показатели:
х=2
Уравнение имеет два действительных корня 0 и 2.
Ответ: х=0 и х=2
Решить неравенство:
1) 45-2x<0,25.
Представим правую часть в виде: 0,25=(25/100)=(1/4)=4-1;
45-2x<4-1; функция у=4х с основанием 4>1 возрастает на R, поэтому, опуская основания степеней, знак неравенства сохраним:
5-2x<-1; — 2x<-1-5; — 2x<-6 |:(-2) при делении обеих частей неравенства на отрицательное число, знак неравенства меняют на противоположный: x>3.
 Ответ: (3; +∞).
Ответ: (3; +∞).
2) 0,42х+1≥0,16.
Представим число 0,16 в виде степени числа 0,4. Получаем: 0,42х+1 ≥ 0,42; основание степеней – число 0,4 — удовлетворяет условию: 0<0,4<1; поэтому, опускаем основания степеней, а знак неравенства меняем на противоположный:
2х+1 ≤ 2; 2х≤2-1; 2х≤1 |:2 x≤0,5.
 Ответ: (-∞; 0,5].
Ответ: (-∞; 0,5].
3) 23-x+21-x>40. Применим формулу: ax+y = ax∙ay. Запишем неравенство в виде:
23∙2-x+21∙2-x>40; Вынесем общий множитель за скобки:
2-x∙(23+21)>40; упрощаем левую часть:
2-x∙(8+2)>40;
2-x∙10>40 |:10
2-x>4;
2-x>22; основание степени — число 2>1, значит, знак неравенства сохраняем:
— x>2 |:(-1) при делении обеих частей неравенства на отрицательное число — знак неравенства меняют на противоположный: x<-2.
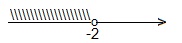 Ответ: (-∞; -2).
Ответ: (-∞; -2).
Текст задания
| Показательные уравнения и неравенства Вариант 1 | ||
| А) Выберите номер правильного ответа | ||
| А1 | Найдите сумму корней уравнения: 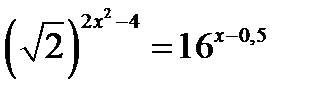
| 1)  2) 2) 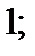 3) 3)  4) 4) 
|
| А2 | Если 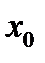 - корень уравнения - корень уравнения  , то значение выражения , то значение выражения  равно равно
| 1)  2) 2)  3) 3)  4) 4) 
|
| А3 | Найдите произведение корней уравнения 
| 1)-  2) 2) 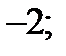 3) 3)  4) 4) 
|
| А4 | Найдите наименьшее целое решение неравенства 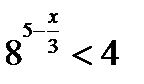
| 1)  2) 2)  3) 3) 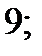 4) 4) 
|
| А5 | Найдите наибольшее целое решение неравенства 
| 1) 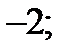 2) 2) 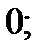 3) 3) 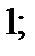 4) 4) 
|
| В) Напишите правильный ответ | ||
| В1 | Решите уравнение 
| |
| В2 | Решите неравенство:  
| |
| В3 | Если 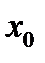 и и 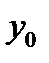 - решение системы уравнений - решение системы уравнений 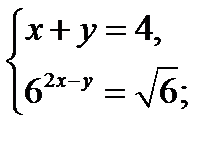 то значение выражения то значение выражения  равно равно
| |
| С) Приведите подробное решение данного задания. | ||
| С | При каких значениях параметра 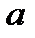 уравнение уравнение  имеет ровно один корень имеет ровно один корень
|
| Показательные уравнения и неравенства Вариант 2 | |||
| А) Выберите номер правильного ответа | |||
| А1 | Найдите сумму корней уравнения: 
| 1) 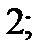 2) 2) 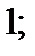 3) 3)  4) 4) 
| |
| А2 | Если 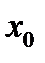 - корень уравнения - корень уравнения 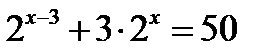 , то значение выражения , то значение выражения  равно равно
| 1) 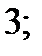 2) 2)  3) 3)  4) 4) 
| |
| А3 | Найдите произведение корней уравнения 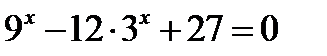
| 1)-  2) 2)  3) 3)  4) 4) 
| |
| А4 | Найдите наибольшее целое решение неравенства 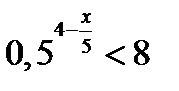
| 1)  2) 2)  3) 3)  4) 4) 
| |
| А5 | Найдите наименьшее целое решение неравенства 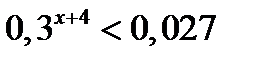
| 1)  2) 2) 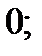 3) 3) 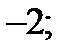 4) 4) 
| |
| В) Напишите правильный ответ | |||
| В1 | Решите уравнение 
| ||
| В2 | Решите неравенство:  
| ||
| В3 | Если 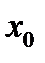 и и 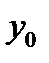 - решение системы уравнений - решение системы уравнений  то значение выражения то значение выражения 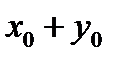 равно равно
| ||
| С) Приведите подробное решение данного задания. | |||
| С | При каких значениях параметра 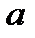 уравнение уравнение  имеет ровно один корень имеет ровно один корень
| ||
| Показательные уравнения и неравенства Вариант 3 | ||
| А) Выберите номер правильного ответа | ||
| А1 | Найдите сумму корней уравнения: 
| 1)  2) 2) 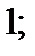 3) 3)  4) 4) 
|
| А2 | Если 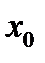 - корень уравнения - корень уравнения  , то значение выражения , то значение выражения 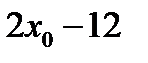 равно равно
| 1)  2) 2) 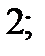 3) 3)  4) 4) 
|
| А3 | Найдите произведение корней уравнения 
| 1)  2) 2) 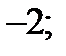 3) 3)  4) 4) 
|
| А4 | Найдите наименьшее целое решение неравенства 
| 1) 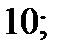 2) 2)  3) 3) 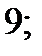 4) 4) 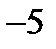
|
| А5 | Найдите наибольшее целое решение неравенства 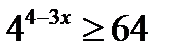
| 1) 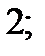 2) 2) 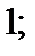 3) 3) 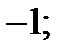 4) 4) 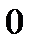
|
| В) Напишите правильный ответ | ||
| В1 | Решите уравнение 
| |
| В2 | Решите неравенство:  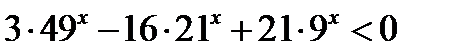
| |
| В3 | Если 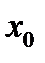 и и 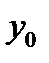 - решение системы уравнений - решение системы уравнений  то значение выражения то значение выражения  равно равно
| |
| С) Приведите подробное решение данного задания. | ||
| С | Найдите все значения  , при которых уравнение , при которых уравнение  имеет ровно два корня. имеет ровно два корня.
|
| Показательные уравнения и неравенства Вариант 4 | ||
| А) Выберите номер правильного ответа | ||
| А1 | Найдите сумму корней уравнения: 
| 1)  2) 2) 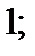 3) 3)  4) 4) 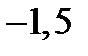
|
| А2 | Если 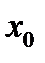 - корень уравнения - корень уравнения  , то значение выражения , то значение выражения  равно равно
| 1) 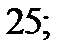 2) 2)  3) 3)  4) 4) 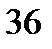
|
| А3 | Найдите произведение корней уравнения 
| 1)  2) 2)  3) 3) 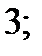 4) 4) 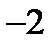
|
| А4 | Найдите наибольшее целое решение неравенства 
| 1) 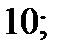 2) 2)  3) 3)  4) 4) 
|
| А5 | Найдите наименьшее целое решение неравенства 
| 1)  2) 2) 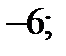 3) 3) 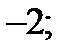 4) 4) 
|
| В) Напишите правильный ответ | ||
| В1 | Решите уравнение 
| |
| В2 | Решите неравенство:  
| |
| В3 | Если 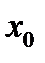 и и 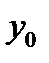 - решение системы уравнений - решение системы уравнений  то значение выражения то значение выражения  равно равно
| |
| С) Приведите подробное решение данного задания. | ||
| С | Найдите все значения  , при которых уравнение , при которых уравнение  имеет ровно один корень. имеет ровно один корень.
|
Практическая работа № 7
Тема: Логарифм числа. Логарифмическая функция и её свойства
Цель работы: закрепить знания и умения студентов по освоению логарифмов и свойств логарифмической функции.
Теоритическое обоснование:
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 9625; Нарушение авторских прав?; Мы поможем в написании вашей работы!