Геометрия

уметь:

- Распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями;

- Описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении;

- Анализировать в простейших случаях взаимное расположение объектов в пространстве;

- Изображать основные многогранники и круглые тела; выполнять чертежи по условиями задач;

- Строить простейшие сечения куба, призмы, пирамиды;

- Решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов);

- Использовать при решении стереометрических задач планиметрические факты и методы;

- Проводить доказательные рассуждения в ходе решения задач;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

- Исследования (моделирования) несложных практических ситуации на основе изученных форум и свойств фигур;

- Вычисления объемов и площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.

Практическая работа № 18

Тема: Параллельность прямых и плоскостей в пространстве

Цель работы: закрепить знания и умения студентов по освоению темы методом решения задач.

Теоритическое обоснование:

[2, стр. 239 – 247]

Текст задания:

Вариант 1

1. Дан треугольник МКР. Плоскость, параллельная прямой МК, пересекает МР в точке М₁, РК – в точке К_1. МК = 18 см, МР: М₁Р = 12: 5. Найти длину отрезка М₁К₁.

1. На сторонах АВ и АС треугольника АВС взяты соответственно точки Д и Е так, что ДЕ = 6 см и ВД: ДА = 4: 3. Плоскость α проходит через точки В и С параллельно отрезку ДЕ. Найти длину отрезка ВС.

1. Сторона АС треугольника АВС лежит в плоскости α. Через середину стороны АВ – точку М – проведена плоскость β, параллельная плоскости α и пересекающая сторону ВС в точке К. АС = 10 см. Найти длину отрезка МК.

1. Три прямые, проходящие через одну точку и не лежащие в одной плоскости, пересекают одну из плоскостей в точках А₁, В₁ и С₁, а другую – в точках А₂, В₂ и С₂. Причем А₁ – середина А₂М. Площадь треугольника А₁В₁С₁ равна 5 см². Найти площадь треугольника А₂В₂С₂.

Вариант 2

1. Дан треугольник ВСЕ. Плоскость, параллельная прямой СЕ, пересекает ВЕ в точке Е₁, ВС – в точке С₁. ВС = 28 см, С₁Е₁: СЕ = 3: 8. Найти длину отрезка ВС₁.

1. На сторонах АВ и АС треугольника АВС взяты соответственно точки Д и Е так, что ДЕ = 6 см и ВД: ДА = 2: 3. Плоскость α проходит через точки В и С параллельно отрезку ДЕ. Найти длину отрезка ВС.

1. Сторона АВ треугольника АВС лежит в плоскости α. Через середину стороны АС – точку Р – проведена плоскость β, параллельная плоскости α и пересекающая сторону ВС в точке Е. РЕ = 7 см. Найти длину отрезка АВ.

1. Три прямые, проходящие через одну точку и не лежащие в одной плоскости, пересекают одну из параллельных плоскостей в точках М₁, N₁ и К₁, а другую – в точках М₂, N₂ и К₂. Причем АМ₂ = 2АМ₁. Площадь треугольника М₂N₂К₂ = 10 см². Найти площадь треугольника М₁N₁К₁.

Контрольные вопросы:

[2, стр. 247]

Практическая работа № 19

Тема: Перпендикулярность прямых и плоскостей в пространстве. Геометрические преобразования в пространстве

Цель работы: закрепить знания и умения студентов по освоению темы методом решения задач.

Теоритическое обоснование:

[2, стр. 252 – 263]

Текст задания:

Вариант 1

1. Отрезок АВ перпендикулярен плоскости α, АС принадлежит плоскости α, СМ = МВ, АМ = 2,5см, АС = 3см. Найти длину отрезка АВ.

1. АВСД – квадрат и точка S не принадлежащая плоскости квадрата, АВ = √2см. Диагонали квадрата пересекаются в точке О. Отрезок SО перпендикулярен плоскости квадрата и равен √3см. Найти расстояние от точки S до вершин квадрата.

1. Отрезок АВ перпендикулярен плоскости α, наклонная АС равная 16см, проведена под углом в 30⁰ к плоскости α, а проекция ВД наклонной АД равна 6см. Найти длину наклонной АД.

1. Через сторону АД длиной 4см прямоугольника АВСД проведена плоскость α, составляющая со стороной АВ угол 30⁰. Расстояние от стороны ВС до плоскости α равно 1,5см. Найти диагональ прямоугольника.

1. В прямоугольном треугольнике АВС, угол С прямой, АВ = 5см, АС = √13см. Из точки Д опущен перпендикуляр ДВ на плоскость треугольника АВС, угол между наклонной ДС и её проекцией ВС равен 30⁰. Найти длину перпендикуляра ДВ.

Вариант 2

1. АВСД – параллелограмм, диагональ ВД принадлежит плоскости α, диагональ АС перпендикулярна плоскости α, сторона АВ равна 5см. Найти периметр параллелограмма.

1. Треугольник АВС – правильный, АВ = 3см, высоты АМ и СК пересекаются в точке О. Из точки Д не принадлежащей плоскости АВС опущен перпендикуляр ДО равный 1см. Найти расстояние от точки Д до вершин треугольника.

1. Отрезок АВ перпендикулярен плоскости α, наклонная АС равная 6√2см, проведена под углом в 45⁰ к плоскости α, а проекция ВД наклонной АД равна 8см. Найти длину наклонной АД.

1. Через сторону АД квадрата АВСД проведена плоскость α, составляющая с его диагональю АС угол 30⁰. Площадь квадрата равна 32см². Найти расстояние от стороны ВС до плоскости α.

1. В прямоугольном треугольнике АВС, угол С прямой, АВ = 15см, ВС = 9см. Из точки Д опущен перпендикуляр ДА на плоскость треугольника АВС равный 5см. Найти расстояние от точки Д до прямой ВС.

Контрольные вопросы:

[2, стр. 263]

Практическая работа № 20

Тема: Призма.

Цель работы: закрепить знания и умения студентов по освоению темы методом решения задач.

Теоритическое обоснование:

[2, стр. 297 – 300, 343]

Текст задания:

1. Вычислить поверхность и объем прямой призмы, у которой основание правильный треугольник, вписанный в круг радиуса r =2 метрам, а высота равна стороне правильного 6-угольника, описанного около того же круга.

2. Определить поверхность и объем правильной 8- угольной призмы, у которой высота 6 м, а сторона основания а = 8см.

3. Площадь основания прямой треугольной призмы равна 4√6 дм². Найдите площадь сечения призмы, проведённого через сторону одного основания и параллельную ей среднюю линию другого основания, если известно, что сечение образует с плоскостью основания угол 30⁰.

4. Основанием призмы служит ромб со стороной 2 см и острым углом 30⁰. Найдите объём призмы, если её высота равна 3 см.

5. Площадь основания прямой треугольной призмы равна 4√6 дм². Найдите площадь сечения призмы, проведённого через сторону одного основания и параллельную ей среднюю линию другого основания, если известно, что сечение образует с плоскостью основания угол 45⁰.

6. Найдите объём наклонной треугольной призмы, основанием которой служит равносторонний треугольник со стороной 2 см, если боковое ребро призмы равно стороне основания и наклонено к плоскости основания под углом 60⁰.

Контрольные вопросы:

[2, стр. 311(9 – 18), 349(4,5)]

Практическая работа № 21

Тема: Параллелепипед

Цель работы: закрепить знания и умения студентов по освоению темы методом решения задач.

Теоритическое обоснование:

[2, стр. 301 – 304, 340,341]

Текст задания:

1. Полная поверхность прямоугольного параллелепипеда 1714 м², а неравные стороны основания равны 25м и 14 м. Вычислить боковую поверхность и боковое ребро.

2. В прямоугольном параллелепипеде с квадратным основанием и высотой р проведена секущая плоскость через два противоположных боковых ребра. Вычислить полную поверхность параллелепипеда, зная, что площадь сечения равна S.

3. Основанием прямого параллелепипеда служит ромб со стороной 4 см и углом 60⁰ . Большая диагональ параллелепипеда образует с плоскостью основания угол 45⁰ . Найдите площадь боковой поверхности параллелепипеда.

4. В прямом параллелепипеде стороны основания 3 см и 4 см образуют угол 60⁰. Меньшая диагональ параллелепипеда образует с основанием угол 45⁰. Найдите площадь боковой поверхности параллелепипеда.

Контрольные вопросы:

[2, стр. 311(19 – 26), 349(2,3)]

Практическая работа № 22

Тема: Пирамида

Цель работы: закрепить знания и умения студентов по освоению темы методом решения задач.

Теоритическое обоснование:

[2, стр. 305 – 308, 346,347]

Текст задания:

1. Высота правильной четырехугольной пирамиды равна 8 см, сторона её основания – 12см. Вычислите длину бокового ребра пирамиды.

2. Сторона основания правильной треугольной пирамиды равна 5 см, боковое ребро образует с основанием 45⁰. Найдите объём пирамиды.

3.Высота правильной треугольной пирамиды равна 6 см, сторона её основания – 12см. Вычислите длину бокового ребра пирамиды.

4. Основанием четырехугольной пирамиды служит ромб со стороной 3 см и острым углом 45⁰. Найдите объём пирамиды, если её высота равна √2 см.

5. Определить боковую поверхность и объем правильной шестиугольной пирамиды, у которой высота равна 1 м, а апофема составляет с высотой угол 30⁰.

Контрольные вопросы:

[2, стр. 311(27 – 35), 349(6 – 8)]

Практическая работа № 23

Тема: Цилиндр

Цель работы: закрепить знания и умения студентов по освоению темы методом решения задач.

Теоритическое обоснование:

[2, стр. 319 – 321, 353,358]

Текст задания:

1. Длина окружности основания равностороннего цилиндра равна 16π см. Найдите диагональ осевого сечения цилиндра.

2. Диагональ осевого сечения равностороннего цилиндра равна 8√2. Найдите длину окружности.

3. Объем цилиндра, у которого высота вдвое больше диаметра, равен 1м³.Вычислить его высоту.

4. Диаметр основания цилиндра = 16 см, а его полная поверхность содержит 1546 см² Вычислить высоту этого цилиндра.

5. Найти вес железной цилиндрической трубки, внутренний диаметр которой 17см, внешний диаметр 18см, а длина 74 см. Удельный вес железа 7,7.

6. В сосуд, имеющий форму конуса, обращенного вершиной вниз, вливают 345г ртути. Зная, что угол при вершине конуса равен 60 ⁰, а уд вес ртути 13,596, вычислить высоту, до которой налита в сосуд ртуть.

Контрольные вопросы:

[2, стр. 333(1 – 5), 360(1,7)]

Практическая работа № 24

Тема: Конус

Цель работы: закрепить знания и умения студентов по освоению темы методом решения задач.

Теоритическое обоснование:

[2, стр. 322 – 325, 354,358]

Текст задания:

1. Образующая конуса равна 4 см. найдите площадь сечения, проведенного через две образующие, угол между которыми составляет 45⁰.

2. Образующая конуса равна 6 см. Найдите площадь сечения, проведённого через две образующие, угол между которыми составляет 60⁰.

3. Вычислить боковую поверхность и объем усеченного конуса, у которого радиусы оснований 27 и 18 см, а образующая 21 см.

4. Найти объем тела, происходящего от вращения правильного 6-ти угольника со стороной a вокруг одной из своих сторон.

5. Вычислить объем тела, происходящего от вращения правильного треугольника со стороной a вокруг оси, проходящей через его вершину и параллельной противоположной стороне.

6. Дан равносторонний DABС со стороной a. На BC строят квадрат BCDE, располагая его в противоположную сторону от треугольника. Вычислить объем тела, происходящего от вращения 5 - угольника ABEDС вокруг стороны AB.

Контрольные вопросы:

[2, стр. 333(6 – 11), 360(2,8)]

Практическая работа № 25

Тема: Шар

Цель работы: закрепить знания и умения студентов по освоению темы методом решения задач.

Теоритическое обоснование:

[2, стр. 326 – 331, 356,357,359]

Текст задания:

1. Сечение шара плоскостью имеет площадь 36π см². Чему равен радиус шара, если сечение удалено от его центра на расстояние 8 см.

2. Шар с центром в точке О касается плоскости в точке А. Точка В лежит в плоскости касания. Найдите объём и площадь поверхности шара, если АВ = 21 см, ВО = 29 см.

3. Линия пересечения сферы с плоскостью имеет длину 18π см. Чему равно расстояние от центра сферы до этой плоскости, если радиус сферы равен 15 см.

4. Шар пересечён плоскостью на расстоянии 8 см от центра. Площадь сечения 225π см². Найдите объём и площадь поверхности шара.

5. Прямоугольная трапеция с основаниями 5 см и 8 см и высотой 4 см вращается около большего основания. Определите объём и площадь поверхности тела вращения.

6. Прямоугольная трапеция с основаниями 10 см и 14 см и высотой 3 см вращается около меньшего основания. Определите объём и площадь поверхности тела вращения.

Контрольные вопросы:

[2, стр. 333(12 – 21), 360(4 – 6, 9)]

Практическая работа № 26

Тема: Декартовая система координат

Цель работы: закрепить знания и умения студентов по освоению темы методом решения задач.

Теоритическое обоснование:

[2, стр. 270 – 283]

Текст задания:

1. Найти уравнение прямой, проходящей через две точки: (-1, 2) и (2, 1).

2. Стороны треугольника заданы уравнениями: (AB) 2 x + 4 y + 1 = 0, (AC) x - y + 2 = 0, (BC) 3 x + 4 y -12 = 0. Найти координаты вершин треугольника.

3. Найти уравнение прямой, проходящей через точку A (2, 5) параллельно прямой 3 x - 4 y + 15 = 0.

4. Найти уравнение прямой, проходящей через точку A (5, -1) перпендикулярно к прямой 3 x - 7 y + 14 = 0.

5. Даны две противоположные вершины квадрата A (2, 1) и C (4, 5). Найти две другие.

6. Найти угол между двумя прямыми y = 2 x + 4 и y = 3 x - 1.

7. Найти угол между двумя прямыми 3 x + 4 y - 7 = 0 и 4 x - 3 y + 8 = 0.

8. Найти уравнения прямых, проходящих через точку A (3, 4) под углом в 60 градусов к прямой 2 x + 3 y + 6 = 0.

9. Через центр тяжести треугольника, вершины которого A (2, 3), B (-1, 4), C (5, 5), провести прямую, перпендикулярную стороне AB.

Контрольные вопросы:

[2, стр. 286(1 – 10, 14 – 16)]

Практическая работа № 27

Тема: Вектор. Координаты вектора в декартовой системе координат

Цель работы: закрепить знания и умения студентов по освоению темы методом решения задач.

Теоритическое обоснование:

[2, стр. 285]

Текст задания:

1. Найти равнодействующую двух сил 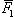и 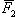, модули которых равны F ₁ = 5, F ₂ = 7, угол между ними θ = 60^°. Определить также углы α и β, образуемые равнодействующей с силам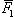и и .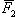

2. При каких значениях α и β вектор перпендикулярен вектору 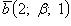, если ?

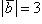3. Векторы 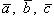лежат в одной плоскости и образуют попарно друг с другом углы 2 π /3. Разложить вектор 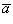по векторам и , если .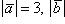

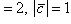4. Определить координаты точки C - середины вектора 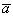по известным радиусам-векторам его концов A и B.

5. Даны два вектора: 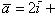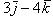и 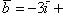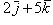. Найти проекции на координатные оси суммы и разности этих векторов.

6. Дан треугольник ABC. Прямая l пересекает прямые BC, CA, AB в точках A ₁, B ₁, C ₁. Доказать, что векторы 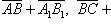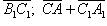коллинеарны.

7. Вектор 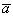задан координатами своих концов A и B: A (2, 1, -4); B (1, 3, 2). Найти проекции вектора 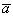на координатные оси и его направляющие косинусы.

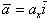
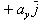
8. Найти проекцию вектора 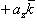на ось L, которая составляет с координатными осями углы λ, μ и ν.

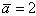
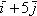
9. Дан вектор 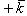. Найти его проекцию a_L на ось L, составляющую с координатными осями равные острые углы.

10. Два вектора 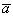и определены своими проекциями 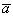{7, 2, -1} и {1, 2, -3}. Найти скалярное произведение этих векторов и угол между ними.

11. Определить угол между векторам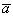и и , заданными своими проекциями 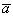{2, 1, -2}, {1, -4, 2}.

12. Найти площадь параллелограмма, построенного на векторах .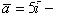

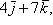
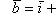
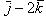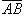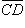13. Векторы и определены координатами своих концов: A (2, 4, 5); B (-1, -3, -2); C (4, 1, 7); D (-2, 3, 10). Найти: 1) векторное произведение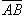 ; 2) его модуль; 3) направляющие косинусы векторного произведения.

14. Найти площадь треугольника, координаты вершин которого известны: A (-2, 1, 2); B (3, -3, 4); C (1, 0, 9).

15. Дана сила 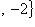и точка ее приложения A (2, -1, 3). Найти момент силы относительно начала координат и углы, составляемые им с координатными осями.

16. Найти объем пирамиды, если координаты ее вершин A ₁(x ₁, y ₁, z ₁); A ₂(x ₂, y ₂, z ₂); A ₃(x ₃, y ₃, z ₃); A ₄(x ₄, y ₄, z ₄).

17. Даны координаты вершин пирамиды A ₁(5, 1, -4), A ₂(1, 2, -1), A ₃(3, 3, -4) и A ₄(2, 2, 2). Определить ее объем.

Контрольные вопросы:

[2, стр. 286(18 – 20)]

Дата добавления: 2014-12-16