I. Основные понятия и формулы

Теоретические сведения

Теория вероятностей – раздел математики, в котором выясняются закономерности, возникшие при взаимодействии большого числа факторов или событий.

Событие – это всякий результат или исход опыта.

Случайное событие – это событие, которое может при осуществлении данных условий как произойти, так и не произойти и для которого имеется определённая вероятность его появления.

Относительная частота события P*(А) в серии опытов определяется отношением числа m появлений этого события к общему числу n проведённых измерений:

P*(А) (1)

Вероятность – числовая характеристика, степень возможности появления какого-либо случайного события при тех или иных условиях.

Статическая вероятность события (закон больших чисел) это предел, к которому стремится частота события при неограниченном увеличении числа испытаний:

P (A) = 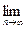; при этом 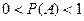(2)

Несовместимые события – это события, которые не могут произойти одновременно.

Событие невозможно, если P(A) = 0.

Событие достоверное, если P(A) = 1, т.е. в результате эксперимента оно должно произойти обязательно.

Дискретная случайная величина – это случайная величина, принимающая только определённые числовые значения.

Условие нормировки для дискретной случайной величины, имеющей n значений:

.

Непрерывная величина – величина, принимающая любые значения в данном интервале.

Простой статистический ряд – совокупность всех значений случайной величины, записанных в порядке их получения.

Выборка (выборочная совокупность) – часть значений 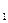(x , x ,…x ) случайной величины, отобранных для исследования из общей совокупности всех её значений.

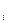Математическое ожидание дискретной случайной величины X есть сумма произведений всех её возможных значений x на их вероятности P : (3)

Для эмпирических распределений статистическим аналогомматематического ожидания является среднее арифметическое значение .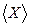

Математическим ожиданиемнепрерывной случайной величины X служит интервал:

M (X) = 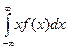(4),

где f(x) – плотность вероятности (функция распределения вероятностей).

Дисперсия D(Х) дискретной случайной величины X характеризует отклонение (рассеяние) этой случайной величины от её среднего значения (математического ожидания) и для опытных данных определяется формулой:

D(Х) = (5)

Среднее квадратичное отклонение < > - корень квадратный из дисперсии:

< > = (6)

Закон распределения случайной величины – это совокупность всех возможных значений X 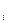случайной величины и соответствующих им вероятностей P .

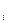Нормальный закон распределения случайных величин (закон Гаусса).

(7),

где <x> - математическое ожидание (среднее значение) случайной величины <x> = M (X);

- среднее квадратичное отклонение;

- основание натурального логарифма (неперово число);

f (x) – плотность вероятности (функция распределения вероятностей).

Распределение Больцмана:

n = n exp (-mgh/кТ) (8),

где n – концентрация молекул воздуха, находящихся в гравитационном поле Земли на высоте h;

n - концентрация молекул на высоте h = 0;

Т – температура;

m – масса молекулы;

к – постоянная Больцмана;

g – ускорение свободного падения.

Закон распределения молекул в газах по скоростям называется распределением Максвелла.

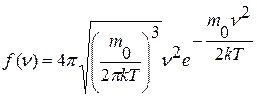(9),

где m_о – масса молекулы, k – постоянная Больцмана, Т – абсолютная температура газа, - скорость молекулы.

Гистограмма (от греч. histos – столб, gramma – черта, столбчатая диаграмма)- один из способов графического изображения статистических распределений какой-либо величины; представляет собой совокупность смежных прямоугольников, построенных на одной прямой.

Доверительный интервал – интервал, в который с определенной (доверительной) вероятностью попадает истинное значение измеряемой или исследуемой величины.

Доверительной вероятностью (надёжностью) результата серии измерений называется вероятность того, что истинное (действительное) значение измеряемой величины попадает в данный доверительный интервал.

Среднее арифметическое значение n измерений величины X:

<X> = 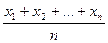= (10)

Абсолютная погрешность отдельного измерения:

= (i = 1,2,…n)

Средняя абсолютная погрешность опыта для измерений:

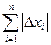< X> = = (11)

Относительная погрешность опыта:

Е = (12)

II. Основы теории ошибок и методы её практического применения для обработки экспериментальных данных

Все физические явления и свойства характеризуются различными физическими величинами. Для науки и техники большое значения имеют количественные характеристики, полученные в процессе измерения. Измерить физическую величину - это значит найти опытным путём её значение с помощью специальных технических средства. В результате измерения данная физическая величина сравнивается с её значением (эталоном), условно принятым за единицу.

Все измерения делятся на прямые (или непосредственные) и косвенные.

Прямым измерением называется такое измерение, при котором значение измеряемой величины получают путем непосредственного сравнения с её мерой или с помощью соответствующего прибора.

Этим способом измеряют сравнительно небольшое число физических величин (измерение длины линейкой, время - секундомером, напряжение - вольтметром, температуру - термометром и др.).

Косвенным измерением называется такое измерение, при котором значение искомой величины рассчитывают по формуле с помощью известной зависимости между искомой величиной и величинами, определяемыми путем прямых измерений. Например, определение объема тела по прямым измерениям его геометрических размеров, определение удельного сопротивления цилиндрического проводника прямыми измерениями длины, диаметра поперечного сечения и электрического сопротивления проводника и др.

Различают истинное и действительное значение физической величины. Под истинным значением физической величины понимают ее значение, которое абсолютно верно отражало бы эту величину. Проводя измерения физической величины, мы никогда не можем получить абсолютно точно истинное ее значение.

Действительным значением физической величины называется ее значение, найденное экспериментальным путем и настолько близкое к истинному значению, что для поставленной измерительной задачи может его заменить. Действительным значением измеряемой величины считают ее значение, полученное с помощью образцового прибора.

При измерении физических величин под действием самых разнообразных причин возникают погрешности измерений, т.е. отклонения результатов измерений от действительных значений искомых величин.

Погрешности, допускаемые при измерениях, принято делить на три типа: систематические, случайные и промахи (грубые ошибки).

Систематической погрешностью называют такую погрешность, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины одним и тем же методом и с помощью одних и тех же измерительных приборов.

Систематические погрешности появляются вследствие неисправности приборов (например, отклонение стрелки вольтметра или амперметра от нулевого деления при отсутствии тока), неточности метода исследований, каких - либо упущений экспериментатора, использование для вычислений неточных формул и т.д.

Систематические погрешности можно обнаружить только при внимательном и критическом отношении к состоянию и работе измерительных приборов, условиям измерения и получаемым результатам. Таким образом, систематические погрешности могут быть устранены или учтены.

Случайной погрешностью называется погрешность, которая обусловлена действием не поддающихся контролю многочисленных факторов, влияние которых невозможно учесть. Такие погрешности отличаются друг от друга в отдельных измерениях и носят случайную непредсказуемую величину. Методы определения случайных погрешностей рассматриваются в теории погрешностей, основанной на математической статистике и теории вероятностей, позволяющей по данным измерений вычислить наиболее вероятное значение измеряемой величины и оценить погрешность измерений.

Промах (грубая ошибка) - это такая погрешность измерения, которая оказывается значительно больше ожидаемых при данных условиях. Промах может возникнуть при небрежном выполнении измерений, неверно записанных показаний приборов, явном несоблюдении условий эксплуатации приборов и т.д. Промах можно интуитивно обнаружить, сравнивая числовые значения полученных результатов или их абсолютных погрешностей. Промахи должны быть исключены из результатов измерений.

Дата добавления: 2014-12-16