III. Расчет погрешности прямых измерений и доверительного интервала методом, основанным на определении средней квадратичной погрешности

Пусть величина 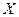непосредственно измерена n раз, при этом получены результаты 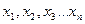. Результаты каждого измерения заносят в таблицу. Явно ошибочные результаты (промахи) отбрасывают.

1. Вычисляют среднее арифметическое значение измеряемой величины:

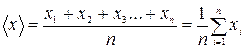(если n<30) (27) 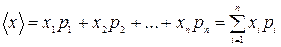(если n>30) (28)

2. Находят абсолютные погрешности отдельных измерений:

..........

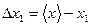
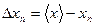(29)

3. Вычисляют квадраты абсолютных погрешностей отдельных измерений:

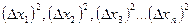
4. Определяют дисперсию (отклонение случайной величины от её среднего значения) по формуле (если ):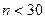

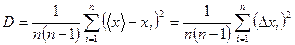(30)

5. Определяют среднюю квадратичную погрешность результата серии измерений:

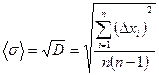(31)

6. По заданной доверительной вероятности (надежности) и числу проведенных измерений из таблицы находят соответствующее значение коэффициента Стьюдента .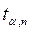

7. Вычисляют абсолютную погрешность всех измерений 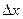и, следовательно, границы доверительного интервала (полуширину доверительного интервала):

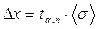(32)

8. Сравнивают полученное значение абсолютной погрешности 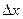с абсолютной погрешностью измерительного прибора :

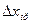а) если при сравнении окажется, что 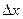гораздо меньше 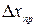, то за абсолютную погрешность результата берется абсолютная погрешность прибора 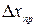, которая и определяет границы доверительного интервала, т.е.

;

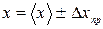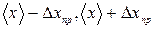
б) если окажется, что 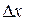гораздо больше 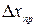, то величиной 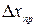пренебрегают и записывают окончательный результат в виде

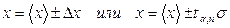(34)

Внимание. За абсолютную погрешность простых измерительных приборов (линейки, мензурки, секундомера и т.п.) принимают половину цены наименьшего деления шкалы прибора.

Абсолютную погрешность электроизмерительных приборов (и многих других) определяют по классу точности.

в) если окажется, что величина абсолютной погрешности результата 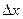сравнима с величиной абсолютной погрешности прибора 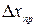, то значение абсолютной погрешности результата измерения нужно уточнить по следующей формуле:

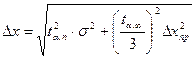(35),

где 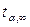- значение коэффициента Стьюдента, соответствующее выбранной надежности 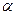и бесконечно большому числу измерений (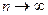). На практике значение коэффициента Стьюдента 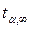берут из таблицы при 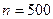. Окончательный результат записывают в форме:

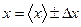(36).

9. Вычисляют относительную погрешность Е результата измерений:

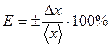(37)

Пример. При измерении температуры тела в однородных группах обследуемых получена следующая выборка: 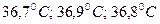. Сделать интервальную оценку среднего значения температуры при доверительной вероятности 0,95.

1. Находим среднее арифметическое значение температуры (по формуле 27):

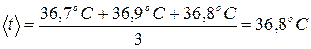
2. Находим абсолютную погрешность отдельного измерения:

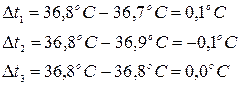
3. Вычисляем квадраты абсолютных погрешностей отдельных измерений: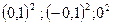

4. Вычисляем дисперсию по формуле 30

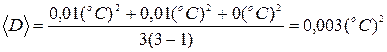
5. Средняя квадратичная погрешность результата измерения (формула 31) равна: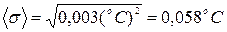

6. Для доверительной вероятност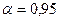и при 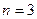коэффициент Стьюдента (из таблицы) равен: .

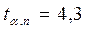7. Абсолютная погрешность 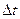результата измерений (полуширина доверительного интервала – формула 32) равна:

.

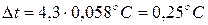8. Сравниваем полученное значение абсолютной погрешности с абсолютной погрешностью медицинского термометра, которая равна половине цены деления, т.е. ∆t_терм = 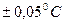. Следовательно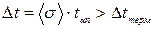

9. Пренебрегаем абсолютной погрешностью медицинского термометра и записываем окончательный результат (формула 36): .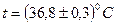

Примечание: Из правил округления в теории погрешностей имеется существенное исключение: при округлении погрешностей последняя цифра увеличивается на единицу, если старшая отбрасываемая цифра 3 или больше трех. В нашем случае .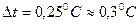

10. Вычисляем относительную погрешность Е (формула 37) результата измерения температуры тела:

.

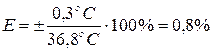IV. Расчет погрешностей косвенных измерений.

Пусть определяемая величина N является функцией нескольких переменных x, y, z величин, измеряемых непосредственно (прямые измерения), то есть N=f(x, y, z). Заметим, что в частном случае косвенно измеренная величина может выражаться только через одну прямую измеренную величину (например, объем шара V= 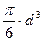(38), где d – диаметр шара).

1. Находят среднее арифметическое значение прямых измерений каждой величины x, y, z.

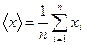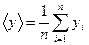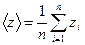; ; (39).

2. Вычисляют среднее арифметическое значение искомой величины: 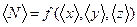(40).

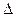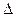3. Вычисляют абсолютные погрешности отдельных измерений всех величин x_i, y_i, 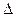z_i и их квадраты ( 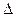x_i)², ( 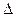y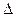_i)², ( z_i)².

4. Определяют дисперсию каждой измеренной величины:

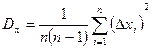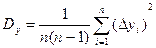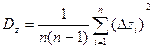; ; (41).

5. Рассчитывают средние квадратичные погрешности всех величин x, y, z: 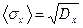; ; 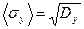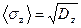(42).

6. Вычисляют среднюю квадратичную погрешность искомой величины по формуле:

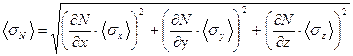(43),

где частные производные 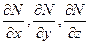рассчитывают при 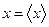, , 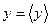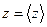. При получении выражения для любой частной производной остальные аргументы функции 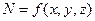считают постоянными.

7. Находят полуширину доверительного интервала искомой величины 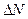, определив из таблицы значение коэффициента Стьюдента для заданной вероятности 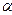и данного числа измерений (для всех измеряемых величин необходимо задавать одно и то же значение доверительной вероятности): 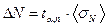(44).

8. Окончательный результат записывают в виде:

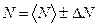(45).

Данная запись означает, что с доверительной вероятностью 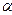значение искомой величины N попадает в интервал ().

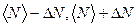9. Определяют относительную погрешность косвенного измерения величины N: 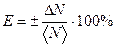(46).

Пример. Пусть при определении объёма V цилиндра в результате пяти измерений с помощью штангенциркуля высоты h цилиндра и диаметра d основания были получены результаты, которые занесены в таблицу:

№ п/п
h, мм	12,2	12,8	12,4	12,2	12,6
d, мм	5,0	4,7	5,2	4,9	4,8

Выполнить математическую обработку результатов измерений.

Доверительную вероятность считать равной 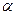=0,95.

Проведем выполнение математической обработки.

1. Найдем средние арифметические значения высоты и диаметра

(формула 39): ; .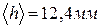

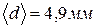2. Найдем среднее арифметическое значение объёма цилиндра:

;

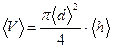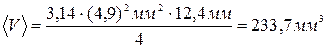
3. Вычислим абсолютные погрешности результатов измерения высоты цилиндра и его диаметра:

Δ h₁= 0,2мм; Δ d₁= -0,1мм;

Δ h₂= -0,4мм; Δ d₂= 0,2мм;

Δ h₃= 0; Δ d₃= -0,3мм;

Δ h₄= 0,2мм; Δ d₄= 0;

Δ h₅= -0,2мм; Δ d₅= 0,1мм.

4. Вычисляем дисперсию высоты D_h и диаметра D_d (формула 41):

;

;

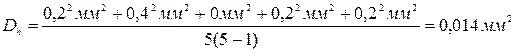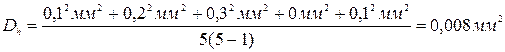5. Вычисляем средние квадратичные погрешности высоты 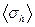и диаметра : = ;

= .

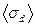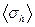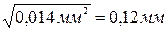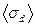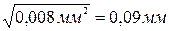6. Рассчитываем среднюю квадратичную погрешность объёма цилиндра V (формула 43):

; ; ;

;

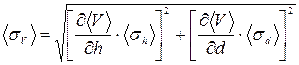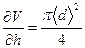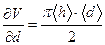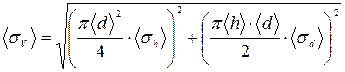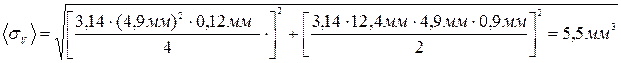
7. По таблице для α=0,95 и n =5находим значение коэффициента Стьюдента: .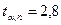

8. Вычисляем полуширину доверительного интервала ΔV:

ΔV= 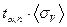; ΔV=2,8·5,5мм³ =15,4 мм³.

9. Записываем окончательный результат в виде:

V= 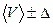V; V=(233,7 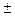15,4) мм³.

10. Относительная погрешность: .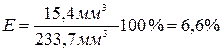

Дата добавления: 2014-12-16