Разновидности пассивного транспорта через мембрану

Перенос молекул (атомов) через мембраны, уравнение Фика.

Явления переноса – это самопроизвольные необратимые процессы, в которых благодаря молекулярному движению из одной части системы в другую переносится какая-либо физическая величина.

К явлениям переноса относятся:

- диффузия (перенос массы);

- вязкость (перенос импульса из слоя в слой);

- теплопроводность (перенос энергии);

- электропроводность (перенос электрического заряда).

Как синоним переноса частиц в биофизике используется термин транспорт частиц.

Диффузия – явление самопроизвольного переноса массы вещества из области с большей концентрацией в область с меньшей. Диффузия приводит к равномерному распределению вещества по всему объему. Количественно диффузия описывается специальными параметрами.

1. Потоком вещества ( Ф ) через элемент поверхности, который перпендикулярен направлению диффузии, называется количество этого вещества, переносимого через данный элемент за единицу времени.

Ф = - D ^.(dc/dх)^.S, где

D – коэффициент диффузии. Знак (-) означает, что поток направлен в сторону убывания концентрации вещества.

2. Плотностью потока вещества (I) называется отношение потока вещества (Ф) через элемент поверхности к площади этого элемента (S):

I =Ф/S

Подставив в эту формулу выражение для потока уравнением диффузии (уравнением Фика):

I = - D dc/dх

Знак (-) показывает, что суммарная плотность потока вещества при диффузии направлена в сторону, противоположную градиенту концентрации.

Рассмотрим в качестве примера поток незаряженных частиц через биологическую мембрану.

Обратим внимание на следующий известный факт: на границе раздела двух сред (например, воды и масла) обязательно имеет место скачкообразное изменение концентрации частиц диффундирующего вещества.

Коэффициент распределения вещества (к) – это величина, равная отношению концентраций частиц в граничащих средах:

К = с_{1 среда} / с_{2 среда}

Вещество, диффундирующее через мембрану, преодолевает три барьера (рис.6)

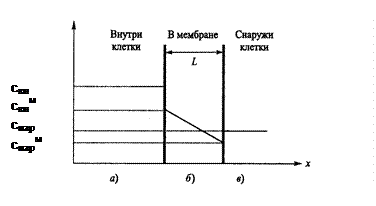
Рис. 6

а) примембранный слой,

б) саму мембрану,

в) противоположный примембранный слой.

Коэффициент распределения вещества между мембраной и окружающей средой равен коэффициенту распределения вещества между мембраной и клеткой:

к = с_нар^м/ с_нар = с _вн^м/ с_вн

Поэтому с_нар^м = к с_нар, с _вн^м = к с_вн.

Причем, величины с_нар и с_вн. можно измерить.

Учитывая малую толщину мембраны, можно считать, что концентрация молекул диффундирующего вещества изменяется в ней линейно. Поэтому градиент концентрации диффундирующего вещества постоянен:

dc/dх = (с_нар^м - с _вн^м)/L

Запишем выражение для плотности потока:

I = -D (с_нар^м - с _вн^м)/L,

или учитывая коэффициент распределения вещества, получим

I = Dк (с _вн - с_нар)/L.

Введем коэффициент проницаемости мембраны (Р)

Р = Dк/L,

который зависит от коэффициента диффузии, а также от толщины мембраны и коэффициента распределения вещества между мембраной и окружающей средой. Под проницаемостью понимают способность мембраны пропускать сквозь себя определенные вещества.

Окончательно получаем уравнение Фика для диффузии в мембранах:

I = Р(с_вн - с_нар)

6. Перенос заряженных частиц, электродиффузионное уравнение Нернста – Планка.

Рассмотрим перенос ионов. При отсутствии внешнего воздействия между поверхностями мембраны существует разность потенциалов, то есть в мембране постоянно есть электрическое поле. При отсутствии градиента концентрации главная движущая сила при переносе ионов – это электрическое поле.

На отдельный ион в электрическом поле действует сила

f₀= qE, где

Е – напряженность электрического поля, в котором находится ион, а

q = ze – заряд иона (z – валентность иона).

Если учесть, что Е = - grad φ = - dφ /dx, можно записать:

f₀= ze (dφ /dx).

На один моль ионов будет действовать сила

f = f₀N_a. = - z e N_a (dφ /dx) = - zN_a F (dφ /dx), где

N_a – постоянная Авогадро, F = e N_a - постоянная Фарадея.

Помимо электрической силы, на ионы действуют так же силы сопротивления. Поэтому движение ионов является равномерным и характеризуется средней скоростью v. Между средней скоростью движения ионов и силой, действующей на один моль, существует прямо пропорциональная зависимость:

v= u_мf, где

u_м – коэффициент пропорциональности, называемый подвижностью ионов.

Запишем

v = - u_м z F (dφ /dx),

Чтобы найти поток вещества, переносимый ионами через элемент

поверхности S, выделим цилиндрический объем электролита, ограниченный двумя такими элементами. Длину цилиндра l выразим через скорость и время:

l =vt. Объем цилиндра: V = Sl = Svt

За время t все ионы, находящиеся в цилиндре, пройдут через левую площадку S. Количество перенесенного при этом вещества равно произведению концентрации на объем: m = cV = cSvt (кг) или ν = cSvt (моль).

Найдем поток вещества Ф: Ф = cSv

Плотность потока: I = Ф/S = сv.

Используя, что v = - ν_м z F (dφ /dx), получим I = -cν_м z F (dφ /dx).

В общем случае перенос частиц определяется как градиентом их концентрации, так и воздействием электрического поля:

I = - D dc/dx - cν_м z F dφ /dx.

Это - уравнение Нернста-Планка (электродиффузионное уравнение). Оно устанавливает зависимость плотности диффузионного потока от концентрации ионов и от напряженности электрического поля.

Пассивный транспорт – перенос молекул и ионов через мембрану, который осуществляется в направлении меньшей их концентрации.

Пассивный транспорт не связан с затратой химической энергии.

Различают несколько типов пассивного транспорта. На рис. 7 представим классификацию основных видов пассивного транспорта

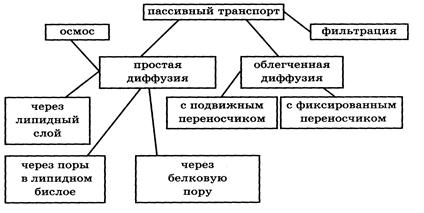
Рис.7

Рассмотрим простую диффузию, которая может происходить непосредственно через липидный бислой, через липидную или белковую пору в водном окружении.

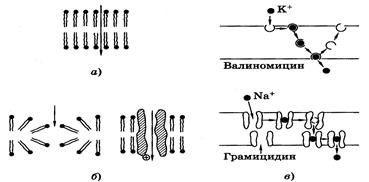
Рис.8.

На рис. 8 показаны основные разновидности простой диффузии через мембрану:

а) через липидный бислой (а);

б) через пору в липидном бислое (б);

в) через белковую пору (б).

Простая диффузия через липидный слой подчиняется уравнению Фика для молекул или в более общем случае для нейтральных и заряженных частиц – уравнению Нернста - Планка. В живой клетке такая диффузия обеспечивает прохождение кислорода и углекислого газа, ряда лекарственных веществ.

Через липидные и белковые поры проникают молекулы нерастворимых в липидах веществ и водорастворимые гидратированные ионы (окруженные молекулами воды). Для жиронерастворимых веществ и ионов мембрана выступает как молекулярное сито: чем больше размер молекулы, тем меньше проницаемость мембраны для этого вещества.

Однако простая диффузия проникает достаточно медленно и не может снабдить клетку в нужном количестве питательными веществами.

В биологических мембранах существует еще один вид диффузии – облегченная диффузия. Облегченная диффузия происходит при участии молекул переносчиков (в). Например, валиномицин – переносчик ионов калия. Установлено, что валиномицин резко повышает проницаемость мембраны для К⁺ благодаря специфике своей структуры. В нем формируется полость, в которую точно и прочно вписывается ион К⁺ (ион Na⁺ слишком велик для отверстия в молекуле валиномицина). Молекула валиномицина «захватив» ион К⁺, образует растворимый в липидах комплекс и проходит через мембрану, затем ион К⁺ остается, а переносчик уходит обратно.

При облегченной диффузии наблюдается конкуренция переносимых веществ в тех случаях, когда переносчиком переносятся разные вещества; при этом одни вещества переносятся лучше, чем другие, и добавление одних веществ затрудняет транспорт других: так, из сахара глюкоза переносится лучше, чем фруктоза, фруктоза лучше, чем ксилоза, а ксилоза лучше, чем арабиноза и т.д.

Есть вещества, блокирующие облегченную диффузию – они образуют прочный комплекс с молекулами переносчика, например, флоридзин подавляет транспорт сахаров через биологическую мембрану.

Еще разновидностью облегченной диффузии является транспорт с помощью неподвижных молекул-переносчиков, фиксированных определенным образом поперек мембраны. При этом молекула переносимого вещества передается от одной молекулы переносчика к другой, как по эстафете.

Фильтрацией называется движение раствора через поры в мембране под действием градиента давления. Скорость переноса при фильтрации подчиняется закону Пуазейля:

dV/dt = (P₁-P₂)/Х, где

- dV/dt – объемная скорость переноса раствора,

- Х – гидравлическое сопротивление.

Х = 8ηl / πr⁴,

l – длина поры, r – ее радиус, η – коэффициент вязкости раствора.

Явление фильтрации играет важную роль в процессах переноса воды через стенки кровеносных сосудов.

Осмос – преимущественное движение молекул воды через полупроницаемые мембраны (непроницаемые для растворенного вещества и проницаемые для воды) из мест с меньшей концентрацией растворенного вещества в места с большей концентрацией. Осмос – по сути дела, простая диффузия воды из мест с ее большей концентрацией в места с меньшей концентрацией воды. Осмос играет большую роль во многих биологических явлениях. Явление осмоса обуславливают гемолиз эритроцитов в гипотонических растворах.

Дата добавления: 2014-12-16