Условие задачи 1. Чему равна плотность потока формамида через плазматическую мембрану Chara ceratophylla толщиной 8 нм

ОБРАЗЦЫ РЕШЕНИЯ ЗАДАЧ

Чему равна плотность потока формамида через плазматическую мембрану Chara ceratophylla толщиной 8 нм, если коэффициент диффузии составляет 1,4^.10^-8 см²с^-1, концентрация формамида в начальный момент времени снаружи была равна 2^.10^-4 моль/л, а внутри в десять раз меньше?

Анализ условия задачи.

По условию задачи имеется плазматическая мембрана Chara ceratophylla. Известны концентрации частиц в мембране у ее внутренней и внешней поверхностях. Так как частицы не имеют заряд, то плотность потока формамида через мембрану можно определить с помощью уравнения диффузии (уравнения Фика).

c^м _сн c^м _вн

L

Запишем условие задачи и ее решение в символической форме.

Опред. j -? СИ_________

Уравнение Фика

L = 8нм L= 8^.10^-9м j = -D^. dc/dx

D = 1,4^.10^-8 см² /с D = 1,4^.10^{-12 м2} /с Учитывая малую толщину мембраны,

c^м _сн = 2^.10^-4 моль/л c^м _сн =0,2 моль/м³ можно считать, что концентрация

= 0,02 моль/ м³ молекул диффундирующего вещества,

т.е. формамида изменяется в ней

линейно. Поэтому градиент концентрации диффундирующего вещества будет равен:

dc/dx = (c^м _сн - c^м _вн)/L

Запишем выражение для плотности потока через мембрану

j = - D (c^м _сн - c^м _вн )/ L

Подставляем числовые значения, получаем

j = - 1,4^.10^{-12 м2} /с (0,2 моль/ м³ - 0,02 моль/м³ )/8^.10^{-9 м = -3,2.10-5} моль/ м²с

[j ]= [ м² моль /с^. м³• м] = [моль/ м²с]

Ответ: плотность потока формамида через мембрану составляет

j=-3,2.10^-5 моль/ м²с

Условие задачи 2.

Для изучения структуры и функции биологических мембран используют модели – искусственные фосфолипидные мембраны, состоящие из бимолекулярного слоя фосфолипида, инкрустированного белками. Толщина искусственной мембраны l = 6нм. Найдите электроемкость 1 см² такой мембраны, считая ее относительную диэлектрическую проницаемость ε_r =3.

Анализ условия задачи.

По условию задачи представленную модель можно считать плоским конденсатором, обкладками которого являются поверхностные белки, а роль диэлектрика выполняет липидный бислой. Следовательно, для определения электроемкости мембраны можно использовать формулу для определения емкости плоского конденсатора.

Запишем условие задачи и ее решение в символической форме.

Представленную по условию задачи модель биомембраны можно считать плоским конденсатором, обкладками которого служат поверхностные белки и полярные головки фосфолипидов, а диэлектриком неполярные хвосты фосфолипидов.

Опред. С –?__ СИ ___

S = 1см² S = 10^{- 4 м2}

l = 6 нм l =6^.10^{-9 м}

ε_r = 3.

ε_о = 8,84^.10^-12Ф/м.

Следовательно, определить электроемкость мембраны площадью S, можно используя формулу плоского конденсатора:

Подставим значения и вычислим С:

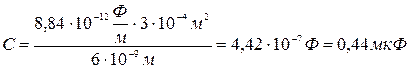
Ответ: электроемкость 1см² искусственной мембраны

С=0,44 мкФ.

Дата добавления: 2014-12-16