
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Оценочный канал ФК
|
|
|
|
Ковариационный канал ФК
Матрица измерений
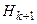 (5x28) - матрица измерений, соответствующая выражениям (4.11), ненулевые элементы которой равны:
(5x28) - матрица измерений, соответствующая выражениям (4.11), ненулевые элементы которой равны:
H1,2= 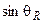 ; H1,4=1;
; H1,4=1;
H1,12=(c33kp*hkp2_1 – c32kp*hkp3_1)* 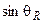 ;
;
H1,13=(c31kp*hkp3_1 – c33kp*hkp1_1)* 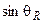 ;
;
H1,14=(c32kp*hkp1_1 – c31kp*hkp2_1)* 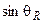 ;
;
H1,22=c23kp*hkp2_2 – c22kp*hkp3_2;
H1,23=c21kp*hkp3_2 – c23kp*hkp1_2;
H1,24=c22kp*hkp1_2 – c21kp*hkp2_2;
H2,1=1;
H2,12=c13kp*hkp2_1 – c12kp*hkp3_1;
H2,13=c11kp*hkp3_1 – c13kp*hkp1_1;
H2,14=c12kp*hkp1_1 – c11kp*hkp2_1;
H3,2=1;
H3,12=c33kp*hkp2_1 – c32kp*hkp3_1;
H3,13=c31kp*hkp3_1 – c33kp*hkp1_1;
H3,14=c32kp*hkp1_1 – c31kp*hkp2_1;
H4,3=1;
H4,22=c13kp*hkp2_2 – c12kp*hkp3_2;
H4,23=c11kp*hkp3_2 – c13kp*hkp1_2;
H4,24=c12kp*hkp1_2 – c11kp*hkp2_2;
H5,2= - 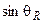 ;
;
H5,22=c23kp*hkp2_2 – c22kp*hkp3_2;
H5,23=c21kp*hkp3_2 – c23kp*hkp1_2;
H5,24=c22kp*hkp1_2 – c21kp*hkp2_2; (4.19)
 (4.20)
(4.20)
X(1:28);
X1=X(1:4,1);
X2=X(5:28,1);
Xpr(k+1)= 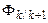 *X(k);
*X(k);
x1pr=[0;0;0;0];
Xpr(k+1)=[x1pr;X2pr];
- для автономного режима работы (когда отсутствуют данные от АВУ)
X(k+1)=Xpr(k+1)+  *z_avt(k+1); (4.21)
*z_avt(k+1); (4.21)
- для режима коррекции (когда поступают данные от АВУ, те. по приходу признака «Поступление данных от АВУ»)
X(k+1)=Xpr(k+1)+ 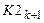 *Z2(k+1); (4.22)
*Z2(k+1); (4.22)
Примечание: ( если задача решается в фоне)
( фиксируется запаздывание dtj времени окончания вычисления оценок с момента прихода измерений и соответствующая этому запаздыванию матрица 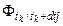 )
)
X= 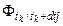 *X;
*X;
Выходные данные задачи фильтрации (управления, вырабатываемые в ФК), подаются в обратную связь:
 = 0;
= 0;
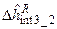 = - X(4,1)*
= - X(4,1)* 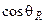 /
/ 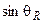 ;
;
 = [X(1,1);
= [X(1,1);  ;X(2,1)];
;X(2,1)];
 = [X(3,1);X(4,1);
= [X(3,1);X(4,1); 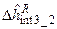 ];
];
 =
= 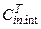
 ; -на входы соответствующих интеграторов с знаком «-«и весом: *dT/Tz (с обнулением управлений через интервал времени Tz);
; -на входы соответствующих интеграторов с знаком «-«и весом: *dT/Tz (с обнулением управлений через интервал времени Tz);
 =
= 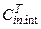
 ; -на входы соответствующих интеграторов с знаком «-«и весом: *dT/Tz (с обнулением управлений через интервал времени Tz);
; -на входы соответствующих интеграторов с знаком «-«и весом: *dT/Tz (с обнулением управлений через интервал времени Tz);
 =X(5,1);
=X(5,1);
 =[X(6,1);X(7,1);X(8,1)];
=[X(6,1);X(7,1);X(8,1)];
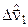 =[X(9,1);X(10,1);X(11,1)];
=[X(9,1);X(10,1);X(11,1)];
 =[X(12,1);X(13,1);X(14,1)];
=[X(12,1);X(13,1);X(14,1)];
 =X(15,1);
=X(15,1);
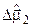 =[X(16,1);X(17,1);X(18,1)];
=[X(16,1);X(17,1);X(18,1)];
 =[X(19,1);X(20,1);X(21,1)];
=[X(19,1);X(20,1);X(21,1)];
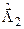 =[X(22,1);X(23,1);X(24,1)];
=[X(22,1);X(23,1);X(24,1)];
 =X(25,1);
=X(25,1);
 =X(26,1);
=X(26,1);
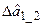 =X(27,1);
=X(27,1);
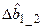 =X(28,1)/
=X(28,1)/
Коррекция КМУ (с дискретностью Tz)
 =
=  –
– 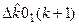 ;
;
 =
=  –
– 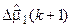 ;
;
 =
=  –
–  ;
;
 =
=  –
– 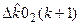 ;
;
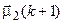 =
=  –
–  ;
;
 =
= 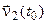 –
–  ;
;
Коррекция матрицы 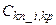 (с дискретностью Tz)
(с дискретностью Tz)
[  ;
; 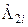 ;
; 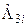 ]=
]= 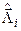 ;
;
 =[0 (-1)*
=[0 (-1)* 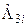
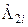 ;
;
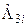 0 (-1)*
0 (-1)*  ;
;
(-1)* 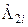
 0];
0];
 =(-1)*
=(-1)*  *
*  ;
;
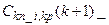 =
=  –
–  ;
;
Затем штатная процедура нормировки матрицы 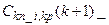 ,
,
Откуда находим текущие значения 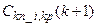 .
.
5. Результаты летных испытаний БИСО на ЭСГ на КА «Кобальт»
- для решения задачи ориентации КА используются два ЭСГ с начальной ориентацией их кинетических моментов в плоскости орбиты по корпусным осям
 блока БЧЭ;
блока БЧЭ; - контрольные витки от 28.01.2009 г;
- дискретность поступления данных от БИСО – 0.125с (8Гц);
- дискретность поступления данных от АВУ – 1 мин.
1. Исходные измерения Z2 (до коррекции положения и калибровки КМУ 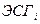 )
)

|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 518; Нарушение авторских прав?; Мы поможем в написании вашей работы!