Работа и мощность силы. Потенциальная энергия

Кинетическая энергия механической системы

ЛЕКЦИЯ 6

Производная по времени от кинетического момента механической системы относительно ее центра масс равна сумме моментов относительно центра масс всех приложенных к системе внешних сил.

Теорема об изменении кинетического момента относительно центра масс механической системы

(Изучить самостоятельно)

Подставим последний результат в теорему об изменении кинетического момента относительно неподвижного центра :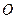

или

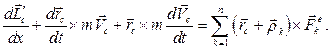
Второе слагаемое в левой части равенства равно нулю, как скалярное произведение коллинеарных сомножителей. Используя теорему о движении центра масс, получаем:

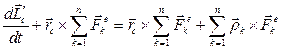
или

.

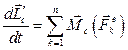Таким образом,

Половина произведения массы точки на квадрат ее скорости называется кинетической энергией материальной точки. Кинетической энергией механической системы называется сумма кинетических энергий всех ее точек.

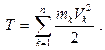(6.1)

Пусть точка движется по известной траектории; 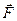– одна из сил, действующих на точку (Рис.6.1).

Элементарной работой силы называется величина, равная скалярному произведению вектора силы на элементарное перемещение точки приложения силы:

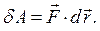(6.2)

В зависимости от используемого способа задания движения точки её скорость может быть вычислена по одной из следующих формул:

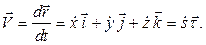
Таким образом, для вычисления элементарной работы силы получаем формулы:

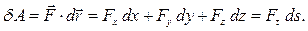
Работа силы на конечном перемещении 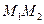определяется как сумма соответствующих элементарных работ, т.е. как криволинейный интеграл, взятый вдоль дуги 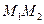траектории:

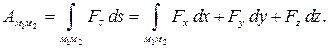(6.3)

В общем случае сила может зависеть от координат точки приложения силы, ее скорости и времени. Таким образом, для вычисления работы силы в общем случае необходимо знать траекторию точки приложения силы и закон ее движения по траектории. Однако, при решении большинства задач динамики именно закон движения точки и является искомым.

Рассмотрим силы, которые зависят только от положения точки, т.е. от ее координат, и времени. Такие силы называются позиционными. Физическое пространство, в котором на материальную точку действуют позиционные силы, называется силовым полем. В случае действия на точку позиционных сил интеграл (6.3) может быть вычислен, если известна только траектория точки приложения силы.

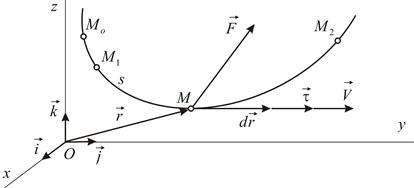
Рис.6.1

Особый класс составляют силы, работа которых не зависит от траектории, а определяется только начальным и конечным положениями точки. Такие силы называются потенциальными.

Очевидно, что вычисление интеграла (6.3) лишь по известным начальному и конечному положениям точки возможно только в том случае, когда подинтегральное выражение представляет собой полный дифференциал некоторой функции координат:

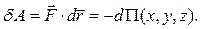(6.4)

Скалярную функцию 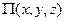называют потенциальной энергией материальной точки. Потенциальная энергия определяется из равенства (6.4) с точностью до произвольной постоянной. Выбор произвольной постоянной диктуется соображениями удобства решения конкретной задачи.

Как следует из (6.3) и (6.4), работа потенциальной силы равна разности значений потенциальной энергии в начальном и конечном положениях:

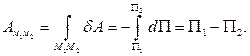(6.5)

Считая положение точки 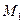произвольным и выбирая произвольную постоянную так, чтобы 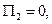получаем, что потенциальная энергия равна работе сил поля, совершённой при перемещении точки из занимаемого ею положения в некоторое нулевое.

В соответствии с равенством (6.4)

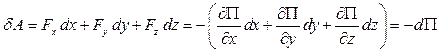
и, следовательно,

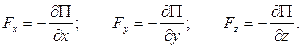
Таким образом, вектор силы в потенциальном силовом поле можно представить в виде:

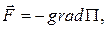
где 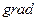– векторный оператор вида:

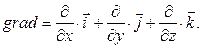
Потенциальной энергией механической системы называется сумма потенциальных энергий всех её точек.

Мощностью силы называется работа, произведённая в единицу времени:

.

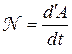Учитывая формулу (6.2), для вычисления мощности силы получаем:

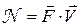, (6.6)

т.е. мощность силы равна скалярному произведению вектора силы на вектор скорости точки приложения силы.

Дата добавления: 2014-12-16