Дифференциальное уравнение вращательного движения твердого тела

Скоростью тела.

Окончательно получаем:

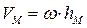(5.4)

Формула (5.4) называется формулой Эйлера. На Рис.5.5 представлено распределение скоростей точек сечения тела, перпендикулярного оси вращения.

Вычислим ускорение любой точки тела. Поскольку траектория точки окружность, находим касательное и нормальное ускорения точки:

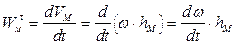
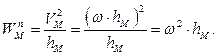
Величина 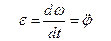называется угловым ускорением тела.

Окончательно получаем: (5.5)

На Рис.5.6 изображены составляющие вектора ускорения точки для случаев ускоренного и замедленного вращений.

Рис.5.6

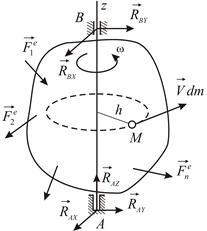
Вращение твердого тела, как и любое другое движение, происходит в результате воздействия внешних сил. Для описания вращательного движения используем теорему об изменении кинетического момента относительно неподвижного центра, записанную в проекциях на ось вращения, которую примем за координатную ось 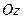(Рис.5.7):

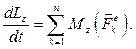(5.6)

Вычислим кинетический момент тела относительно оси вращения. Любая точка (частица) тела 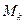описывает окружность, плоскость которой перпендикулярна оси вращения, а радиус равен кратчайшему расстоянию от точки до оси 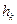. Учитывая формулу Эйлера (5.4), получаем момент количества движения точки 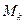относительно оси :

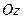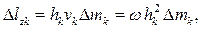
где 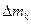– масса частицы с номером .

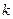Суммируя моменты количеств движения точек и переходя к пределу при массе частицы стремящейся к нулю, получаем кинетический момент тела относительно его оси вращения:

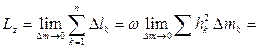
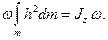(5.7)

Величина

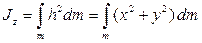(5.8)

Рис.5.7

называется моментом инерции тела относительно оси 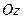. Моменты инерции характеризуют распределение массы в теле и играют существенную роль в описании движения материальных тел. Подробнее вопрос о моментах инерции будет рассмотрен ниже. Сейчас заметим только, что в рассматриваемом случае 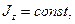так как во время вращения расстояния от точек тела до оси вращения остаются постоянными.

Подставляя результат (5.7) в равенство (5.6), получаем:

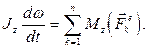(5.9)

Уравнение (5.9) называется дифференциальным уравнением вращательного движения твердого тела. Оно позволяет, зная приложенные к телу внешние силы, определить закон изменения угловой скорости тела и, следовательно, закон вращения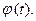

Заметим, что в уравнение (5.9) не входят неизвестные реакции шарниров 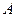и 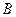, поскольку они не создают момента относительно оси вращения.

Дата добавления: 2014-12-16