Кинематика вращательного движения твердого тела

Вращение твердого тела вокруг неподвижной оси

При вращательном движении в теле существует единственная прямая, все точки которой

Рис.5.2

остаются неподвижными. Эта прямая называется осью вращения. Чтобы получить вращательное движение, можно шарнирно закрепить две точки тела (Рис.5.2).

Проведем в теле сечение, перпендикулярное оси вращения. Через любую точку сечения проведем перпендикуляр к сечению . Отрезок во все время движения остается параллельным оси вращения, т.е. движется поступательно. Таким образом, положение сечения полностью определяет положение тела в системе отсчета.

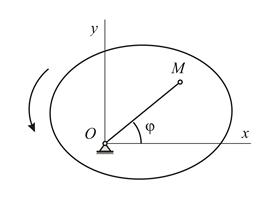
Рассмотрим движение сечения (Рис.5.3). Положение сечения полностью определяется положением любого отрезка , пересекающего ось вращения 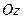. Положение отрезка , а следовательно, положение тела можно задать углом 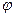, который отсчитывается от некоторой неподвижной прямой (например, оси ). Чтобы задать движение, нужно задать закон изменения угла поворота со временем:

Рис. 5.3		Рис. 5.4

Вычислим скорость любой точки тела. Траектория точки известна – это окружность с центром , лежащим на оси вращения, радиус которой равен кратчайшему расстоянию от точки до оси вращения (Рис.5.4). Вектор скорости направлен по касательной к этой окружности, т.е. перпендикулярен отрезку . Дугу 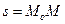можно рассматривать как дуговую координату точки. Длина дуги окружности связана с центральным углом формулой

Принимая во внимание формулу (2.4), получаем:

Рис.5.5

Величина называется угловой

Дата добавления: 2014-12-16