Теоретичні питання оптимізації діяльності підприємства

Фахівці різних сфер у своєї діяльності часто використовують моделювання. У багатьох організаціях для оцінки капітальних вкладень використовують різні моделі фінансових потоків; при призначені цін на товари явно чи неявно використовують моделі еластичності попиту, менеджери активно використовують інвестиційні моделі. Названі задачі вирішуються і на підприємствах ресторанного господарства. Крім того, у підприємств ресторанного господарства є значна кількість задач, які мають багатоваріантні рішення, що залежать від врахування впливу значної кількості змінних факторів. Наприклад, задачі планування загальної діяльності, складання виробничої програми підприємства, раціоналізація транспортних витрат, розподіл робіт на підприємстві та його структурних підрозділах між працівниками та оптимізація витрат на заробітну плату і т. ін.

Помилки у прийнятті рішень за такими складними задачами можуть обернутися значними фінансовими збитками, банкрутством. Сьогоднішня альтернатива підготовки рішень з складних питань – моделювання за допомогою комп’ютера. Помилки тоді залишаються на папері.

Модель [Model, Simulator] — матеріальний об’єкт, система матема­тичних залежностей або програма, що імітують структуру або функ­ціонування досліджуваного об’єкта. Основна вимога до моделі - її адекватність об’єкту.

При прийнятті рішень виконуються наступні етапи:

Процес моделювання при прийнятті управлінських рішень (перші два етапи) наведений на рис. 5.1.

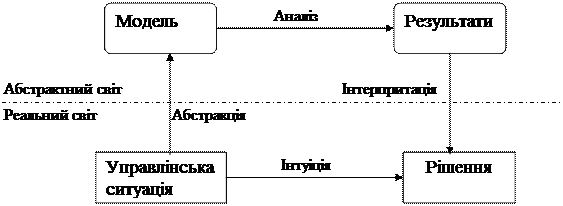Рисунок 5.1 – Процес моделювання при прийнятті управлінських рішень

Процес моделювання, доповнений досвідом та інтуїцією фахівця, дозволяє прийняти більш вдале рішення й багато чому навчитися. Саме тому процес моделювання й прийняття рішень фахівцем неможна розривати.

Примітка. Існує три типи моделей – фізичні (макети літаків, міст…), аналогові (карта основних шляхів є аналоговою моделлю території, кругова діаграма, графік…), символічні або математичні.

Дуже часто при розв’язанні задач виробництва необхідно знайти найкраще значення показника (максимізувати прибуток, мінімізувати витрати…) при наявності обмежених ресурсів. Такі задачі є оптимізаційними задачами.

Відповідно, оптимізаційна модель – детермінована модель прийняття рішень, що містить показник ефективності (цільову функцію), яку необхідно оптимізувати при умові дотримання набору заданих параметрів.

Оптимізація – мінімізація або максимізація цільової функції.

Оптимізаційні моделі складаються з трьох складових.

1. Цільова функція чи критерій оптимізації, показує, у якому змісті рішення повинне бути оптимальним, тобто найкращим. При цьому можливі 3 види призначення цільової функції:

1) максимізація;

2) мінімізація;

3) призначення заданого значення.

2. Обмеження встановлюють залежності між змінними. Вони можуть бути як однобічними, наприклад:

, так і двосторонніми .

При рішенні задачі оптимізації за допомогою Ехсеl таке двостороннє обмеження записується у виді двох однобічних обмежень

,

3. Межові умови показують, у яких межах можуть бути значення шуканих змінних в оптимальному рішенні.

Рішення задачі, що задовольняє всім обмеженням і межовим умовам, називається припустимим. Якщо математична модель задачі оптимізації складена правильно, то задача буде мати цілий ряд припустимих рішень. Пояснимо це положення. Важливою характеристикою задачі оптимізації є її розмірність, обумовлена числом змінних n і числом обмежень m. Співвідношення цих величин є визначальним при постановці задачі оптимізації. Можливі три співвідношення n<m, n=m, n>m.

1. Якщо n<m, то такі задачі рішення не мають.

2. Якщо n=m, то таке співвідношення n і m — це необхідна умова для рішення системи лінійно-незалежних рівнянь.

3. Якщо n>m, то може бути незліченна безліч значень X_i які задовольняють даній системі рівнянь.

Таким чином, умова n>m — це неодмінна вимога для задач оптимізації. Помітимо, що таку систему рівнянь, для яких n=m, можна розглядати як задачу оптимізації, що має одне припустиме рішення, і вирішувати її як звичайну задачу оптимізації, призначаючи як цільову функцію будь-яку перемінну.

Оптимальне рішення — це найкраще. Але рішення, найкращого у всіх змістах, бути не може. Воно може бути найкращим, тобто оптимальним, тільки в одному, строго встановленому змісті. У реальних обставинах можливі інші варіанти.

Приймаючий рішення повинний абсолютно точно уявляти, у чому полягає оптимальність рішення, тобто за яким критерієм (цільовою функцією) прийняте рішення повинне бути оптимальним.

У загальному випадку за допомогою критерію можна оцінювати якості як бажані (наприклад, прибуток, продуктивність, надійність), так і небажані (загальні витрати, витрата матеріалу, простої устаткування). Тоді в першому випадку прагнуть до максимізації критерію, а в другому — до його мінімізації.

Дата добавления: 2014-12-16