Рекурсивный алгоритм

Списки смежности

Для каждой вершины vÎV имеется список вершин, таких, что существует ребро/дуга (v,u). Рассмотрим примеры списков смежности:

для рис. 4.1
	для рис. 4.3

Число ячеек памяти в этом случае всего n+m. Неудобство заключается в том, что когда необходимо определить, есть ли ребро из v в u, приходится просматривать весь список, соответствующий v.

На С++ данную структуру можно представить следующим образом:

а) с помощью массива списков

struct list {int inf; list *next;};

list * graph [10]; // описание массива списков

Данная структура представляет собой одномерный массив, каждый элемент которого является указателем на список смежности. Способ доступа к элементам списка можно организовать по принципу стека, очереди или списка с произвольным доступом, в зависимости от предпочтений программиста.

б) с помощью списка списков:

struct list {int inf; list *next;};

struct graph {int vertex; list *nextAdjacent; graph *following;};

graph *firstGraph; // описание списка списков

Каждый элемент структуры graph хранит номер вершины vertex, указатель на список смежных с ней вершин sp и указатель на следующую вершину в графе gr. При работе с такой структурой приходится обрабатывать два списка, способ доступа к элементам этих списков можно организовать по принципу стека, очереди или списка с произвольным доступом, в зависимости от предпочтений программиста.

Замечание. При рассмотрении алгоритмов обработки данных, представленных в виде графа, мы будем использовать представление графа в виде матрицы смежности. Читателям предлагается самостоятельно модифицировать предложенные ал горитмы для других способов представления графов.

4.3. Алгоритмы обхода графов

При решении многих задач с использованием графов необходимо уметь обходить все вершины и ребра (дуги) графа. Уточним, обойти граф – это побывать во всех его вершинах точно по одному разу. Существует два классических алгоритма обхода графа: обход графа в глубину и обход графа в ширину. Рассмотрим эти алгоритмы подробно.

4.3.1. Обход (поиск) в глубину

Замечание. Данный алгоритм является обобщением обхода дерева в прямом порядке.

Предположим, что есть граф G, в котором первоначально все вершины помечены меткой «не просматривалась». Начинаем обход с произвольной вершины 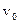, для которой метка «не просматривалась» меняется на метку «просматривалась». Затем для каждой вершины, смежной с вершиной 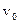и ранее не просмотренной, рекурсивно применяем алгоритм обхода в глубину. Когда все вершины достижимые из 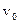будут просмотрены, рекурсия заканчивается. Если некоторые вершины графа остались не просмотренными, то выбираем одну из таких вершин и снова запускаем алгоритм обхода. Этот процесс продолжается до тех пор, пока обходом не будут просмотрены все вершины данного графа.

Этот метод обхода вершин графа называется поиском в глубину, поскольку поиск непросмотренных вершин идет в направление вперед (вглубь) до тех пор, пока это возможно.

Для того, чтобы отличить просмотренные вершины от непросмотренных, вводим массив used [n], чьи элементы будут принимать только два значения: 1 - если вершина не просмотрена, и 0 в противном случае.

Рассмотрим подпрограмму dfs (depth-first search), реализующую данный алгоритм. Формальным параметром является v – вершина, от которой начинается обход. Граф задается матрицей смежности, которая является глобальной переменной. Массив used также является глобальной переменной.

void dfs (int v)

{ int u;

out<<v<<"\t"; //просматриваем текущую вершину, к v добавляем 1 для

// удобства восприятия информации (напомним, массивы

// в С нумеруются с нуля)

used[v]=0; // помечаем ее как просмотренную

for (u=0; u<n; u++) // просматриваем строку с номером v в матрице смежности

if (gr[v][u] && used[u]) // если в столбце u строки v стоит 1, то вершины v и u

// смежные, если к тому же вершина u в массиве меток

// помечена как не просмотренная,

dfs(u);

}

Рассмотрим пример использования подпрограммы dfs.

#include <fstream>

using namespace std;

ifstream in("input.txt");

ofstream out("output.txt");

int n; // размерность графа

int **gr; //матрица смежности

int *used; // матрица меток

void dfs (int v)

{ int u;

out<<v+1<<"\t"; //просматриваем текущую вершину, к v добавляем 1 для

// удобства восприятия информации (напомним, массивы

// в С нумеруются с нуля)

used[v]=0; // помечаем ее как просмотренную

for (u=0; u<n; u++) // просматриваем строку с номером v в матрице смежности

if (gr[v][u] && used[u]) // если в столбце u строки v стоит 1, то вершины v и u

// смежные, если к тому же вершина u в массиве меток

// помечена как не просмотренная,

dfs(u);

}

void main ()

{ int i,j;

in>>n; // считываем размерность массива

used=new int [n]; // выделяем память под массив меток

gr=new int* [n]; // выделяем память под количество строк в массиве смежности

// для каждой i-той строки матрицы, которая соответствует i-1-той вершине графа

for (i=0; i<n; i++)

{used[i]=1; // помечаем вершину как не просмотренную

gr[i]=new int [n]; // выделяем память под i-тую строку матрицы смежности

for (j=0; j<n; j++) // вводим эту строку из файла f

in>>gr[i][j]; }

for (i=0; i<n; i++) // для каждой вершины графа

if (used[i]) // если она не просмотрена

dfs(i); // вызываем рекурсивную функцию обхода в глубину, которая

// просматривает текущую вершину и вершины, достижимые из данной

in.close();

out.close();

// освобождаем память, занимаемую массивами

delete used;

for (i=0; i<n; i++) delete gr[i];

delete gr;

}

В первой строчке входного файла должна быть записана размерность матрицы смежности (количество вершин графа), далее – сама матрица.

Если во входном файле записать матрицу смежности, соответствующую графу с рис. 4.1, то в выходном файле будет записано: 1 2 4 3 4.

Если во входном файле записать матрицу смежности, соответствующую графу с рис. 4.3, то в выходном файле будет записано: 1 2 4 3 5 6.

Дата добавления: 2014-12-16