Нерекурсивный алгоритм

При обходе графа в глубину, чем позже просмотрена вершина, тем раньше она используется потом, когда у текущей вершины не окажется смежных непросмотренных вершин и приходится возвращаться на шаг назад. Поэтому, используя для хранения просмотренных вершин стек, можно избавиться от рекурсии.

Начинаем обход с произвольной вершины 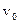, помечаем ее как просмотренную и кладем в стек. Далее отыскиваем вершину, смежную с 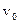и еще не просмотренную, отмечаем ее как просмотренную, кладем ее в стек и повторяем вышеописанные действия для нее. Если у вершины v не окажется смежных непросмотренных вершин, то удаляем ее из стека и рассматриваем следующую вершину, которая есть в стеке (т.е. вершину, из которой попали в v). Т. о. продолжаем до тех пор, пока стек не окажется пустым.

Рассмотрим процедуру dfs, реализующую данный алгоритм. Формальным параметром процедуры является v – вершина, от которой начинается обход. Граф задается матрицей смежности, которая является глобальной переменной. Массив used также является глобальной переменной. Для реализации стека используем стек из библиотеки STL.

void dfs (int v)

{ int u, b, i;

stack <int> s; // инициализируем стек

s.push(v); // помещаем в стек номер вершины, с которой нашали обход

out<<v+1<<"\t"; // вводим номер просмотренной вершины на экран

used[v]=0; // помечаем вершину как просмотренную

while (!s.empty()) // пока стек не пуст

{b=1; // флаг, примет значение 0, если мы найдем для

// данной вершины смежную непросмотренную вершину

i=s.top(); // считываем из стека (без извлечения) номер текущей

// просматриваемой вершины,

for (u=0; u<n && b;) // просматриваем строку, соответствующую этой

// вершине в матрице смежности

if (gr[i][u] && used[u]) // если находим смежную непросмотренную вершину,

b=0; // то останавливаемся на этой вершине,

else u++; // иначе продолжаем поиск

if (!b) // если для вершины i нашли смежную непросмотренную вершину,

{s.push(u); // то помещаем ее в стек

out<<u+1<<"\t"; // выводим на экран

used[u]=0; } // и помечаем как просмотренную

else s.pop(); // если b=1, то для вершины i смежных непросмотренных

// вершин нет и мы удаляем эту вершину из стека

}

}

Если во входном файле записать матрицу смежности соответствующую графу с рис. 4.1, то в выходном файле будет записано: 1 2 4 3 4.

Если во входном файле записать матрицу смежности соответствующую графу с рис. 4.3, то в выходном файле будет записано: 1 2 4 3 5 6.

Таким образом, результаты нерекурсивного обхода в глубину совпадают с результатами рекурсивного обхода.

4.3.2. Обход (поиск) в ширину

Этот метод обхода получил свое название из-за того, что при достижении в процессе обхода вершины v далее рассматриваются все вершины, смежные с ней. Таким образом, при обходе в ширину, чем позже просмотрена вершина, тем позже она используется. Поэтому для хранения просмотренных вершин используется очередь.

Начинаем обход с произвольной вершины 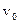, отмечаем ее как просмотренную, кладем в очередь. Все вершины, смежные с данной, помещаем в очередь и отмечаем как просмотренные. Удаляем вершину 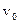из очереди. Берем первую вершину v из очереди, записываем в очередь все вершины, смежные с ней, и удаляем из очереди саму вершину v. Алгоритм работает до тех пор, пока очередь не оказывается пустой.

Рассмотрим процедуру bfs (breadth-first search), реализующую данный алгоритм. Формальным параметром процедуры является v – вершина, от которой начинается обход. Граф задается матрицей смежности, которая является глобальной переменной. Массив used также является глобальной переменной. Для реализации очереди используем очередь из библиотеки STL.

void bfs (int v)

{ int u;

queue <int> q; // описываем указатель на очередь

// инициализируем очередь

q.push(v); // помещаем вершину v в очередь

used[v]=0; // помечаем ее как просмотренную

while (!q.empty()) // пока очередь не пуста

{v=q.front(); // запоимнаем верхнюю вершину из очереди

q.pop();//удаляем вершину из очереди

out<<v+1<<"\t"; // выводим ее на печать

for (u=0; u<n;u++) // просматриваем для вершины v матрицу смежности

if (gr[v][u] && used[u]) // если находим смежную непросмотренную вершину,

{q.push(u); // то помещаем ее в очередь

used[u]=0; } // и помечаем как просмотренную

}

}

Если во входном файле записать матрицу смежности соответствующую графу с рис. 4.1, то в выходном файле будет записано: 1 2 4 3 5.

Если во входном файле записать матрицу смежности соответствующую графу с рис. 4.3, то в выходном файле будет записано: 1 2 4 6 3 5.

Полученные результаты несколько отличаются от результатов алгоритма обхода в глубину. Если во входном файле будут записаны данные, соответствующие графу с более сложной структурой, то и отличия будут более сильные.

4.6. Решение практических задач с использованием графов

1. В файле input.txt задана матрица смежности графа (в первой строке – размерность матрицы, затем сама матрица) и вершина а. Вывести в файл output.txt все вершины, смежные с a.

_____________________________prim1.cpp_______________________________

#include <fstream>

using namespace std;

void main ()

{

ifstream in("input.txt");

ofstream out("output.txt");

int n; // число вершин в графе

int **gr; // указатель на матрицу смежности графа

int i,j,a;

in>>n; // считываем размерность массива

gr=new int* [n]; // выделяем память под количество строк в массиве смежности

// для каждой i-той строки матрицы, которая соответствует i-1-той вершине графа

for (i=0; i<n; i++)

{

gr[i]=new int [n]; // выделяем память под i-тую строку матрицы смежности

for (j=0; j<n; j++) // вводим эту строку из файла f

in>>gr[i][j];

}

in>>a;

// просматриваем в матрице смежности строку, соответствующую вершине а

for (j=0; j<n; j++)

if (gr[a-1][j]!=0) // если в просматриваемой позиции стоит не ноль, то вершины

// соединены ребром, т.е. соседние

out<<j+1<<"\t"; // записываем вершину j в файл

in.close();

out.close();

// освобождаем память, занимаемую массивами

for (i=0; i<n; i++)

{

delete gr[i];

}

delete gr;

}

______input.txt_____________

0 1 0 1 0 1

1 0 0 0 0 0

0 0 0 1 0 0

1 0 1 0 1 1

0 0 0 1 0 1

1 0 0 1 1 0

_____________________________output.txt________________________________

1 3 5 6

Замечания

Данные, приведенные в файле input.txt, соответствуют рис.4.3.

Напоминаем, т.к. в С массивы нумеруются с нуля, то вершине с номером k в матрице смежности будет соответствовать строка/столбец с номером k-1, а строке/столбцу с номером w будет соответствовать вершина с номером w+1.

2. В файле input.txt задана матрица смежности графа (в первой строке – размерность матрицы, затем сама матрица) и вершина а. Вывести в файл output.txt все вершины, достижимые из вершины а.

_____________________________prim2.cpp_______________________________

#include <fstream>

using namespace std;

ifstream in("input.txt");

ofstream out("output.txt");

int n; // размерность графа

int **gr; //матрица смежности

int *used; // матрица меток

void dfs (int v)

{ int u;

out<<v+1<<"\t";

used[v]=0;

for (u=0; u<n; u++)

if (gr[v][u] && used[u])

dfs(u);

}

void main ()

{ int i,j,a;

in>>n;

used=new int [n];

gr=new int* [n];

for (i=0; i<n; i++)

{used[i]=1;

gr[i]=new int [n];

for (j=0; j<n; j++)

in>>gr[i][j]; }

in>>a;

dfs(a-1); //запускаем алгоритм обхода для данной вершины

//после его завершения будут помечены и выведены в файл все вершины, достижимые от данной

in.close();

out.close();

delete used;

for (i=0; i<n; i++) delete gr[i];

delete gr;

}

______input.txt_____________

0 1 0 1 0

1 0 0 0 0

0 1 0 0 0

0 0 1 0 0

1 0 0 1 0

_____________________________output.txt________________________________

4 3 2 1

Замечание. Данные, приведенные в файле input.txt, соответствуют рис.4.1.

Дата добавления: 2014-12-16