Элементы корреляционного анализа

Задача 4.

По 14-ти предприятиям городского хозяйства (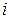 - порядковый номер предприятия) имеются соответствующие данные об объеме продукции (услуг) за месяц ( 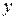млн.руб.) и уровне механизации труда (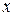, %). Статистические данные приведены в таблице.

Для выявления наличия корреляционной связи между объемом продукции и уровнем механизации труда требуется:

1) измерить тесноту связи между признаками с помощью коэффициента корреляции рангов Спирмена;

2) проверить его достоверность на уровне значимости ;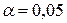

3) построить аналитическую таблицу и дать графическое изображение линии связи.

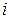
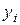
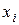
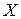С помощью выборочного коэффициента ранговой корреляции Спирмена оценивается теснота связи между двумя качественными переменными и 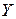. Этот коэффициент применяется и в случае количественных переменных, если заранее не гарантируется нормальность распределения двумерной случайной величины .

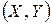Выборочный коэффициент служит точечной оценкой генерального коэффициента ранговой корреляции 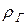. Коэффициенты и 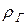изменяются от минус единицы до плюс единицы. Чем ближе 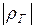к 1, тем теснее связь между переменным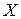и и .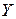

1. Для того, чтобы вычислить коэффициент ранговой корреляции 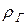, нужно сначала провести ранжировку объектов и получить две согласованные последовательности рангов.

Расположим наблюдаемые пары в порядке невозрастания качества по показателю :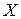

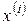
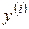
Затем пронумеруем объекты (числа) в каждой из строк в порядке неубывания. Рангом объекта называется его номер в ранжировке. Получим следующую таблицу:

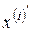
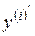
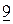
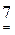
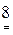
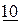
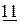
В первой ранжировке обведены группы объектов, имеющих одинаковое качество по переменной 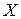; во второй ранжировке единообразно отмечены объекты, имеющие одинаковое качество по переменной .

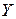Далее объектам одинакового качества присваиваем средние ранги (средние арифметические порядковых номеров этих объектов). В результате получим две согласованные последовательности рангов:

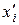
	1,5	1,5	3,5	3,5			7,5	7,5					13,5	14,5
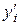
		7,5	7,5
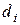
	-8,5	-6	-4	-6,5	-5	-8	1,5	-5,5					1,5	13,5

В последней строке записаны разности рангов .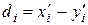

Найдем сумму квадратов разностей рангов: 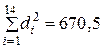и по известной формуле вычислим выборочный коэффициент ранговой корреляции Спирмена:

.

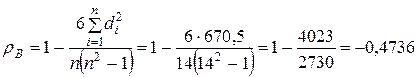2) Для проверки статистической значимости выборочного коэффициента ранговой корреляции Спирмена на заданном уровне значимости 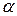выдвигается гипотеза 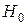об отсутствии ранговой корреляционной связи:

.

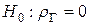Для проверки выдвинутой гипотезы используется статистика Стьюдента

,

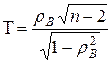где 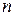– число пар в выборке.

При условии справедливости гипотезы 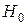случайная величина 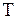имеет известное 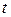-распределение Стьюдента с степенями свободы.

Зная , вычисляем наблюдаемое значение статистики Стьюдента:

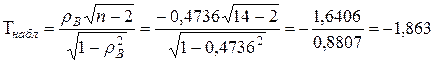
и число степеней свободы .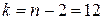

По таблице критических точек распределения Стьюдента для двусторонней критической области находим критическую точку статистики Стьюдента (см. например [4]),

.

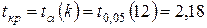Критерий проверки:

1. Если 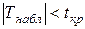, то гипотеза 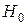сохраняется (ранговая корреляционная связь практически отсутствует);

2. Если 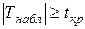, то гипотеза 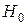отвергается (существует значимая корреляционная связь между переменным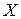и и ).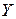

В нашем случае 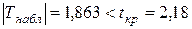, поэтому в соответствие с критерием проверки заключаем, что 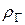незначимо отличается от нуля, т.е. ранговая корреляционная связь практически отсутствует.

Дата добавления: 2014-12-16