Линейные дифференциальные уравнения. Метод вариации произвольной постоянной

Дифференциальные уравнения с разделяющимися переменными. Однородные уравнения

Дифференциальные уравнения первого порядка, его частное и общее решения (интегралы). Теорема Коши существования и единственности решения начальной задачи. Геометрический смысл дифференциального уравнения. Метод изоклин

Рассмотрим дифференциальное уравнение первого порядка:

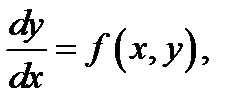
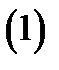
где неизвестная функция. Областью определения уравнения (1) называется множество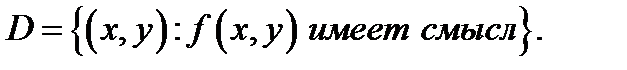

Определение 1. Функция 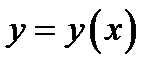называется решением уравнения (1) на отрезке[1] 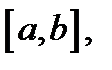если выполнены следующие условия:

1) точка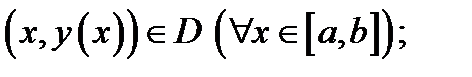

2) функция 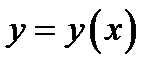дифференцируема на отрезке 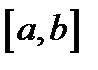и имеет место тождество

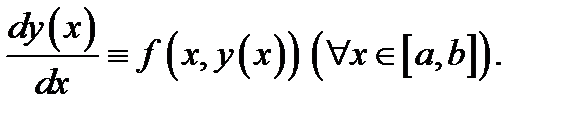
График решения 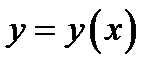называется интегральной кривой уравнения (1). Например, функция 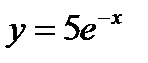является решением уравнения 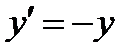на всей числовой оси (проверьте это!). Часто вместо слов “ решить уравнение” говорят “проинтег-

рировать уравнение”.

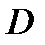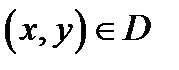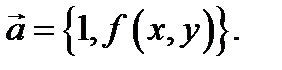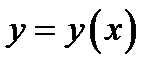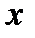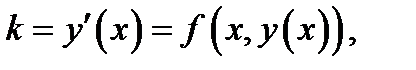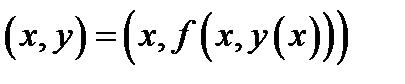Пусть – область определения уравнения (1). Тогда в каждой точке мы можем построить вектор Поскольку угловой коэффициент интегральной кривой в фиксированной точке равен то вектор касается в точке интегральной кривой. Важно заметить, что саму интегральную кривую можно и не знать, а вектор всегда известен. Таким образом, уравнение задаёт в своей области определения множество векторов 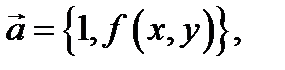которое называют векторным полем (или просто полем) дифференциального уравнения (1). В этом и состоит геометрический смысл уравнения (1).

В связи с этим задачу интегрирования дифференциального уравнения (1) можно свести к построению кривых, касающихся в каждой своей точке векторного поля 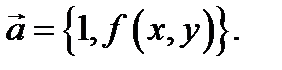На такой интерпретации уравнения (1) основан геометрический метод решения, называемый методом изоклин. Поясним его смысл.

Определение 2. Кривая задаваемая уравнением 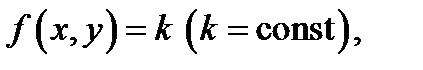называется изоклиной уравнения (1).

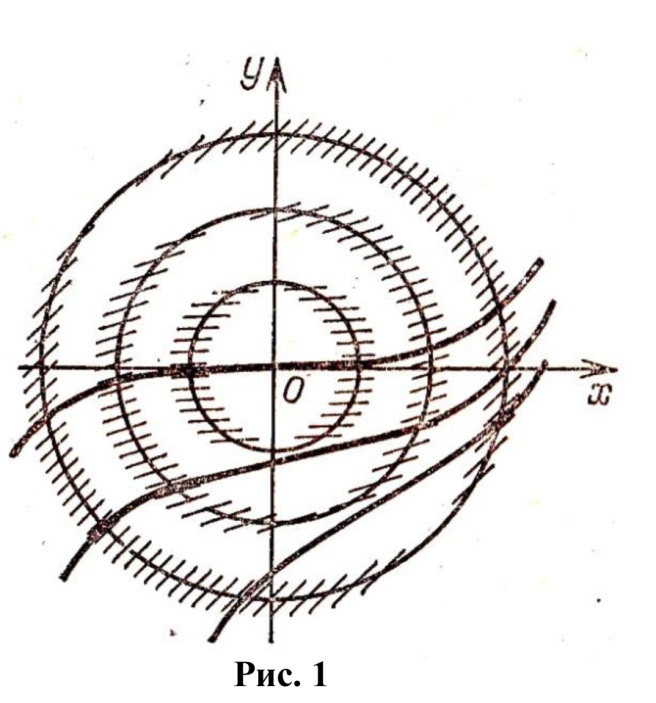
Из геометрического смысла уравнения (1) вытекает, что все его интегральные кривые в произвольной точке изоклины 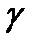имеют касательные векторы одного и того же наклона (см. рис.1). Построив довольно густую сетку изоклин (с различными постоянными 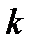) и изобразив на них векторы 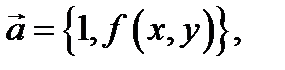мы, двигаясь от фиксированной точки 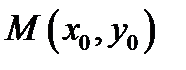с изображенным на ней вектором проводим эскиз кривой, которая коснется вектора на следующей ближайшей изоклине, и т.д. В результате будет нарисована приближенная интегральная кривая уравнения (1) (на рис. 1 изображены не сами векторы 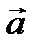, а их небольшие отрезки).

Рассматривая уравнение видим, что оно имеет бесконечное множество реше-

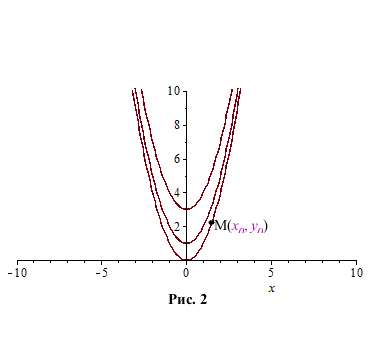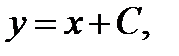ний где 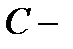произвольная постоянная. Такая ситуация имеет место для любого дифференциального уравнения. Для выделения конкретного решения надо задать вместе с равнением (1) ещё так называемое начальное условие 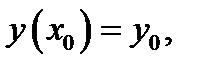означающее, что при 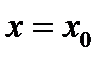решение должно иметь значение 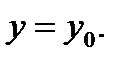Полученная задача называется начальной задачей или задачей Коши и её кратко записывают так:

Геометрически задача Коши означает, что среди всех интегральных кривых уравнения (1) надо найти ту, которая проходит через заданную начальную точку 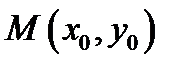(см. рис. 2). В каком случае задача Коши (2) имеет решение и будет ли оно единственным? Ответ на этот вопрос содержится в следующем утверждении, которое мы даём без доказательства.

Теорема Коши (существования и единственности решения начальной задачи). Пусть в уравнении (1) правая часть 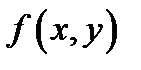и её частная производная 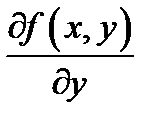непрерывны в области определения 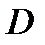уравнения (1). Тогда какова бы ни была начальная точка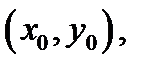

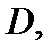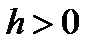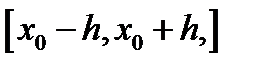лежащая внутри области существует число такое, что начальная задача (2) с указанной начальной точкой имеет на отрезке решение и это решение единственно на этом отрезке.

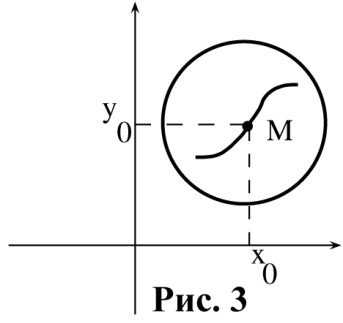
Геометрически это означает, что при выполнении условий теоремы Коши существует окрестность начальной точки 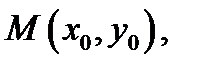в которой содержится лишь одна интегральная кривая уравнения (1), проходящая через точку (см. рис. 3). Сделаем два замечания.

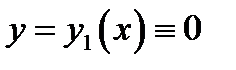Замечание 1. Теорема Коши носит достаточный характер. Это означает, что при выполнении её условий решение задачи (2) обязательно существует и единственно. Однако решение может существовать и тогда, когда не выполняются условия этой теоремы. Правда, в этом случае не гарантируется единственность решения. Например, задача Коши имеет два решения: и

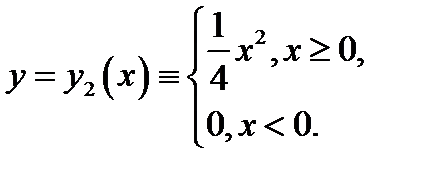
В этой задаче правая часть 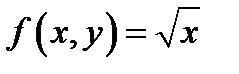не удовлетворяет условиям теоремы Коши: в окрестности начальной точки 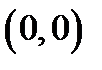частная производная не существует.

Замечание 2. Теорема Коши носит локальный характер. Это означает, что при выполнении её условий существование решения гарантируется лишь в достаточно малой окрестности точки (число вообще говоря, достаточно мало̀).

Перейдём теперь к описанию частного и общего решений и интегралов.

Определение 3. Частным решением уравнения (1) называется решениекакой-нибудь его фиксированной задачи Коши (2), а частным интегралом этого уравнения называется

частное решение 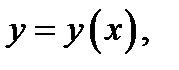записанное в неявной форме

Например, функция является частным решением уравнения 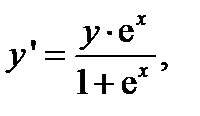а соотношение 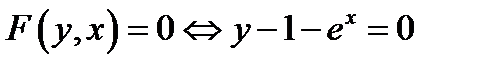– частным интегралом того же уравнения.

Определение 4. Общим решением уравнения (1) в области 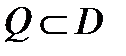( 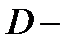область определения уравнения (1))называется функция удовлетворяющая следующим требованиям:

1) какова бы ни была допустимая постоянная 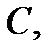функция 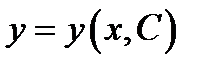является решением уравнения (1) на некотором отрезке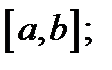

2) какова бы ни была начальная точка 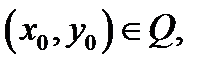существует значение 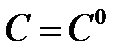постоянной такое, что функция 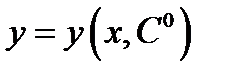является решением задачи Коши (2) с этой начальной точкой.

Общим интегралом уравнения (1) называется общее решение, записанное в неявной форме

Чтобы проверить, будет ли соотношение общим интегралом уравнения (1), надо из системы уравнений

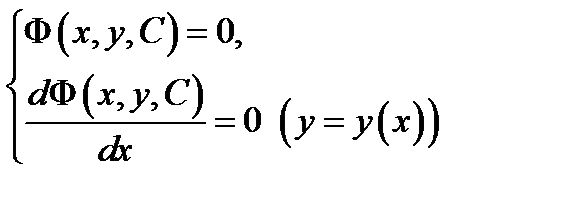
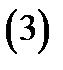
исключить постоянную Если при этом будет получено дифференциальное уравнение (1) (или эквивалентное ему уравнение), то – общий интеграл уравнения (1).

Пример 1. Проверить, что соотношение 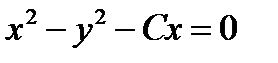является общим интегралом уравнения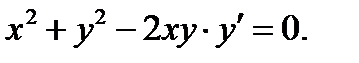

Решение. Составляем систему (3) и исключаем постоянную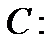

Получено данное дифференциальное уравнение, значит, 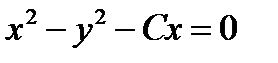– его общий интеграл.

Опишем теперь аналитические методы решения некоторых дифференциальных уравнений.

1. Уравнения с разделенными переменными: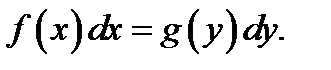

Ясно, что общий интеграл этого уравнения может быть получен интегрированием обеих частей (функции и непрерывны в своих областях определения):

Отметим, что здесь часто вместо определенных интегралов пишут неопределенные.

2. Уравнения с разделяющимися переменными:

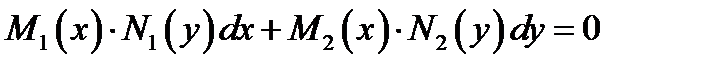
(здесь перед дифференциалами стоят произведения функций с разделёнными переменными).

Предполагая, что функции 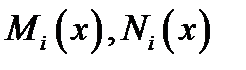непрерывны в своих областях определения, разделим обе части уравнения (4) на произведение 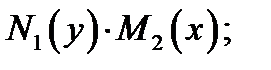будем иметь

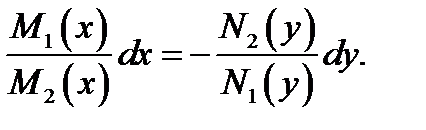
Получено уравнение с разделёнными переменными. Интегрируя его, получим общий интеграл

Однако это верно в случае, когда Случа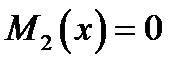и или 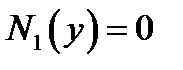надо рассматривать отдельно. Если при этом будут получены решения уравнения (4), то их надо присовокупить к уже полученным.

Пример 2. Решить уравнение

Решение. Разделяем переменные, поделив обе части уравнения на произведение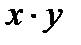

и интегрируем полученное уравнение:

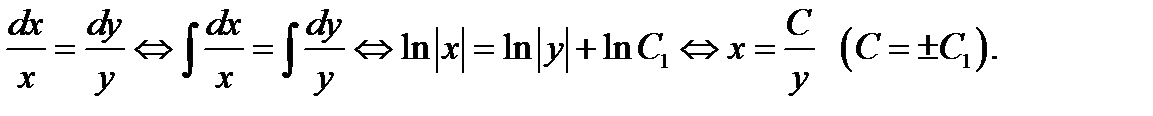
Рассматриваем отдельно случа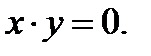й При 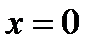исходное уравнение обращается в тождество, значит, 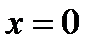– решение. Оно может быть получено из при 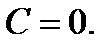Функция 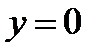также удовлетворяет данному уравнение. Однако она не может быть получена из . Следовательно, решениями исходного уравнения является совокупность функций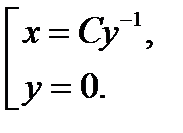

3. Однородные уравнения: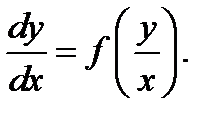

Такие уравнения приводятся к уравнению с разделяющимися переменной заменой 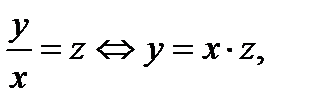где новая неизвестная функция. Действительно, дифференцируя замену и подставляя её в исходное уравнение, будем иметь

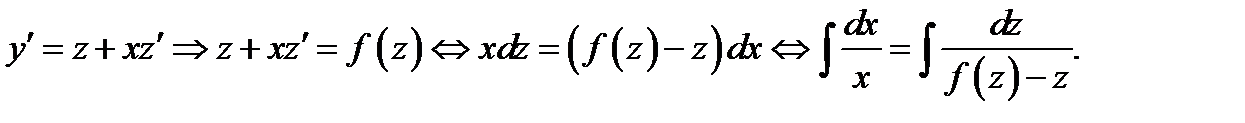
Заметим, что к однородным приводятся уравнения вида

В первом случае надо разделить числитель и знаменатель входящей под знак функции дроби на 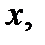во втором случае сделать замену переменных 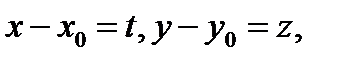где 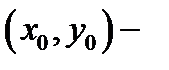решение системы уравнений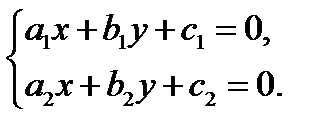

Пример 3. Решить уравнение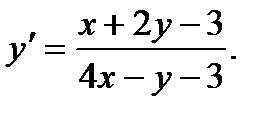

Решение. Найдем решение системы 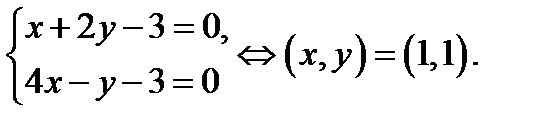Делаем замену переменных 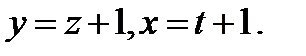Вместо исходного получим следующее уравнение:

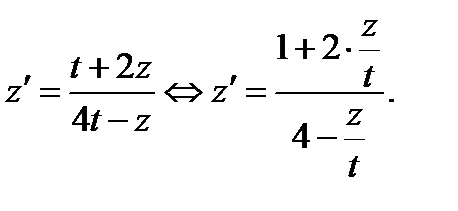jj

Это уравнение однородно, поэтому делаем замену В итоге получим уравнение 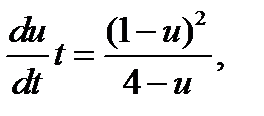решая которое методом разделения переменных, будем иметь

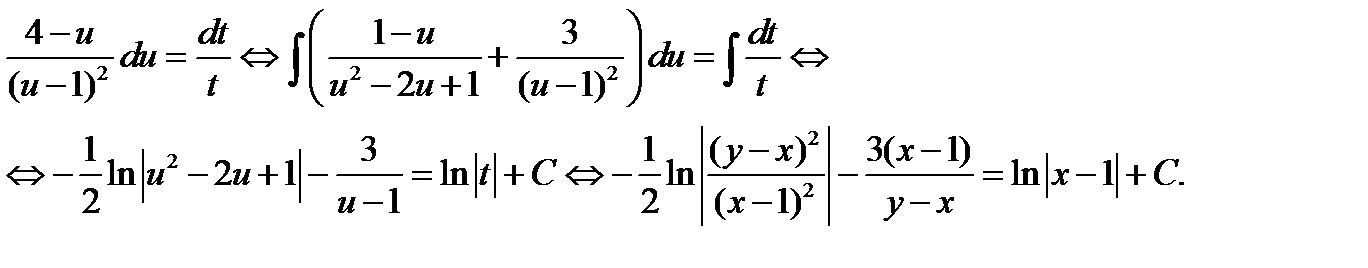
Получен общий интеграл данного уравнения.

Лекция 2. Линейные уравнения первого порядка. Дифференциальные уравнения высшего порядка. Задача Коши. Теорема существования и единственности решения задачи Коши. Общее решение и общий интеграл. Методы понижения порядка дифференциального уравнения

Наиболее часто встречаются линейные дифференциальные уравнения. Так называются уравнения, у которых правая часть линейна относительно неизвестной функции. Перейдём к их рассмотрению.

Уравнение вида

где 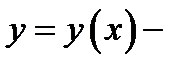неизвестная функция, известные функции[2], называется линейным дифференциальным уравнением. Если 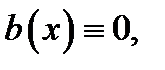то уравнение (1) называется однородным. Если 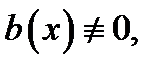то (1) называют неоднородным уравнением. Часто 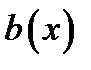называют свободным членом уравнения (1) или неоднородностью.

Теорема 1. Пусть в уравнении (1) функции 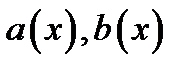непрерывны на отрезке Тогда уравнение (1) с начальным условием имеет на отрезке

единственное решение и это решение может быть записано в виде

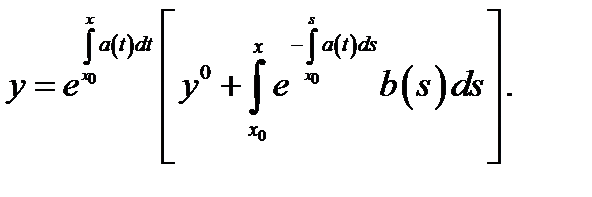
Доказательство. Найдем решение уравнения (1). Применим для этого так называемый метод вариации произвольной постоянной Лагранжа, который состоит в следующем.

Решим сначала однородное уравнение, соответствующее уравнению (1):

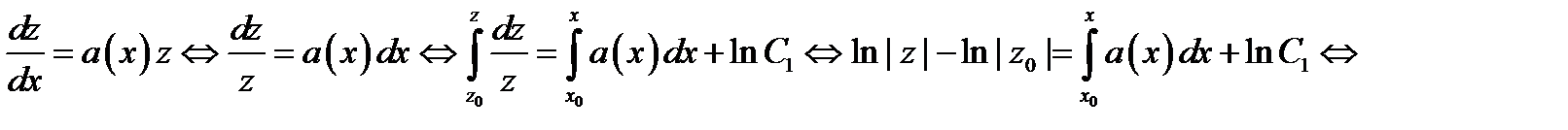
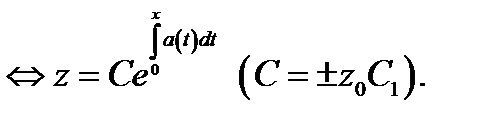Затем вычислим решение уравнения (1), варьируя постоянную в решении однородного уравнения, т.е. будем определять решение уравнения (1) в ви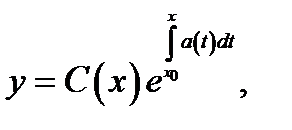де где 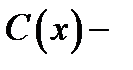неизвестная функция. Подставляя предполагаемое решение в уравнение (1), будем иметь

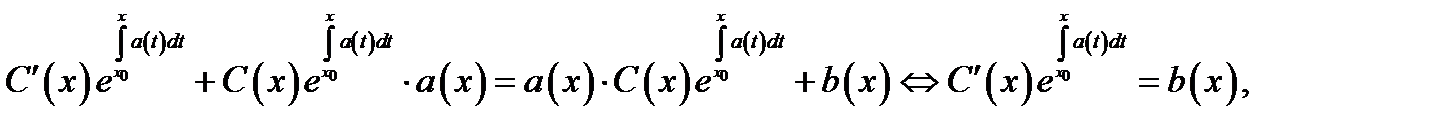
откуда находим 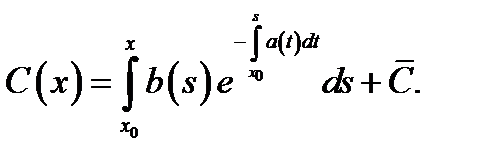Значит, общее решение уравнения (1) можно записать в виде

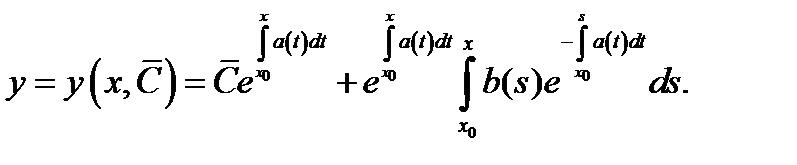
Подчиняя его начальному условию 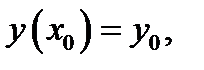найдём, что Следовательно, решение уравнения (1) с начальным условием 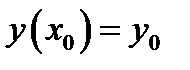имеет вид (2). Теорема доказана.

Замечание 1. Так как второе слагаемое в 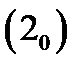есть частное решение (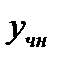) неоднород-

ного уравнения (1) (проверьте это!), а первое слагаемое суть общее решение соответствующего однородного уравнения, то для линейных дифференциальных уравнений имеет место утверждение: общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения, т.е.

Замечание 2. В отличие от нелинейных уравнений, имеющих, как правило, локальные решения, линейные дифференциальные уравнения имеют “глобальные решения,” т.е. они существуют на отрезке 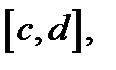на котором непрерывны коэффициенты уравнения (1).

И наконец, отметим, что так называемое уравнение Бернулли:

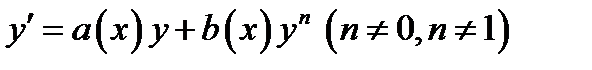
приводится к линейному уравнению делением обеих частей на 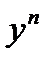и дальнейшей заменой переменной

Пример 1 (Кузнецов Л.А. Типовые расчеты). Решить задачу Коши

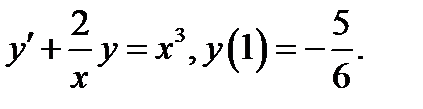
Решение. Можно было бы сразу воспользоваться формулой (6), но мы ещё раз продемонстрируем метод Лагранжа. Найдём сначала общее решение соответствующего однородного уравнения:

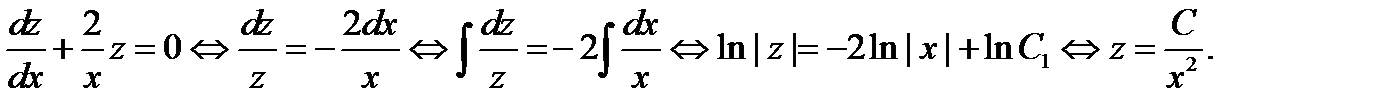
Вычисляя общее решение исходного уравнения в виде , будем иметь

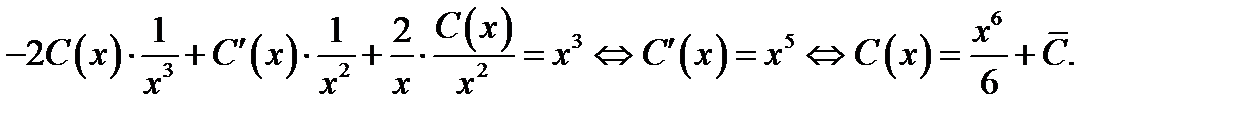
Значит, общим решением данного неоднородного уравнения является функция

Подчиняя её начальному условию 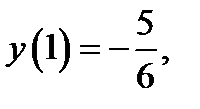будем иметь 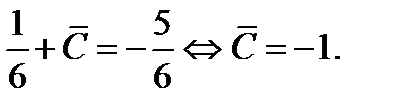Следовательно, решением исходной задачи Коши будет функция

Если в уравнении 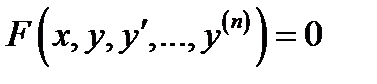порядок 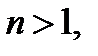то это уравнение называют уравнением высшего порядка. Мы будем рассматривать уравнения высших порядков, разрешённые относительно старшей производной:

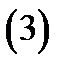
Областью определения уравнения (1) называется множество

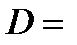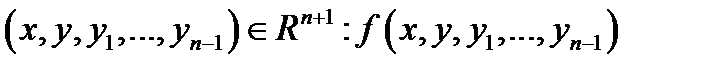{ имеет смысл }.

Дата добавления: 2014-11-29