Уравнения, допускающие понижение порядка

Задача Коши. Теорема существования и единственности решения задачи Коши. Общее решение и общий интеграл

Сначала дадим понятие решения уравнения (3).

Определение 1. Решением уравнения (3) на отрезке 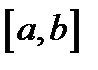называется такая функция

которая удовлетворяет следующим условиям:

1) функция 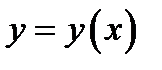дифференцируема 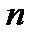раз на указанном отрезке;

2) точка 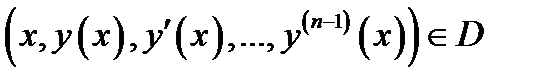при всех

3) имеет место тождество

Например, функция является решением уравнения 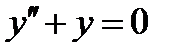на всей оси 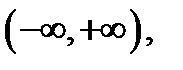так как имеет место тождество

Начальная задача (задача Коши) для уравнения (1) ставится следующим образом:

и формулируется так: для фиксированной начальной точки 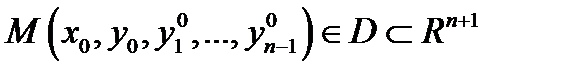найти решение 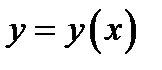уравнения (3), график которого (интегральная кривая) проходит через точку Имеет место следующее утверждение.

Теорема Коши (существования и единственности решения начальной задачи для уравнения высшего порядка). Пусть в уравнении (3) функция и её частные производные 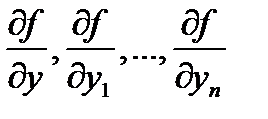непрерывны в области Тогда какова бы ни была начальная точка 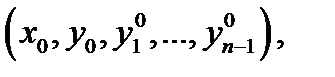лежащая внутри области 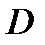, существует число 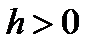такое, что задача Коши (4) с указанной начальной точкой имеет на отрезке решение 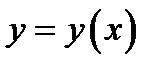и это решение единственно на указанном отрезке.

Обращаем внимание на достаточный и локальный характер этой теоремы (см. предыдущую лекцию). Так же, как и в случае уравнения первого порядка, здесь вводятся понятия частного и общего решений (и их интегралов).

Определение 2. Частным решением уравнения (3) называется решение какой-нибудь его задачи Коши (4). Общим решением уравнения (3) в области называется функция зависящая от 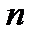произвольных постоянных 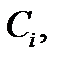удовлетворяю-

щая следующим условиям:

1) при любых допустимых значениях постоянных 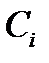функция является решением уравнения (1) на некотором отрезке

2) какова бы ни была начальная точка 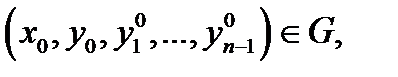существуют значения постоянных 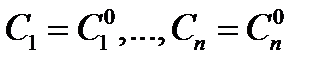такие, что функция 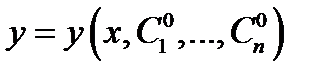является решением задачи Коши (4) с этой начальной точкой.

И, наконец, частный интеграл уравнения (3) есть частное решение этого уравнения, записанное в неявной форме а общий интеграл суть общее уравнения (3), записанное в неявной форме

Для проверки того, что соотношение 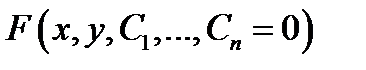является общим интегралом уравнения (3) надо из системы уравнений

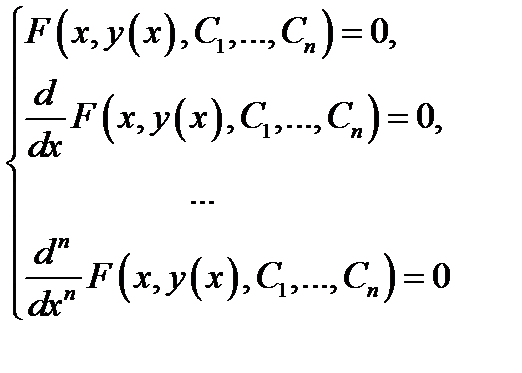
исключить произвольные постоянные 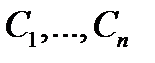. Если при этом будет получено дифференциальное уравнение (3) (или эквивалентное ему уравнение), то общий интеграл этого уравнения. Предлагаем в качестве упражнения проверить, что соотношение 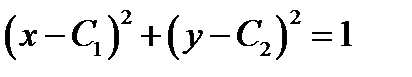является общим интегралом уравнения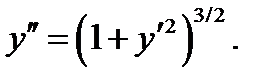

Ясно, что чем меньше порядок дифференциального уравнения, тем легче его решить. Посмотрим, какие уравнения допускают понижение порядка. Сначала рассмотрим простейшее уравнение

не содержащее в правой части неизвестную функцию. Оно легко решается последовательным интегрированием:

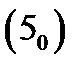
где 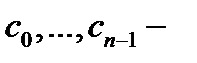произвольные постоянные. Нетрудно доказать так называемую формулу Коши для мерного повторного интеграла:

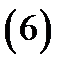
и, стало быть, записать решение (5) с помощью одномерного интеграла.

а) Уравнение, в котором отсутствуют неизвестная функция и её производные до порядка включительн о:

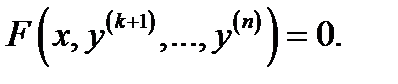
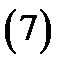
Порядок уравнения (7) понизится на 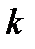единиц, если ввести новую функцию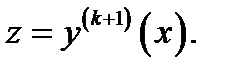

Действительно, после этой замены получим уравнение Если это

уравнение имеет общее решение 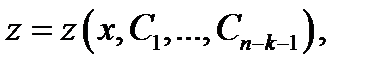то для решения исходного уравнения (7) надо проинтегрировать уравнение 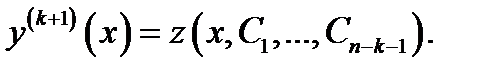Это уравнение типа (4). Его решение вычисляется последовательным интегрированием.

б) Уравнение, в котором отсутствует в правой части независимая переменная

Здесь для понижения порядка надо ввести новую неизвестную функцию Чтобы не усложнять выкладки, рассмотрим уравнение второго порядка

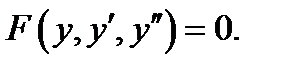
Сделав замену будем иметь (учесть, что ):

При этом уравнение (8) приобретает вид 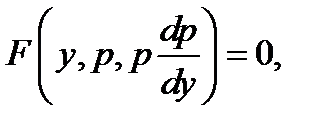т.е. является уравнением первого порядка. Найдя общее решение 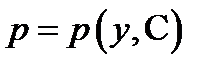этого уравнения, получим решение исходного уравнения (8), если проинтегрируем уравнение Рассмотрим примеры.

Пример 2 (Кузнецов Л.А. Типовые расчеты). Найти общее решение дифференциально-

го уравнения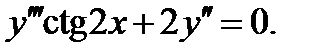

Решение. Так как в уравнении отсутствуют сама функция и ее производная, то делаем

замену 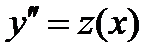. Тогда и уравнение приобретает вид

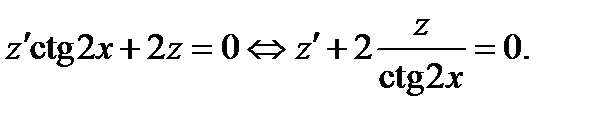
Получили линейное однородное уравнение первого порядка. Решаем его методом разделения переменных:

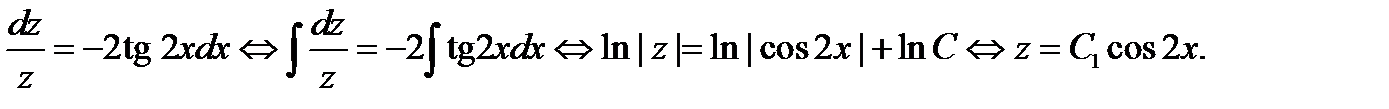
Теперь находим решение исходного уравнения:

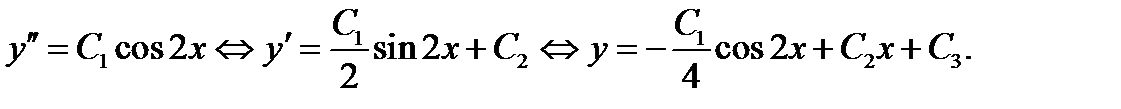
Пример 3 (Кузнецов Л.А. Типовые расчеты). Решить задачу Коши

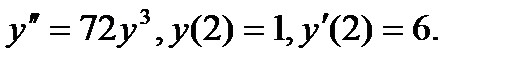
Решение. Так как в уравнении отсутствует независимая переменная то делаем замену замену Будем иметь (учесть, что ):

Исходное уравнение преобразуется к виду Начальное условие для функции

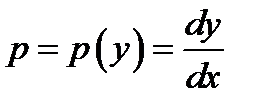находим, полагая в этом равенстве Тогда

Итак, надо решить задачу Разделяя переменные, получим

Учитывая, что в окрестности точки функция 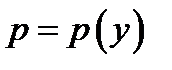положительна, будем иметь

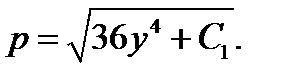Полагая в этом равенстве и учитывая, что , получаем, что

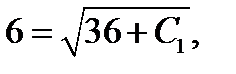т.е. 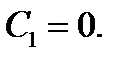Значит,

Полагая в этом равенстве и учитывая, что найдём, что Следовате-

льно, Это и есть ответ.

Лекция 3. Линейные дифференциальные уравнения высшего порядка. Однородные уравнения. Пространство решений, его размерность и базис (фундаментальная система решений). Структура общего решения.

Определитель Вронского. Условия линейной независимости решений однородного линейного дифференциального уравнения

Линейным дифференциальным уравнением -го порядка называется уравнение

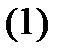
в котором неизвестная функция 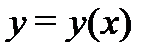и все ее производные входят линейным образом (т.е. с целой неотрицательной степенью не выше первой). При этом функции называются коэффициентами уравнения (1), а правая часть – неоднородностью этого уравнения. Если в (1) отсутствует неоднородность то уравнение (1) называется однородным. Если же 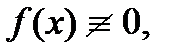то уравнение (1) называется неоднородным дифференциальным уравнением.

Уравнение (1) можно записать кратко 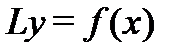, если обозначить через 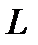–дифференциальный оператор --гo порядка:

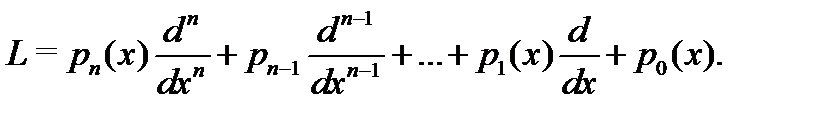
Дата добавления: 2014-11-29