Темы рефератов 1 страница

ТЕХНИЧЕСКИЕ СРЕДСТВА АВТОМАТИЗАЦИИ

.

Рис.1.7. Преобразованная структурная схема

Звенья W1(p) и W¢(p) согласно рис.1.7 включены параллельно. Таким образом, получили параллельное соединение двух инерционных звеньев. Частотная передаточная функция такого соединения равна сумме частотных передаточных функций звеньев, входящих в него. При этом сложение комплексов требует представления их в виде вещественной и мнимой частей.

Если W(j w )=U( w )+jV( w ), то, соответственно

S W(j w )= S U( w )+j S V( w ) (1.7)

W1(j w ) ;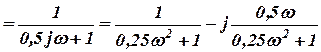

;

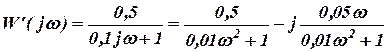Согласно (1.7)

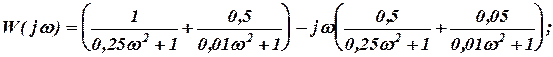
Таким образом, для заданного соединения звеньев

U( w )=

V( w )= (1.8)

Представляя в выражении (1.8) значения w от 0 до ¥, находим U( w ) и V( w ). По полученным значениям строим АФЧХ, как это показано в примере 1.1.

Можно также построить АФЧХ соединения звеньев путем суммирования векторов АФЧХ для одинаковых частот.

Пример 1.3. Построить АФЧХ соединения звеньев (рис.1.4), если W1(p) = 3/(0.2р+1);W2(p) = 2/р; W3(p)=0,5.

Решение. После преобразования схемы получим схему, приведенную на рис.1.7 (см. предыдущий пример), где

W1(p) = 3/(0.2p+1);W'(p)=2/(p+1).

найдем значения U( w ), U'( w ),V( w ) и V'( w ) и занесем их в табл.1.4. Просуммировав графически векторы АФЧХ, получим результирующую характеристику, соответствующую суммарным значениям U( w ) и V( w ) (рис.1.8).

Таблица 1.4

Параметр	Значения частоты
		0.5	1.0	2.0	5.0		¥
U( w )	3.0	2.97	2.88	2.59	1.5	0.6
V( w )		-0.3	-0.58	-1.03	-1.5	-1.2
U'( w )	2.0	1.6	1.0	0.4	0.08	0.02
V'( w )		-0.8	-1.0	-0.8	-0.38	-0.2
S U( w )	5.0	4.57	3.88	2.99	1.58	0.62
S V( w )		-1.10	-1.58	-1.83	-1.68	-1.4

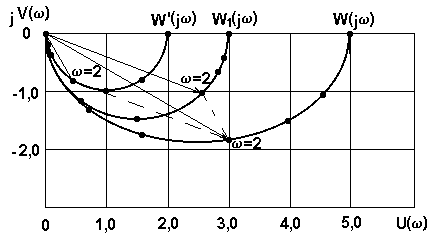
Рис.1.8. АФЧХ (к примеру 1.3)

Варианты 1.21...1.30. По функциональной схеме (рис.1.9) следящей системы управления приводом барабана летучих ножниц составить структурную схему и проверить систему на устойчивость по критерию Гурвица или Михайлова. Двигатель совместно с системой управления описывается дифференциальным уравнением

Передаточная функция тахогенератора с фильтром

w - частота вращения, рад/с;

T1, T2, T3 - постоянные времени, с;

kд - коэффициент передачи двигателя, рад/с.В;

kтг - коэффициент передачи тахогенератора, с.В/рад.

Значения указанных параметров для различных вариантов приведены в табл.1.5.

Литература: /1/, с.117-129.

Рис.1.9. Функциональная схема следящей системы:

1- прокатная клеть; 2- барабан; ТГ1, ТГ2- тахогенераторы;

Д - двигатель; СУ- система управления приводом

Таблица 1.5

Вариант	Значение параметров
	T1, с	T2, с	kд, рад/с.в	kтг с.в/рад.	T3, с
1.21	0.1	0.2			0,01
1.22	0.5	0.2			0.01
1.23	0.4	0.1			0.02
1.24	0.2	0.1			0.02
1.25	0.3	0.2	0.5		0.01
1.26	0.1	0.2			0.005
1.27	0.5	0.25			0.01
1.28	0.1	0.2			0.005
1.29	0.2	0.1			0.01
1.30	0.5	0.2			0.01

Варианты 1.31...1.40. Из условия устойчивости определить предельный (критический) коэффициент усиления электромеханической системы автомати­че­ского регулирования. Передаточные функции системы в разомкнутом состоянии и ее параметры приведены в табл.1.6.

Литература:/1/,с.117-129.

Таблица 1.6

Вариант	Передаточная функция	Значение параметров
		Т1, с	Т2, с	Т3, с
1.31		0.1	0.2	-
1.32	W(p)=k/p(T1p+1)(T2p+1)	0.2	0.2	-
1.33		0.3	0.4	-
1.34		0.1	0.2	0.3
1.35	W(p)=k/(T1p+1)(T2p+1)(T3p+1)	0.2	0.2	0.3
1.36		0.2	0.3	0.4
1.37		0.1	0.2	-
1.38	W(p)=k/p(T12p2+T2p+1)	0.5	0.2	-
1.39		0.4	0.1	-
1.40		0.5	0.25	-

Варианты 1.41...1.50. По функциональной схеме регулятора положения нажимных винтов прокатной клети (рис.1.10) составить структурную схему и проверить систему на устойчивость по критерию Михайлова. Передаточная функция датчика положения Wдп(p)=kдп. Передаточная функция предварительного усилителя (У) совместно с передаточной функцией тиристорного преобразователя (ТП) Wтп(p)=kтп/(T1p+1), а передаточная функция двигателя Wдв(p)=kдв/(T22p2+2 x T2p+1), где x -коэффициент демпфирования. Передаточный коэффициент редуктора kр=1/i, где i -передаточное число редуктора. Выходной сигнал - угол поворота нажимного винта f. Значения параметров - в табл.1.7.

Литература: /1/, с.82-85; 117-129.

Краткие сведения из теории

Одним из основных условий работоспособности АСР является ее устойчивость, т.е. способность системы возвращаться в исходное состояние после снятия воздействия, выведшего ее из этого состояния.

Необходимым и достаточным условием устойчивости системы является отрицательность вещественной части комплексных корней характеристического уравнения. Характеристическое уравнение получают обычно, приравнивая к нулю дифференциальный оператор при выходной величине в исходном дифференциальном уравнении.

Рис.1.10. Функциональная схема регулятора положения

нажимных винтов: У - предварительный усилитель;

ТП - тиристорный преобразователь; Д - двигатель;

ДП - датчик положения нажимных винтов

Таблица 1.7

Вариант	Значения параметров
	kдп, В/рад	kтп	T1, с	T2, с	x	kдв, рад/с В	i
1.41			0.01	0.1	1.0
1.42			0.01	0.2	1.0
1.43			0.03	0.1	1.2
1.44			0.01	0.5	1.2
1.45			0.01	0.2	1.2
1.46			0.02	0.5	1.3
1.47			0.02	0.1	1.3
1.48			0.03	0.2	1.2
1.49			0.03	0.2	0.8
1.50	0.5		0.02	0.2	0.8

Вычисление корней весьма просто лишь для характерестического уравнения первой и второй степени. Существуют общие выражения для корней уравнений третьей и четвертой степени, но эти выражения громоздки и практически не применяются. Для уравнений более высоких степеней вообще невозможно написать общие выражения для корней через коэффициенты характерестического уравнения.

Существуют правила, позволяющие определять устойчивость системы без вычисления корней. Эти правила называют критериями устойчивости. Существует несколько критериев устойчивости. Все они математически эквивалентны, так как решают вопрос о знаке вещественной части корней характерестического уравнения. Их разделяют на алгебраические и частотные.

Алгебраические критерии позволяют судить об устойчивости системы по коэффициентам многочлена

D(p)=anpn+an-1pn-1+...+a1p+a0 (1.9)

Во-первых, необходимым (но, недостаточным!) условием устойчивости является положительность всех коэффициентов an,...,a0. Если хотя бы один из коэффициентов меньше нуля, то система неустойчива и дальнейшее исследование не имеет смысла. Если an>0, an-1>0,..., a0>0, то согласно алгебраическому критерию устойчивости Гурвица система устойчива, если все определители Гурвица больше нуля. Для коэффициентов многочлена (1.9) составляют квадратную матрицу n ´ n, по главной диагонали которой записывают все коэффициенты от an-1 до a0 и далее заполняют ее, как показано ниже. В случае отсутствия данного коэффициента и если его номер больше n или меньше нуля, на его место проставляют нуль. В главной диагонали определителя оказываются последовательно все коэффициенты, кроме an.

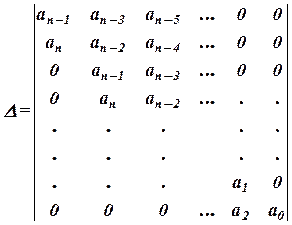
Определители Гурвица составляют так:

D 1=an-1>0;

и т.д.

Последний определитель включает всю матрицу. Но каждый последующий определитель может быть вычислен через предыдущий. Так как в устойчивой системе D n-1>0, то положительность последнего определителя обеспечивается, если a0>0.

Рассмотрим критерий Гурвица для нескольких конкретных значений n.

Для n=1

D(p)=a1p+a0,

и условие устойчивости сводится к неравенствам

a1>0; a0>0.

Для n=2

D(p)=a2p2+a1p+a0,

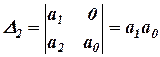
Условие устойчивости:

a2>0;a1>0; a0>0.

Например, звено с передаточной функцией k/(T22p2+T1p+1) устойчиво, если перед всеми членами в знаменателе стоит знак плюс.

Если n=3, то

D(p)=a3p3+a2p2+a1p+a0,

В этом случае условия устойчивости:

a3>0;a2>0;

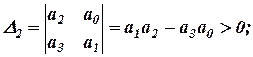
D 3 = a0 D 2>0.

Если D 2>0, то a0>0. Т.о. условие устойчивости сводится к положительности всех коэффициентов и предпоследнего минора D 2. Критическое значение коэффициента усиления может быть найдено из выражения

a2a1=a3a0,

где a0 включает предельный коэффициент усиления kпр (см. пример 1.5).

Для n=4

D(p)=a4p4+a3p3+a2p2+a1p+a0,

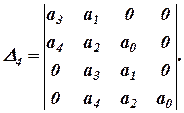
Условия устойчивости:

a4>0;a3>0; D 2 = a3a2-a4a1>0;

D 3 = a1 D 2-a32a0>0; D 4 = a0 D 3>0.

Таким образом, условия устойчивости опять сводятся к требованию положительности всех коэффициентов и предпоследнего минора D 3. (Условие D 2>0 при этом вытекает из неравенства D 3>0 с учетом того, что D 4>0).

В общем случае системы n-го порядка необходимым условием устойчивости является требование положительности всех коэффициентов. Анализ устойчивости надо начинать с проверки этого простого условия. Если оно не выполняется, то отпадает необходимость в составлении и проверке остальных неравенств.

Для характеристических уравнений невысоких порядков применение алгебраических критериев достаточно просто. Если же уравнение имеет высокий порядок, то применить алгебраические критерии затруднительно. Если система включает звено запаздывания, то характеристическое уравнение становится трансцендентным из-за члена e-p t.

В подобных случаях используют частотные критерии. Они удобны в силу простоты геометрической интерпретации и наглядности.

Согласно критерию Михайлова для устойчивости системы необходимо и достаточно, чтобы с ростом w от 0 до ¥ годограф Михайлова, начинаясь на положительной части действительной оси, обходил последовательно n квадрантов, где n - порядок характеристического полинома

D(p)=anpn+an-1pn-1+...+a0.

На рис.1.11 показаны кривые Михайлова для устойчивых систем различных порядков.

Рис.1.11. Кривые Михайлова для устойчивых систем

Пример 1.4. Система описывается дифференциальным уравнением

где х, у - соответственно входная и выходная величины;

T1=0,02 c; T2=0,5 c; T3=0,2 c - постоянные времени; k=5 - коэффициент усиления. Проверить систему на устойчивость по критерию Гурвица.

Решение. Запишем передаточную функцию разомкнутой системы, соответствующую заданному дифференциальному уравнению:

(1.10)

Характеристический многочлен замкнутой системы

D(p)=a3p3+a2p2+a1p+a0,

где: a3=T33; a2=T22; a1=T1; a0=k+1, т.е.

a3=0,008; a2=0,25; a1=0,2; a0=6.

D 2=a2a1-a3a0=0,050-0,048>0.

Условия устойчивости a3>0, a2>0, a1>0, a0>0 и D 2>0 выполняются.

Таким образом, система с передаточной функцией (1.10) устойчива, если при положительности всех коэффициентов произведение a2a1 больше произведения a3a0.

Для того, чтобы повысить точность статической системы регулирования, т.е. снизить статическую ошибку, необходимо увеличить коэффициент передачи системы. Однако, для существенного уменьшения статического отклонения при этом требуется увеличить коэффициент передачи до очень больших величин. Технически это реализовать возможно, однако на величину коэффициента усиления накладывается ограничение по условию устойчивости. В связи с этим определение предельного коэффициента усиления имеет важное практическое значение. Определение предельного коэффициента усиления равносильно определению условия нахождения системы на границе устойчивости.

Для того, чтобы найти предельный коэффициент усиления, необходимо выполнить анализ характеристического уравнения.

Пример 1.5. Пусть задана передаточная функция разомкнутой системы

W(p)=k/(T1p+1)(T2p+1)(T3p+1).

В этом случае

D(p)=(T1p+1)(T2p+1)(T3p+1)+k, (1.11)

что соответствует замкнутой системе регулирования, содержащей три инерционных звена с общим коэффициентом усиления k. Необходимо определить предельное значение kпр, при котором система перестает быть устойчивой.

Решение. Перепишем (1.11) в виде

D(p)=T1T2T3p3+(T1T2+T1T3+T2T3)p2+(T1+T2+T3)p+1+k,

или

D(p)=a3p3+a2p2+a1p+a0,

где a3=T1T2T3; a2=T1T2+T1T3+T2T3; a1=T1+T2+T3;a0=1+k.

Согласно критерию Гурвица система устойчива, если выполняются неравенства

а3>0, D 1=a2>0, D 2=a2a1-a3a0>0; D 3=a0 D 2>0,

т.е. если, при условии положительности всех коэффициентов, выполняется неравенство

a2a1>a3(1+k), где (1+k)=a0. (1.12)

Неравенство (1.12) можно переписать в виде

k<a2a1/a3- 1.

Это неравенство нарушится при

k ³ kпр=a2a1/a3- 1. (1.13)

Пусть, например, T1=0,2 с ; T2=0,1 с ; T3=0,5 с.

Тогда

a3=T1T2T3=0,2•0,1•0,5=0,01;

a2=T1T2+T1T3+T2T3=0,2•0,1+0,2•0,5+0,1•0,5=0,17;

a1=T1+T2+T3=0,2+0,1+0,5=0,8.

Согласно (1.13)

kпр=a2a1/a3- 1=0,17•0,8/0,01-1=12,6.

Пример 1.6. Характеристический многочлен замкнутой системы такой же, как и в предыдущем примере. Определить предельный коэффициент усиления, применив критерий устойчивости Михайлова.

Решение. Представим (1.11) в виде

D(p)=(T1p+1)(T2p+1)(T3p+1)+k=A(p)+k.

Для решения задачи следует построить годограф Михайлова

D(j w )=A(j w )+k.

Для этого вначале построим годограф

A(j w )=(T1j w +1)(T2j w +1)(T3j w +1). (1.14)

Преобразуем (1.14) к виду A(j w )=U( w )+jV( w ), где

U( w )=1-a2 w 2;

V( w )= w(a1-a3 w 2).

Подставив значения из предыдущего примера, получим

(1.15)

Задаваясь значениями w в диапазоне от 0 до ¥, рассчитываем значения U( w ) и V( w ). Результаты расчета сводим в табл. 1.8.

Таблица 1.8.

w,с-1		1,0	2,0	3,0	4,0	5,0	6,0	8,94	20,0	¥
U( w )		0,83	0,32	-0,53	-1,72	-3,25	-5,12	-12,6	-67	-¥
V( w )	0	0,79	1,52	2,13	2,56	2,75	2,64		-64	-¥

При частоте w =8,94, как следует из (1.15), V( w ) =0, т.е. годограф пересекает действительную ось.

Годограф A(j w ) показан на рис. 1.12.

Для того, чтобы получить годограф D(j w ), достаточно мнимую ось сместить влево на величину k. Из рис.1.12 следует, что система находится на границе устойчивости, если значение равно значению kпр, при котором годограф D(j w ) пройдет через начало координат. Cогласно рис.1.12 величина kпр =12,6, что совпадает с результатом предыдущей задачи.

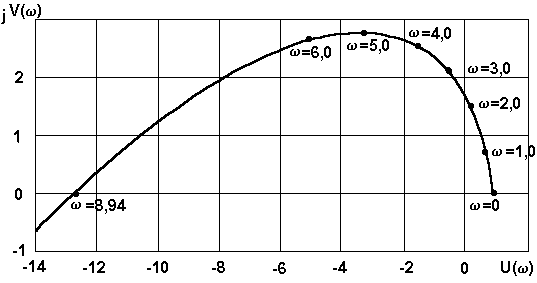
Рис.1.12. К определению предельного коэффициента усиления

Варианты 1.51…1.75. Выбрать простейший регулятор, обеспечивающий поддержание заданных параметров переходного процесса, и определить его настройки для стабилизации температуры в сварочной зоне методической нагревательной печи, имеющей запаздывание t_об, постоянную времени Т_об, коэффициент передачи k_oá и максимальное возмущающее воздействие x_вх. Технологические требования: допустимая статическая ошибка не должна превышать Dx_ст^доп;максимальноединамическое отклонение - x₁^доп; допустимое время регулирования - t_р^доп в соответствии с заданным типовым законом (табл. 1.9). Проверку соответствия качества системы заданным требованиям выполнить на ПЭВМ с использованием прикладного пакета моделирования.

Табл. 1.9.

№ вар	Dxст^доп,°С	x1^доп,°С	tр^доп, с	tоб, с	Тоб, с	koá,°С /% хода РО	xвх, % хода РО	Типовой закон
1.51						2.8		20% перерег.
1.52						2.5		апериодич.
1.53						2.6		min òx^2dt
1.54						2.7		20% перерег.
1.55						2.8		апериодич.
1.56						2.9		min òx^2dt
1.57						2.5		20% перерег.
1.58						3.1		апериодич.
1.59						2.8		min òx^2dt
1.60						2.8		20% перерег.
1.61						2.5		апериодич.
1.62						2.6		min òx^2dt
1.63						2.7		20% перерег.
1.64						2.8		апериодич.
1.65						2.9		min òx^2dt
1.66						2.4		20% перерег.
1.67						3.1		апериодич.
1.68						2.6		min òx^2dt
1.69						2.6		20% перерег.
1.70						2.5		апериодич.
1.71						2.6		min òx^2dt
1.72						2.7		20% перерег.
1.73						2.8		апериодич.
1.74						2.9		min òx^2dt
1.75						2.5		20% перерег.

Краткие сведения из теории

Автоматический регулятор - это комплекс устройств, подключаемых к объекту регулирования и обеспечивающих автоматическое поддержание заданных значений его регулируемых величин или автоматическое изменение их по определенному закону.

Определяющим условием при выборе регулятора и расчета его настроек является качество регулирования, определяющее точность поддержания технологического режима и ее экономическую эффективность. При этом под выбором регулятора понимают выбор закона регулирования.

Закон регулирования - это математическая зависимость между входной и выходной величинами регулятора.

Дата добавления: 2014-12-16