Закон сохранения импульса системы

Теорема об изменении импульса системы.

Рассмотрим вначале систему, состоящую из n материальных точек, каждая из которых взаимодействует с любой другой. Кроме того, на материальные точки системы могут действовать материальные точки, не входящие в данную систему. Поэтому все силы, действующие на материальные точки механической системы, разделяют на внешние 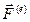(external) и внутренние 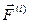силы (internal).

Внешними называют силы, действующие на элементы системы со стороны элементов, не входящих в эту систему. Внутренними называют силы взаимодействие элементов системы между собой. Запишем для каждой материальной точки механической системы основной закон динамики: 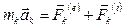, k =1, 2, 3…, n, где 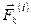– равнодействующая внутренних сил, действующих на k -ую материальную точку; 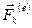– равнодействующая всех внешних сил, действующих на k -ую материальную точку.

Просуммируем полученные уравнения: 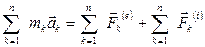. Ясно, что на основании III аксиомы динамики материальной точки: , где 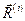– главный вектор внутренних сил. Величину 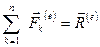называют главным вектором внешних сил. Так как массы материальных точек есть величины постоянные, то 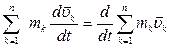. Сумму импульсов всех материальных точек системы называют импульсом механической системы материальных точек: 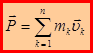. Используя полученные уравнения, запишем: 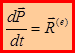. Данная формула выражает математическую запись теоремы об изменении импульса механической системы материальной точки: первая производная по времени от импульса механической системы материальных точек равна главному вектору внешних сил.

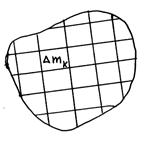
В случае материального тела мы мысленно разбиваем его на элементы, которые заменяем материальными точками при стремлении объемов элементов к нулю (или стремлении числа элементов к бесконечности): 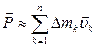. Устремим , , где 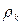– плотность k -го элемента. Используя определение интеграла, запишем выражение для импульса материального тела: 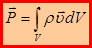. Поступая аналогично предыдущему, получим выражение для главного вектора внешних сил, действующих на материальное тело: 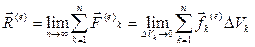. Или: 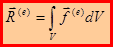. Теорема об изменении импульса материального тела: 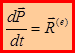. Если рассматривать систему, состоящую из N материальных тел, то теорема об изменении импульса для такой системы имеет такое же выражение, но под импульсом системы и главным вектором внешних сил понимают: , .

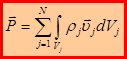В декартовой системе координат: 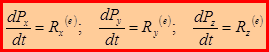. Если главный вектор внешних сил равен нулю, то механическая система называется замкнутой. Из теоремы об изменении импульса системы следует, что если механическая система является замкнутой (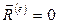), то ее импульс сохраняется (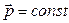). В этом заключается закон сохранения импульса механической системы. В случае, когда главный вектор внешних сил не равен нулю, но его проекция на какую-либо ось координат равна нулю, то сохраняется соответствующая проекция импульса механической системы.

Дата добавления: 2014-11-29