Закон сохранения полной механической энергии системы

Теорема об изменении кинетической энергии системы.

Запишем основной закон динамики для каждой точки: 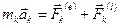, k = 1, 2, 3,…, n. Умножим скалярно это уравнение на 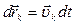(учтено ):

, .

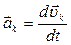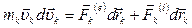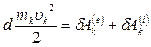Здесь 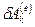– элементарная работа внешних сил по перемещению k -ой материальной точки, 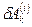– элементарная работа внутренних сил по перемещению k -ой материальной точки.

Проинтегрируем записанное уравнение по времени: .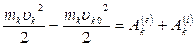

Просуммируем полученные уравнения: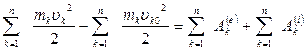

Здесь 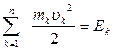– кинетическая энергия системы материальных точек:

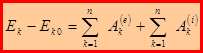– теорема об изменении кинетической энергии системы материальных точек: изменение кинетической энергии системы материальных точек равно сумме работ всех внешних и внутренних сил, действующих на элементы системы.

Эта теорема справедлива для материального тела и для системы материальных тел.

Под кинетической энергией материального тела понимаем: .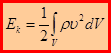

Под кинетической энергией системы материальных тел понимаем: 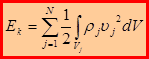. В случае, когда все внутренние силы системы являются консервативными: 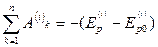. Тогда: 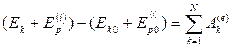. Если также и внешние силы консервативны: 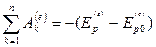, то: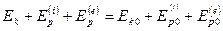

Величина 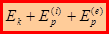– полная механическая энергия системы.

– закон сохранения полной механической энергии системы: если все внутренние и внешние силы, действующие на элементы системы консервативны, то ее полная механическая энергия сохраняется.

Если только часть сил, действующих на элементы системы консервативны, то полная механическая энергия не сохраняется. Она может убывать или возрастать.

Дата добавления: 2014-11-29