Основное уравнение динамики вращательного движения

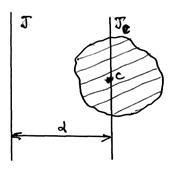
Момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс тела и произведения массы тела m на квадрат расстояния между осями.

Кинетическая энергия твёрдого тела при произвольном движении равна сумме кинетической энергии поступательного движения со скоростью центра масс и кинетической энергии вращения вокруг мгновенной оси, проходящей вокруг центра масс.

МОМЕНТЫ ИНЕРЦИИ ТВЁРДЫХ ТЕЛ

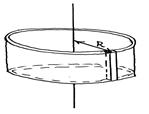Момент инерции твёрдого 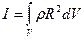тела есть характеристика самого тела вне зависимости от его вращения. Величины 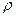и R есть функции координат; интегрирование осуществляется по всему объёму. В общем случае неоднородного ( 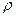≠ const) тела произвольной формы вычисление момента инерции является очень сложной задачей. В качестве примеров рассмотрим нахождение моментов инерции некоторых однородных ( 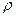= const) тел правильной формы.

1) Момент инерции тонкостенного однородного цилиндра массы m и радиусом R относительно его оси симметрии:

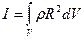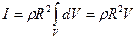, . С учетом ,

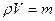получаем

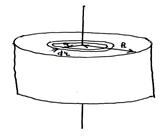2) Момент инерции сплошного однородного цилиндра массы m радиусом R и высотой H относительно его оси симметрии: . Разобьем цилиндр на бесконечно тонкие слои:

.

С учётом 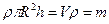, получаем:

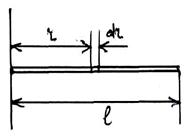3) Момент инерции тонкого однородного стержня массы m длиной ℓ относительно оси проходящей через его конец перпендикулярно его оси: . .

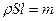С учётом , получаем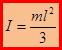

4) Момент инерции однородного шара массы m радиусом R относительно оси, проходящей через его середину. Приведём конечный результат без вывода: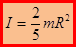

Теорема Штейнера

В случае, когда момент инерции необходимо найти относительно произвольной оси задача существенно упрощается, если для её решения воспользоваться теоремой Штейнера.

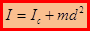
Пример: в соответствии с теоремой Штейнера найдем момент инерции 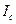тонкого однородного стержня относительно оси, проходящей через центр масс, если известен момент инерции относительно оси, проходящей через конец стержня. Учтём, что : 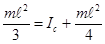. Получим: .

Работа внутренних сил абсолютно твёрдого тела (АТТ)

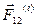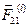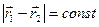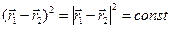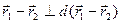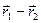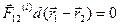Найдём элементарные работы внутренних сил, с которыми действуют друг на друга две точки АТТ и : Для АТТ , , . Поэтому: . Но сонаправлен с . Таким образом . Следовательно: . Поэтому 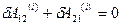– работа внутренних сил АТТ равна нулю.

Закон сохранения полной механической энергии для абсолютно твердого тела: полная механическая энергия абсолютно твердого тела сохраняется, если все внешние силы являются консервативными.

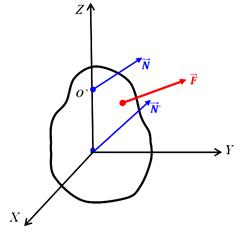Пусть твёрдое тело вращается вокруг неподвижной оси, совпадающей с осью 0Z. На тело действует активная сила 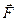, которая известна и силы реакци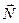и и 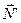. Нас интересует, как в этом случае изменяется со временем угол ?

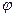Запишем теорему о движении центра масс и теорему об изменении кинетического момента АТТ:

;

.

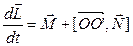Момент силы 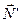равен нулю.

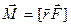– момент активной силы.

Система координат XYZ – неподвижна.

Во втором уравнени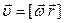и: . или

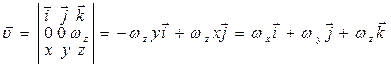; То есть ; ; .

.

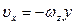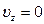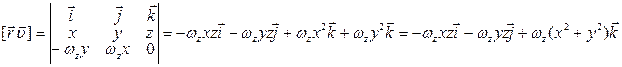Учитывая это запишем выражение для проекции вектора :

, , .

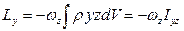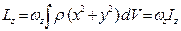В формулах величины 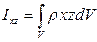и 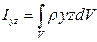называют центробежными моментами инерции вращающегося твердого тела; 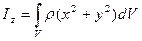– главный момент инерции твёрдого тела относительно оси 0Z.

Запишем начальные уравнения в проекциях:

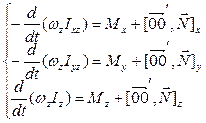
Т.к. твёрдое тело не может вращаться относительно осей 0X и 0Y, первые два уравнения системы выражают условия равновесия твёрдого тела относительно этих осей и могут служить для нахождения неизвестных сил реакции .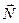

Моменты неизвестных сил реакци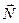и и 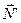относительно оси Z равны. Третье уравнение системы можно записать так: 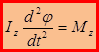; ; – основное уравнение динамики вращательного движения.

Решением этого дифференциального уравнения второго порядка относительно координаты φ твёрдого тела является кинематический закон движения твёрдого тела. Следовательно, это уравнение в динамике вращательного движения твёрдого тела имеет такое же значение, как и второй закон Ньютона в динамике материальной точки или теорема о движении центра масс в режиме поступательного движения.

Дата добавления: 2014-11-29