Дифференциальное уравнение неразрывности потока

Уравнение Бернулли для реальных жидкостей

При движении реальной жидкости её гидродинамический напор Н (или сумма потенциальной и кинетической энергии потока) не остаётся постоянным, так как частицы жидкости встречают сопротивление, вызванное силами вязкости и различными препятствиями (кранами, вентилями, поворотами и т. п.), приводящими к изменению сечения или направления потока. На преодоление этого сопротивления, которое принято называть гидравлическим, расходуется энергия движущейся жидкости, превращающаяся в тепло. Это тепло идёт на нагревание потока и рассеивается в окружающую среду. Поэтому во всяком последующем положении или сечении потока энергия частицы жидкости будет меньше, чем в предыдущем, т. е..

z₁ + p₁/ρg+ w ₁²/2g > z₂ + p₂/ρg+ w ₂²/2g.

При этом часть потенциальной энергии переходит в потерянный напор h_п. Очевидно, что для того, чтобы сохранить равенство напоров в любом сечении потока, необходимо в правую часть уравнения Бернулли добавить член, учитывающий потери напора:

z₁ + p₁/ρg+ w ₁²/2g = z₂ + p₂/ρg+ w ₂²/2g + h_п.(3.7)

Потерянный напор h_п включает в себя две составляющие – потери напора на трение h_тр и на преодоление так называемых местных сопротивлений h_{м.с .}, под которыми понимают источник изменения направления или сечения потока, т. е. h_п = h_тр + h_м.с

С помощью уравнения Бернулли можно определить необходимый напор (или давление) для того, чтобы жидкость с заданной скоростью транспортировалась по трубопроводу, а также скорость и расход жидкости, время истечения жидкости из отверстия в резервуаре.

Рассмотрим жидкость, текущую без пустот и разрывов и при отсутствии источников массы. Выделим в объёме жидкости элементарный параллепипед объёмом dV = dxdydz, рёбра которого ориентированы параллельно осям координат (рис. 5).

Левая грань: площадь грани dS = dydz, составляющая скорости потока вдоль оси х в точках, лежащих на левой грани, - w_x, массовый расход жидкости: M=wSρ.

Тогда через эту грань в параллепипед войдёт вдоль оси x за единицу времени масса жидкости ρw_xdydz, а за промежуток времени dτ - масса жидкости М_х = ρw_xdydzdτ

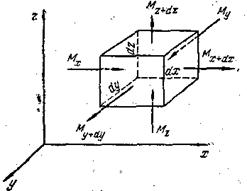
Рис. 5. К выводу дифференциального уравнения неразрывности потока

Правая грань: скорость (w_x + ( w_x/ x)dx);

плотность (ρ + ( ρ/ x)dx).

Тогда через правую грань за время dτ выйдет масса жидкости

М_{х + dx} = [ρw_x + ( (ρw_x)/ x)dx] dydzdτ.

Приращение массы жидкости в параллепипеде вдоль оси х

dM _x = M_x - М_{x+ dx} = - ( (ρw_x)/ x)dxdydzdτ. Аналогично: dM _y = - ( (ρw_y)/ y)dxdydzdτ, dM _z = - ( (ρw_z)/ z)dxdydzdτ

Общее накопление массы жидкости (dM) в параллепипеде за время dτ равно сумме её приращений вдоль всех осей координат:

dM = - ( (ρw_x)/ x + (ρw_y)/ y + (ρw_z)/ z) dxdydzdτ (3.8)

Вместе с тем изменение массы в полностью заполненном жидкостью объёме параллепипеда возможно только вследствие изменения плотности жидкости в этом объёме, то есть dM = ( ρ/ τ) dxdydzdτ (3.9).

Приравнивая оба выражения для dM (3.8) и (3.9), сокращая на (- dxdydz) и перенося ρ/ τ в левую часть уравнения, получим:

ρ/ τ + (ρw_x)/ x + (ρw_y)/ y + (ρw_z)/ z = 0 (3.10) –

это дифференциальные уравнения неразрывности потока для неустановившегося движения сжимаемой жидкости. В установившемся потоке плотность не изменяется во времени, т. е. ρ/ τ = 0 и уравнение (3.10) принимает вид:

δ(ρw_x)/δx + δ(ρw_y)/δy + δ(ρw_z)/δz = 0 (3.11).

Для капельных жидкостей ρ = const, поэтому

ρ( w_x / x + w_y/ y + w_z / z) = 0 (3.12),

ρ≠0, поэтому w_x / x + w_y/ y + w_z / z = 0 (3.13) - дифференциальное уравнение неразрывности потока несжимаемой жидкости.

Чтобы перейти ко всему объёму жидкости, проинтегрируем уравнение (3.11), принимая, что площадь сечения трубопровода переменна. Получаем ρ wS = const (3.14)- это уравнение неразрывности (сплошности) потока в интегральноц форме для установившегося движения. Для 3-х различных сечений трубопровода уравнение сплошности принимает вид: ρ₁w₁S₁ = ρ₂w₂S₂ = ρ₃w₃S₃ , М₁ = М₂ = М₃, т. е. при установившемся потоке, полностью заполняющем трубопровод, через каждое поперечное сечение проходит в единицу времени одна и та же масса жидкости. Поэтому уравнение (3.14) называют также уравнением постоянства расхода и оно является частным случаем закона сохранения массы и выражает материальный баланс потока. Для несжимаемых жидкостей ρ = const, поэтому уравнение (3.14) принимает вид: wS = const (3.15).

Дата добавления: 2014-12-16