Режимы движения жидкости

Рядом исследователей (Хеганом в 1869 г., Менделеевым в 1880 г., Рейнольдсом в 1883 г.) было замечено, что существует два принципиально разных режима движения жидкости. Наиболее полно этот вопрос был исследован Рейнольдсом с помощью очень простого прибора (рис. 7).

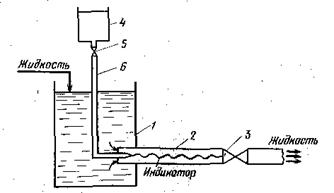
Рис. 6. Прибор Рейнольдса для изучения режимов движения жидкости: 1 - сосуд; 2 - стеклянная труба; 3, 5 -краны; 4 - напорная емкость; 6 - капиллярная трубка

Прибор состоял из сосуда 1, в котором для создания стационарного потока поддерживался постоянный уровень жидкости, и присоединённой к нему стеклянной горизонтальной трубы 2. в начале опыта слегка приоткрывали кран 3, и из сосуда начинала вытекать исследуемая жидкость. Затем в трубу 2 по её оси через капиллярную трубку 6 из напорной ёмкости 4 с помощью крана 5 подавали подкрашенную струйку жидкости, имеющую одинаковые с рабочей жидкостью плотность и скорость. При малых расходах рабочей жидкости тонкая окрашенная струйка продвигалась внутри трубы, не смешиваясь со всей массой жидкости, т.е. пути частиц рабочей и подкрашенной жидкости в этих условиях прямолинейны и движутся они по параллельным траекториям. Таким образом, подкрашенная струйка распространяется вдоль оси трубы невозмущенной. Такое установившееся течение было названо ламинарным.

При достаточно больших расходах (скоростях) жидкости пове­дение окрашенной струйки иное. Сначала струйка проходит некоторое расстояние в трубе 2, оставаясь невозмущен­ной, а затем она начинает приобретать волнообразное движение, колеблется из стороны в сторону и, наконец, полностью размы­вается, смешиваясь с основной массой рабочей жидкости. Это неупорядоченное движение с интенсивным перемешиванием по сечению потока принято называть турбулентным.

Экспериментально установлено, что переход от ламинарного режима к турбулентному зависит не только от скорости потока w, но и от физических свойств жидкости (вязкости μ и плотности ρ) и определяющего.

Скорость любого самопроизвольного процесса можно выразить как отношение движущей силы процесса к сопротивлению движения. Движение слоя жидкости происходит под действием разности давлений p₁ и p₂ с обеих торцевых сторон трубопровода, т. е. движущая сила ∆p = p₂ – p₁.

Оценим скорость движения слоя жидкости, непосредственно прилегающего к стенке трубы w_0-тр:

w_0-тр = ,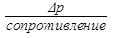

сопротивлением движению нулевого слоя является сопротивление стенки трубы R_тр, имеющее очень большую величину:

w_0-тр = 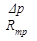, R_тр → 0, w_0-тр ≈ 0.

Оценим скорость движения первого слоя относительно нулевого. Сопротивлением движению этого слоя является вязкость жидкости μ, тогда:

w_1-0 = 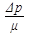= w ≠ 0, значит w_1-тр = w + 0 = w.

Аналогично скорость движения второго слоя относительно первого равна w_2-1 = (∆p/μ) = w, w_2-0 = w + w = 2w, w_2-тр = 2w + 0 = 2w.

w_3-2 =(∆p/μ) = w, w_3-тр = 2w + w = 3w, и так далее.

Таким образом, при ламинарном течении жидкости распределение скоростей по сечению потока параболическое. Как уже было сказано, в инженерных расчётах обычно используют среднюю скорость w_ср. В случае ламинарного течения её определяют следующим образом:

w_ср = .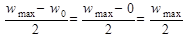

При турбулентном движении кривая распределения скоростей по сечению имеет отличный от параболы вид – вершина кривой значительно сглажена (рис.). При этом:

w_ср =w_max·f(Re).

Чем больше Re, тем ближе средняя скорость потока к максимальной.

Дата добавления: 2014-12-16