Материальный баланс. Рабочая линия

Рабочие концентрации распре­деляемого вещества не равны равновесным, и в действующих аппаратах никогда не достигают равновесных значений. Зависимость между рабочими концентрациями распределяемого ве­щества в фазах у = f (х) изображается линией, которая носит название рабочей линии. Вид функции у = f (х) или уравнение рабочей линии в его общем виде, является одинаковым для всех массообменных процессов и получается из их материальных балансов. Материальный баланс представляет собой вещественное выражение закона сохранения массы применительно к процессам химической технологии: масса веществ, поступивших на технологическую операцию (приход), равна массе веществ, полученных в этой операции (расход), что записывается в виде уравнения баланса.

Рассмотрим схему массообменного аппарата, работающего в режиме идеального вытеснения при противотоке фаз (рис. 27). Пусть в процессе массопередачи из фазы в фазу, например из газовой фазы в жидкую, переходит только один распределяемый компонент. Сверху в аппарат поступает L_н кг/сек жидкой фазы, содержащей х_н мас. долей распределяемого компонента, а снизу из аппарата удаляется L_к кг/сек той же фазы, содержащей х_к мас. долей распределяемого компонента. Снизу в аппарат поступает G_н кг/сек другой фазы (газовой) концентрацией у_н и сверху удаляется G_к этой фазы, имеющей концентрацию у_к мас. долей распределяемого компонента. Тогда материальный баланс по всему веществу G_н + L_н = G_к + L_к, и материальный баланс по распределяемому компоненту G_н у_н + L_н х_н = G_ку_к + L_кх_к.

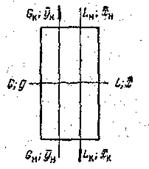
Рис. 27. К выводу уравнения материаль­ного баланса противоточного массообменного аппарата

Теперь напишем уравнения материального баланса для части аппарата от его нижнего конца до некоторого произвольного сечения, для которого расходы фаз составляют G и L кг/сек, а их текущие концентрации равны у и х соответственно.

По всему веществу G_н + L = G + L_к, по распределяемому компоненту G_н у_н + Lх = Gу + L_кх_к.

Решая это уравнение относительно у, получим:

у = 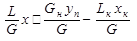(7.1).

Обычно расходы фаз постоянны по высоте аппарата или мало изменяются. Поэтому, с достаточной для практических целей точностью можно считать, что G_н = G_к = G = const, L_н = = L_к = L = const и уравнение принимает вид:

y = (7.2).

Обозначим L/G = A и 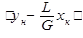= В, получаем у = Ах + В. Таким образом, рабочая линия представляет собой прямую, которая наклонена к оси абсцисс под углом, тангенс которого равен А, и отсекает на оси ординат отрезок, равный В.

Аналогично, для части аппарата от некоторого произвольного сечения до верхнего конца материальный баланс имеет вид G у + L_нх_н = G_ку_к + Lх, а уравнение рабочей линии: y = (7.3).

Выражения (7.2) и (7.3) являются уравнениями рабочей линии, которыми обычно пользуются при расчётах массообменных процессов.

Дата добавления: 2014-12-16